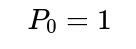ML Interview Q Series: Recurrence Relation for Even Heads Probability in Biased Coin Tosses
Browse all the Probability Interview Questions here.
A biased coin has probability p of landing heads and is tossed n times. Determine a recurrence relation for the probability that the total number of heads obtained after n tosses is an even number.
Short Compact solution
Let A denote the event that the total count of heads after n tosses is even. Consider B to be the event that the first toss is tails, and B′ that the first toss is heads. By the law of total probability:
When the first toss is tails (with probability (1−p)), the event of having an even number of heads depends on the probability that there were an even number of heads in the remaining n−1 tosses.
When the first toss is heads (with probability p), having an even number of heads now depends on the probability that there were an odd number of heads in the remaining n−1 tosses (i.e., the complement of having even).
Hence, the recurrence is given by:
Comprehensive Explanation
Key Observations
Initial Conditions
For completeness, it helps to specify an initial condition. When n=0, we have tossed the coin zero times, and by convention the number of heads is 0—which is even. Hence:
Direct Closed-Form
While the recurrence is enough to answer the question, it can also be solved explicitly. By iterating the relation, one obtains:
This closed-form arises because even/odd can be thought of as a two-state Markov chain in which you “flip” states (from even to odd or odd to even) with probability p when you toss a head, and stay in the same state with probability (1−p) when you toss a tail. The stationary distribution or direct method of solving the recurrence both yield the same expression.
Relevance in Machine Learning
Though this problem appears purely statistical, insights from such recurrences appear in:
Markov Chain approaches: Transition-based probabilities can often be expressed as simple recurrences.
Probabilistic modeling: Understanding how to express the probability of events over sequential experiments is crucial in time-series analysis, hidden Markov models, and Bayesian approaches.
Potential Follow-up Questions
How would you derive the closed-form expression directly without solving the recurrence?
An alternative derivation uses the binomial expansion. The probability of an even count of heads can be summed over binomial terms:
and noticing how substituting x=p and y=(1−p) but then adding and subtracting appropriate terms can isolate even or odd indices, one obtains:
This would compute the probability via the recurrence relation.
Could you explain a deeper link between this recurrence and Markov chains?
When you model “even number of heads” (E) and “odd number of heads” (O) as states, the coin toss transitions you from E to O with probability p and keeps you in E with probability (1−p), or similarly from O to E with probability p and O to O with probability (1−p). This is a two-state Markov chain. The one-step transition matrix is:
where the first row and column correspond to state E, the second to state O. The recurrence formula emerges naturally by analyzing consecutive transitions in such a chain.
What if p=0.5?
When p=0.5, the coin is fair. The recurrence simplifies because (1−2p)=0, leaving:
for all n≥1. Intuitively, with a fair coin, heads and tails are equally likely, so the probability of an even number of heads is exactly 0.5 for all positive n.
How might this relate to generating functions?
One could create a generating function:
Are there any numerical stability concerns with the direct formula for large n?
How to extend this to a multi-headed coin scenario?
If the coin had more than two outcomes (like a die roll or categorical distribution) but we only cared about a certain category (akin to “heads”), we could still treat it as a Bernoulli trial for “the chosen category” vs. “everything else,” with probability p. The analysis would remain identical. If one needed to track multiple categories simultaneously (for instance, the number of times a side of a die appears is even vs. odd), that would require a different combinatorial approach, but the same concept of parity states can still be extended in more complex ways.
All these deeper insights demonstrate the versatility of recurrences and the fundamental ways we analyze sequential probabilistic events in statistics and machine learning.
Below are additional follow-up questions
Does the probability converge to a limit as n grows very large? If so, what is the limit?
How would we approach the problem if p were itself a random variable with a given prior?
Instead of having a fixed p, one can imagine a Bayesian framework where p is unknown and drawn from a prior distribution (e.g., a Beta distribution). In that case, the probability we are interested in becomes:
Eₚ[P(even # of heads | p, n)]
What changes if toss outcomes are correlated instead of independent?
In such cases, the problem might require constructing a more elaborate Markov chain with additional states that reflect the “history” needed to describe the correlation. For example, if the correlation depends only on whether the prior toss was heads or tails, you need a 4-state chain to keep track of both parity (even or odd) and the last outcome. The transitions would become more complex, and the analysis might not yield as neat a closed-form solution. You would typically write down the transition probabilities among those states and then solve for the stationary or transient probabilities of being in an “even” state. If the correlation is more extensive (involving multiple past outcomes), the state space would grow even larger, making the problem more challenging to solve analytically.
What if there is a hidden or time-varying parameter p that changes from toss to toss?
Is there a straightforward way to incorporate partial knowledge or measurement errors in observing heads or tails?
In certain real-world scenarios, you might not observe each toss perfectly. For instance, there could be a small probability q that a head is misread as a tail or vice versa. This complicates the definition of “even number of heads” because your observed count might not match the actual count. To manage this, you’d introduce a “true” count of heads and an “observed” count. The probability that the observed count is even is then a result of convolving the distribution of actual heads with the distribution of observation errors.
One approach is to define a 2D process:
The actual parity of heads (even/odd).
The observed parity (even/odd).
You’d have a 4-state Markov chain capturing both actual toss outcome and observation error. At each toss, the state transitions with probabilities that reflect not only whether a head occurs but also whether that head is correctly observed. This can drastically increase complexity, and you typically rely on matrix multiplication of transition probabilities rather than a simple one-step recurrence. Such an approach might be overkill for typical coin toss scenarios, but it’s relevant if the problem is generalized to real-world sensors or error-prone classification systems.
Could we generalize this to the probability that the number of heads is congruent to a certain value modulo m?
Yes. Instead of focusing on even (m=2, the “remainder 0” class) vs. odd, we might ask for the probability that the total number of heads is k (mod m) for some integer m>2. This is a more general “distribution of counts mod m.” The analysis involves a Markov chain with m states, each state corresponding to the remainder of heads modulo m. A single toss transitions you from state r to:
state r with probability (1−p), because a tail adds 0 to the count of heads,
state (r+1) mod m with probability p, because a head adds 1 to the count.
The transition matrix has a structure where each row has a (1−p) on the diagonal and p in the next column (with wraparound for the last row). You can raise this matrix to the n-th power to find the distribution over remainders after n tosses. For m=2, this reduces precisely to the earlier 2-state Markov chain. For general m, you’d end up with a more involved matrix power or a direct combinatorial approach, but the principle remains the same.
How might we verify or test the recurrence relation in a practical simulation setting?
A strong approach to verify correctness is by simulation:
Choose a bias p and a number of tosses n.
Repeat many independent experiments:
Generate n Bernoulli samples with probability p for heads.
Count how many heads were observed.
Check if that count is even.
Estimate the fraction of trials in which the count is even.
By running large numbers of simulations, you should see the empirical fraction converge around the theoretical probability, thus validating the recurrence. In practice, for large n, you’d see the empirical fraction approach 0.5 unless p=0 or p=1.
Are there any practical use cases where knowing whether the count of heads is even matters?
An example scenario is in cryptographic or security-based algorithms where parity bits are used as simple checksums. If “heads” stands for a 1-bit and “tails” stands for a 0-bit, the parity of those bits is relevant in error detection codes. Another potential application is in puzzle or betting games where payoffs might depend on parity of certain outcomes. While these might seem contrived or small-scale, the underlying math extends to more complex error-correcting or parity-checking systems in digital communications, where the concept of parity (even or odd counts of some event) is used to detect or correct mistakes.
What if we want to find a confidence interval or measure uncertainty around Pn if p is estimated from data?
Can the recurrence fail or produce paradoxical results if we misuse it?
Yes, if we inadvertently violate assumptions or misapply the formula. Examples:
In essence, the recurrence is correct under the assumptions of a biased coin with a fixed p and independent tosses. Violating those assumptions or inputting an incorrect base condition can lead to wrong or nonsensical results.