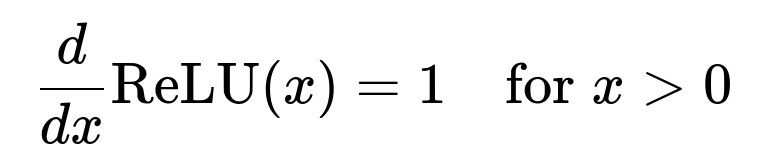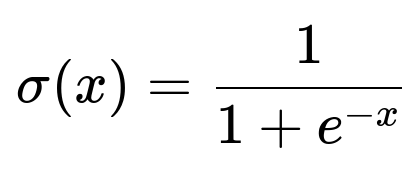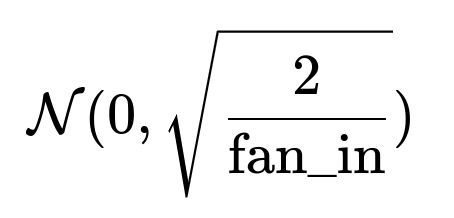ML Interview Q Series: ReLU Activation: Why It Dominates Deep Learning Hidden Layers Over Sigmoid and Tanh.

📚 Browse the full ML Interview series here.

2. Activation Functions (ReLU vs Others): Why is the ReLU activation function often preferred over sigmoid or tanh in hidden layers of deep neural networks? *Discuss the advantages of ReLU (such as alleviating vanishing gradients by not saturating in the positive region) and mention potential drawbacks (e.g., the “dying ReLU” problem), as well as scenarios where other activations might be used.*

ReLU and Its Core Mechanism

ReLU (Rectified Linear Unit) is defined as

ReLU(x)=max⁡(0,x)

This means any negative input is mapped to 0, and any positive input is passed through as-is. Consequently, in the positive region, the gradient is:

and it is 0 when ( x < 0).

When designing hidden layers in deep neural networks, ReLU has certain practical benefits compared to sigmoidal functions (like sigmoid or tanh). Those can be summarized as follows.

Key Advantages of ReLU

Mitigation of Vanishing Gradient

Sigmoid or tanh activations saturate when inputs grow large in magnitude (positively or negatively). In the saturated regions, their gradients approach zero. During backpropagation, these near-zero gradients make it very difficult for weights in lower layers to receive useful error signals, effectively vanishing.

ReLU alleviates this issue by ensuring a constant gradient (equal to 1) for all positive inputs, which allows gradients to propagate back through many layers without becoming exponentially small. This property is crucial for training deeper architectures.

Computational Simplicity

ReLU is computationally cheaper to evaluate because it involves simple thresholding. Sigmoid and tanh require exponentials that can be computationally costlier on resource-constrained systems or large-scale applications. With ReLU, forward passes and backward passes are both straightforward.

Sparse Activation

Because ReLU outputs 0 for negative inputs, a portion of the neurons in any layer can effectively output zeros. This behavior can encourage sparsity. Sparsity can be beneficial in certain contexts, as it may reduce inter-neuron correlation and potentially aid regularization or interpretability.

Potential Drawbacks of ReLU

The “Dying ReLU” Problem

The “dying ReLU” issue emerges when a neuron’s input consistently falls below 0, producing an output of 0. The gradient will also be 0 for those inputs, meaning the neuron’s weights may cease updating. If many neurons get stuck in this state, the network capacity can suffer. For instance, large negative weight updates or high learning rates can cause neurons to enter this regime from which they never recover.

Unbounded Output

While not inherently problematic, ReLU’s output can grow unbounded for large positive values. Sometimes, unbounded activations can cause numerical instability if not managed properly. Techniques such as careful weight initialization and batch normalization mitigate these risks.

Comparison with Sigmoid and Tanh

Sigmoid

Sigmoid is defined by

It is bounded between 0 and 1. This bounded range can be helpful when you need a probability-like output in the final layer. However, when used in hidden layers, the gradient saturates for large positive or large negative ( x). During backpropagation, this quickly leads to vanishing gradients in deeper architectures.

Tanh

Tanh is related to the sigmoid but shifted and scaled: it is zero-centered and maps inputs to ([-1, 1]). Zero-centered nature can help optimization slightly more than sigmoid in some scenarios. However, for large (|x|), tanh saturates and its gradient shrinks toward zero, creating similar vanishing gradient challenges.

Scenarios Where Other Activations Are Preferred

Leaky ReLU / Parametric ReLU

To address the dying ReLU problem, modifications like Leaky ReLU or Parametric ReLU allow a small, non-zero slope for negative ( x). This way, neurons can recover from negative inputs because the gradient is never exactly zero. Example:

$$\text{LeakyReLU}(x) = \begin{cases}

x, & x \ge 0 \ \alpha x, & x < 0 \end{cases}$$ where (\alpha) is a small positive constant (like 0.01).

ELU / SELU

Exponential Linear Units (ELU) or Scaled Exponential Linear Units (SELU) may outperform ReLU in certain architectures, especially self-normalizing networks. They allow negative outputs and can keep activations centered near zero, sometimes helping training converge faster.

Softmax (Output Layer in Classification Tasks)

If the task is classification, the final layer often uses a softmax activation to map logits to probability distributions. But for hidden layers, ReLU-like activations are generally preferred over sigmoidal ones in deep architectures because they avoid saturating behavior and help maintain stronger gradients during training.

Situations Requiring Sigmoid or Tanh

Even though ReLU is widely used in modern deep architectures, there are niche use-cases for sigmoid or tanh:

• Output layer for binary classification: a sigmoid can naturally map to [0,1] for probability interpretation.

• Gating mechanisms in recurrent architectures: gates often use sigmoid or tanh. LSTM or GRU networks rely on these bounded activations to regulate hidden states effectively.

Follow-up Question 1

How does ReLU mitigate the vanishing gradient problem more concretely compared to sigmoid or tanh?

ReLU’s gradient in the positive region is constant and equals 1. With sigmoid or tanh, the gradient can become very small when inputs are large in magnitude, causing updates to diminish exponentially with depth. With ReLU, as long as activations stay in the positive region, the gradient remains a constant 1, helping signals flow backward through the network without being dampened at each layer.

One practical way of seeing this: if we have many layers of neurons using sigmoid or tanh and the inputs to those neurons are large (or very negative), the gradient shrinks rapidly from layer to layer. This means deep networks are extremely difficult to train. ReLU’s piecewise linear shape largely avoids that saturation for positive inputs, making deeper networks more trainable.

Follow-up Question 2

What are effective techniques to reduce the risk of dying ReLUs in a network?

The dying ReLU problem arises when too many neurons shift into the negative regime and receive no gradient. To mitigate:

• Lower the learning rate: A very high learning rate can push weights into regimes where the input to the ReLU is often negative, causing those neurons to “die” rapidly.

• Use careful initialization: Proper weight initialization (for instance, He-initialization for ReLU) helps keep the activations in a reasonable range and reduces the chance of large negative outputs.

• Use Batch Normalization or Layer Normalization: This ensures the distribution of activations remains more stable, reducing the likelihood that many neurons drift into negative territory consistently.

• Use variants like Leaky ReLU: With a small negative slope, even negative inputs have a small gradient, preventing true “death” for those neurons.

Follow-up Question 3

When might sigmoid or tanh be preferable despite their shortcomings?

• Binary classification outputs: Sigmoid is often used in the final layer to produce an output in [0,1], suitable for a probability interpretation when deciding between “yes/no” or “positive/negative” classes.

• Gating mechanisms in recurrent networks: LSTM and GRU networks rely on sigmoidal gates (e.g., forget, input gates) to regulate internal states. Bounded behavior can be beneficial here.

• Certain specialized tasks: Occasionally, tasks that require negative to positive symmetrical outputs or range-bound activation find tanh beneficial. Examples could be autoencoders needing symmetrical outputs or networks that strongly benefit from zero-centered distributions in the intermediate layers.

Follow-up Question 4

Why might we still see tanh or sigmoid in older architectures?

Historical context: Early neural networks often relied on sigmoid or tanh due to their interpretability (probabilistic outputs), the analogy to biological neurons, or simply because ReLU was not popularized until much later. Researchers also used these saturating activations in shallow networks, where vanishing gradients were less critical. With deeper networks, ReLU and its variants superseded sigmoid and tanh in hidden layers because they accelerate training and help alleviate vanishing gradients.

Moreover, certain tradition-bound fields (like some older NLP or speech models) used tanh or sigmoid-based recurrent units. Modern architectures still sometimes incorporate those for backward compatibility or domain-specific preferences, though ReLU or its variants have broadly replaced them in many cutting-edge networks.

Follow-up Question 5

Is the choice of activation function entirely problem-dependent, or are there universal best practices?

Some rules of thumb:

• General-purpose feed-forward layers: ReLU or variants (LeakyReLU, ELU, SELU) are favored for most deep neural networks due to consistent strong gradient propagation.

• Recurrent architectures: Gating activations (sigmoid/tanh) are standard inside GRU and LSTM cells. However, ReLU can appear in separate feed-forward parts of the network, or in certain carefully designed recurrent units.

• Final layer: Often problem-specific. For classification, a softmax or sigmoid is typical. For regression, a linear output might suffice. For tasks that require outputs in a certain range, sometimes a tanh or custom bounded function is used.

In practice, many deep learning frameworks default to ReLU because it works well in broad scenarios. However, real-world tasks might demand refined experiments with activation variants. There is no one-size-fits-all rule, but ReLU-based architectures are almost always the first choice for hidden layers.

Follow-up Question 6

Could the unbounded nature of ReLU cause exploding gradients, and how do we handle that?

Yes, ReLU being unbounded can, in principle, lead to large output values that propagate backward as large gradients. This phenomenon, however, is more commonly mitigated by:

• Weight Initialization: Using variance-scaling approaches (e.g., He-initialization) that keep the activation magnitudes in a controlled range.

• Normalization Layers: Batch normalization, layer normalization, or group normalization often keep the internal statistics stable, preventing uncontrolled growth.

• Gradient Clipping: In some networks, especially recurrent ones, gradient clipping is used to limit the magnitude of gradients if they become too large.

These techniques ensure that while ReLU is unbounded, it does not typically cause unmanageable exploding gradients in practice—particularly in well-designed architectures.

Follow-up Question 7

What implementation details should we watch out for when switching from ReLU to alternatives like ELU or Leaky ReLU in frameworks like PyTorch or TensorFlow?

Implementation considerations:

• Instantiation: For PyTorch, you can import torch.nn.LeakyReLU or torch.nn.ELU. For TensorFlow/Keras, you can specify activation='relu', activation=tf.nn.leaky_relu or use layers like tf.keras.layers.LeakyReLU(alpha=0.01).

• Hyperparameter Tuning: Leaky ReLU or Parametric ReLU come with a hyperparameter (\alpha). ELU also has parameters controlling the alpha in the negative region. Optimal values might differ depending on your dataset and architecture.

• Initialization and Normalization: Different activations can respond differently to certain initialization schemes. For ReLU or Leaky ReLU, “He normal” or “He uniform” initialization is often recommended. For SELU, “lecun_normal” initialization with no batch norm is sometimes recommended when building a self-normalizing network.

• Empirical Testing: Subtle differences in loss convergence can arise when using different activations. Always measure training and validation metrics to confirm any improvement.

An example in PyTorch:

import torch
import torch.nn as nn

class ExampleNetwork(nn.Module):
    def __init__(self):
        super(ExampleNetwork, self).__init__()
        self.layer1 = nn.Linear(100, 50)
        self.act1   = nn.LeakyReLU(negative_slope=0.01)
        self.layer2 = nn.Linear(50, 10)
        # Optionally no activation or another activation in the final layer
        # e.g., cross entropy typically expects logits or softmax
    def forward(self, x):
        x = self.layer1(x)
        x = self.act1(x)
        x = self.layer2(x)
        return x

When replacing ReLU with ELU, you simply change nn.LeakyReLU(negative_slope=0.01) to nn.ELU(alpha=1.0) or whatever configuration you choose.

Follow-up Question 8

How do we interpret the gradient flow differently in ReLU vs. sigmoid/tanh networks?

• ReLU Networks: They either pass the gradient through unaltered (when ( x > 0 )) or kill it (when ( x < 0 )). This can promote stable gradient flow through deep layers for positive activations but risks “dead” neurons if many inputs are negative.

• Sigmoid/Tanh Networks: They effectively scale the gradient by the derivative of those functions, which can be significantly less than 1 if the input is large or small. Over multiple layers, this scaling can lead to an exponential reduction in gradient magnitude.

Hence, while ReLU networks can preserve gradient magnitudes better (less risk of vanishing), sigmoid/tanh networks tend to saturate both for large positive and negative inputs, causing smaller updates for deeper layers.

Follow-up Question 9

Could combining multiple activation functions in the same network be beneficial?

Yes. It is sometimes advantageous to combine ReLU-based layers with gating layers that use sigmoid/tanh. One example is typical in RNNs or LSTM networks that combine fully connected ReLU-based layers for feature extraction and gating mechanisms (sigmoid/tanh) for state updates.

In feed-forward architectures, combining different types of activation functions within the same network is less common, but certain specialized architectures can do so. For instance, a multi-branch architecture might have different activation paths. However, in standard practice, we usually pick one family of ReLU-like functions for hidden layers unless there is a domain-specific reason to mix them.

Follow-up Question 10

Is there a theoretical perspective explaining why ReLU improved deep learning training so much compared to earlier saturating activations?

From a theoretical perspective, ReLU addresses key issues in gradient-based optimization:

• Linear Region: The positive part of ReLU is essentially linear with slope 1, so backprop gradients pass through many layers with minimal distortion.

• Break in Saturation: Sigmoid/tanh saturate on both ends, which dampens the gradient significantly for large (|x|). ReLU’s zero saturation only happens on one side (negative inputs). Therefore, on average, fewer neurons sit in the saturated regime for typical training data distributions.

Moreover, works in deep learning theory suggest that piecewise-linear networks, like those built with ReLU, can represent a wide variety of complex functions while still preserving relatively simple optimization landscapes. In practice, it is easier to train ReLU-based networks at scale with gradient descent methods.

Follow-up Question 11

Can ReLU be used in recurrent or sequence modeling tasks?

ReLU can be used in recurrent neural networks, but caution is required. Purely ReLU-based RNNs might explode in activation for long sequences. Often, gating architectures (LSTM or GRU) with sigmoid/tanh gates are more stable for long-term dependencies. That said, if sequences are relatively short, or if appropriate gradient clipping and normalization are in place, ReLU-based recurrent blocks can be used. Additionally, some advanced recurrent architectures incorporate ReLUs in feed-forward transformations within each time step, while the gating mechanism remains sigmoid/tanh-based.

Follow-up Question 12

What if a certain portion of the data distribution is negative, causing many ReLUs to output zero—does that hurt performance?

If a large fraction of inputs to ReLU layers is negative, the model might underutilize those neurons. This issue can reduce representation power. In real-world data, inputs often have a distribution around zero, or after batch normalization, they become better centered. Thus, with well-tuned initialization and normalization, the portion of negative values is typically balanced so that many neurons can remain in their “active” region. If data is heavily skewed, it may help to reconsider data preprocessing or use an activation with a small negative slope (Leaky ReLU) to keep gradients flowing even for negative inputs.

Follow-up Question 13

Can ReLU be detrimental in networks that must model very small or subtle signals?

Certain data domains, such as modeling signals around zero or capturing both positive and negative fluctuations precisely, could benefit from an activation that has negative symmetry (like tanh) or a non-zero slope for negative inputs (LeakyReLU/ELU). If you need to capture minute changes around negative and positive values equally, plain ReLU might be too coarse. Networks with purely ReLU hidden layers lose sign information for negative activations, which could be limiting in specialized tasks that rely on negative amplitude signals or symmetrical outputs.

Follow-up Question 14

How is ReLU typically initialized and why?

Common initialization scheme for ReLU-based layers is the “He” initialization (also called Kaiming initialization). It aims to maintain variance of forward-pass and backward-pass signals. Roughly, weights in a fully connected or convolutional layer with a ReLU might be drawn from a normal distribution:

where (\text{fan_in}) is the number of input units to that layer. The factor 2 compensates for the fact that the gradient will be 0 for about half of the negative inputs in expectation, preserving the scale of signals during forward and backward passes. This helps keep the network from exploding or vanishing from the earliest steps of training.

Follow-up Question 15

If ReLU is so effective, why do we need all these variants like LeakyReLU, ELU, and SELU?

ReLU works very well, but it has an inherent drawback in the negative region—once activations go negative, gradients become zero. Variants address the risk of dead neurons and other subtleties:

• LeakyReLU: Adds a small slope (\alpha) for negative inputs, so gradients remain non-zero.

• Parametric ReLU: Learns (\alpha) during training.

• ELU / SELU: Attempt to make negative outputs smoothly saturate with a negative exponential, can keep mean activations closer to zero, and can enhance self-normalizing effects.

In some architectures, these can yield marginally better performance or training stability. But in many real-world applications, plain ReLU with good initialization and normalization remains sufficient.

Follow-up Question 16

Could you share a short practical example in PyTorch comparing ReLU and Tanh in the hidden layers?

Yes, consider a simple classification network:

import torch
import torch.nn as nn
import torch.optim as optim

# Example with a single hidden layer
class ReLUNet(nn.Module):
    def __init__(self):
        super(ReLUNet, self).__init__()
        self.hidden = nn.Linear(20, 10)
        self.relu   = nn.ReLU()
        self.output = nn.Linear(10, 2)  # For a classification with 2 classes

    def forward(self, x):
        x = self.hidden(x)
        x = self.relu(x)
        x = self.output(x)
        return x

class TanhNet(nn.Module):
    def __init__(self):
        super(TanhNet, self).__init__()
        self.hidden = nn.Linear(20, 10)
        self.tanh   = nn.Tanh()
        self.output = nn.Linear(10, 2)

    def forward(self, x):
        x = self.hidden(x)
        x = self.tanh(x)
        x = self.output(x)
        return x

# Data placeholders
X = torch.randn(100, 20)  # 100 samples, each 20 features
Y = torch.randint(0, 2, (100,))  # 100 labels, each 0 or 1

# Choose ReLU or Tanh
model = ReLUNet()  # or TanhNet()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)

for epoch in range(50):
    optimizer.zero_grad()
    logits = model(X)
    loss = criterion(logits, Y)
    loss.backward()
    optimizer.step()
    # Usually you'd track validation accuracy/loss here

In practice, the ReLU version often converges faster. The tanh version can still work, but might show slower training or be more prone to gradient saturation, especially if deeper or not well-initialized.

Follow-up Question 17

Conclusion on ReLU vs Others

ReLU has largely become the default for hidden layers in deep networks because it consistently addresses the vanishing gradient problem, is computationally efficient, and often speeds up training. Its drawbacks, like the dying ReLU problem, are mitigated in practice using well-chosen hyperparameters, weight initialization, or slightly modified activation variants (e.g., LeakyReLU). Meanwhile, sigmoids or tanh are often relegated to output layers or specialized gating functions in recurrent architectures. Nonetheless, every activation function has niche scenarios where it might excel, so thorough experimentation and domain knowledge remain essential for selecting the best activation for a given problem.

Below are additional follow-up questions

How do we handle the scenario where the data distribution might be highly skewed, and a large fraction of inputs to hidden layers are either very large positive or very large negative values?

When a data distribution is skewed, large portions of the inputs might frequently produce either very large positive or very large negative activation inputs. For ReLU, extremely large positive inputs will pass through as equally large outputs, potentially causing large weight updates that lead to instability. Conversely, extremely large negative inputs will be zeroed out, risking large fractions of neurons becoming inactive (or “dead” if they get consistently negative inputs).

One practical safeguard is to apply normalization or standardization so that inputs to each layer are centered closer to zero and exhibit manageable variance. Popular examples include batch normalization, layer normalization, and data preprocessing steps such as z-score normalization or robust scaling (especially if there are many outliers). By doing so, the fraction of extremely large positive or negative values is reduced, keeping the network operating in a more stable regime of the ReLU function.

Another consideration is a careful selection of initial learning rate. Even with normalization, if the learning rate is too high and initial weights produce large negative or large positive signals, many ReLUs can remain in the saturated negative zone or produce overly large outputs on the positive side. A moderate or annealing learning rate can help avoid these extremes.

In real-world situations (e.g., financial data with heavy-tailed distributions, sensor data that might saturate or fluctuate widely), it’s critical to experiment with different forms of data transformations to ensure the model sees a less skewed input distribution. If these measures are not sufficient, exploring ReLU variants with negative slopes (LeakyReLU, etc.) or using advanced normalization layers (e.g., GroupNorm) can provide further stability by allowing small negative gradients or controlling internal statistics more granularly.

Does ReLU have any particular interaction with techniques like dropout, and do those interactions impact vanishing or exploding gradients?

Dropout is a regularization technique where certain neurons are randomly “dropped” (i.e., outputs set to zero) during training to prevent co-adaptation. With ReLU-based networks, dropout can lead to additional sparsity since ReLU itself naturally zeroes out negative inputs. It is possible that if the dropout probability is too high, combined with the ReLU’s zero outputs for negative inputs, the network might encounter too many “dead” neurons during training iterations. This can reduce model capacity and slow learning.

However, in most practical scenarios, dropout and ReLU coexist well because:

1. Dropout encourages redundancy: While ReLU imposes sparsity in terms of negative activations, dropout ensures no single neuron’s activation dominates the representation. That synergy often improves generalization.

2. Vanishing or Exploding Gradients: Dropout does not directly mitigate or exacerbate vanishing gradients (which ReLU already helps avoid on the positive side). However, if the dropout rate is extremely high, the effective signal passing through the network is small, and learning can slow down. This is distinct from truly “vanishing gradients,” but can still hamper gradient flow.

As a best practice, if your network architecture is highly prone to zeroed-out outputs (due to ReLU) or if you see underfitting, you might consider slightly reducing the dropout rate or using a ReLU variant (LeakyReLU) so that negative values still pass some gradient. Additionally, batch normalization often works synergistically with ReLU and dropout, helping maintain stable mean and variance of the activations despite random dropping.

In practice, how do we diagnose if a network is suffering from too many ReLUs being in the negative region (i.e., outputs stuck at zero)?

A practical way to diagnose this issue is to log and visualize the activation distributions in each layer:

1. Activation Histograms: Many deep learning frameworks and experiment management tools can record the distribution of activations for each layer. If the histogram is heavily skewed toward zero for extended periods of training, that layer might have too many negative inputs going into ReLU.

2. Gradient Distributions: If you see a large fraction of gradients being zero or near-zero in many ReLU-based layers, it may indicate that most neurons are not receiving updates because they are consistently negative.

3. Loss Plateau: If the training loss plateaus early with no significant improvement over multiple epochs, one culprit could be that many neurons are “dead,” limiting the network’s expressive power. Of course, other factors such as poor hyperparameters or data issues can also cause plateaus, so you must triangulate with other debug metrics.

In practice, standard tools like TensorBoard (in TensorFlow) or similar logging in PyTorch can give you real-time histograms of layer outputs. If you identify extreme sparsity, you might reduce the learning rate, alter initialization, or use a small negative slope activation. Another approach is to incorporate skip connections (as in residual networks) which help keep gradients flowing even if some layers produce zero outputs.

Are there scenarios where a partial saturation in the negative region might be beneficial, making a ReLU-like function less optimal?

In certain generative models (e.g., VAEs or some GAN architectures), having negative outputs can be beneficial if the model is expected to capture features that require negative values. For example, in a generator network that needs to produce signals with both positive and negative values, forcing all hidden units to be non-negative might reduce the representational richness for negative-valued features.

Additionally, in tasks such as waveform modeling, audio signal reconstruction, or other contexts where negative amplitude is meaningful, a strictly non-negative activation could be limiting. A partially saturating function like ELU or a symmetrical function like tanh could better capture the nature of the signals, though each approach has trade-offs in training stability and gradient flow.

In practice, if your domain inherently requires modeling negative features or symmetrical signals, using ReLU might not be detrimental if the final layers are designed to produce negative values. But some hidden transformations might benefit from a function that does not discard negative inputs entirely.

What are some potential pitfalls when combining ReLU with large kernel convolution layers in CNN architectures?

In convolutional networks, ReLU is frequently used after each convolutional layer. However, when kernel sizes are large (like 7x7 or above), the feature maps can have broader receptive fields, and the scale of outputs can grow quite quickly during training if there is no normalization or careful weight scaling. Potential pitfalls include:

1. Over-saturation in positives: Large convolutions can accumulate significant sums, leading to large positive outputs in ReLU, which can cause larger gradients. If the learning rate and initialization are not set properly, this may lead to training instability or even exploding gradients (though less common than with saturating functions).

2. Many zero-activations: Conversely, certain patterns in data might drive entire large kernel filters to produce negative feature map activations, resulting in a block of zeroed-out outputs. A portion of the network might effectively collapse if this becomes widespread.

Typically, modern CNN architectures address these risks by using smaller kernels (3x3, or a stack of 3x3 layers), implementing skip connections, and applying batch normalization. Residual networks, for example, rely on ReLU but mitigate some of its limitations with skip connections that allow gradients to bypass zero-activated layers.

Can ReLU hamper interpretability in deep networks, compared to bounded or smooth activations?

Interpretability can be affected in various ways:

• Piecewise Linearity: With ReLU, each neuron’s transformation is piecewise linear, which can actually simplify certain interpretability methods (like gradient-based saliency maps) because partial derivatives in the positive regime are straightforward.

• Sparse Activation: Because negative inputs become zero, some interpretability techniques might show many neurons are simply “off” for certain inputs, which can be helpful to identify which neurons are strongly active.

• Smoothness and Gradients: Sigmoidal or tanh functions are smooth and continuously differentiable over the entire input domain, which might make some advanced interpretability methods that rely on local gradient continuity behave differently. ReLU has a kink at zero, which can create abrupt changes in attributions around that point.

In real-world interpretability tasks (like analyzing which image features excite certain neurons), ReLU’s simplicity often makes it more straightforward to attribute certain high-level features to neuron activations. That said, if you need a continuous gradient flow across all input ranges for advanced saliency or manifold-based interpretability methods, you might find that the zero region complicates analysis. Still, in practice, ReLU is not usually singled out as a cause of poor interpretability; the depth and complexity of the network architecture itself is often the bigger challenge.

Does the shape of the input data (e.g., very high-dimensional sparse data) affect the choice between ReLU and other activations?

When dealing with high-dimensional, sparse data (like one-hot vectors or large sparse feature sets in recommendation systems or text-based bag-of-words models), ReLU can be advantageous because:

• Positive Activations: If the input features are mostly non-zero or positive (e.g., counts, presence flags, or TF-IDF features), then ReLU ensures these positive signals propagate.

• Sparse Gradients: ReLU can align well with the inherent sparsity because negative signals are outright zeroed. This might lead to simpler gradient updates in practice.

However, if your features are highly negative or represent deviations from some baseline, you might lose information using ReLU since negative inputs are discarded. In such a scenario, ReLU variants (LeakyReLU, ELU) might retain more nuance from negative inputs. The shape and distribution of the input data also inform how you initialize your weights: if the data is extremely sparse, you may want to ensure the network is capable of learning from those few active features in each sample, which can sometimes be enhanced with carefully chosen initialization and a modest learning rate.

Are there hardware or performance considerations when choosing ReLU vs. other activations?

From a hardware perspective:

• Faster Computation: ReLU is generally faster on most hardware (CPUs, GPUs, TPUs) because it uses a simple elementwise max operation. In contrast, sigmoid and tanh involve exponential calculations that are more expensive.

• GPU Vectorization: ReLU’s piecewise function is highly amenable to parallelization, so it can be efficiently implemented as a fused kernel operation in many deep learning libraries.

• Memory Footprint: Typically, the choice of activation has a minimal effect on the overall memory footprint, but more complicated activations might slightly increase memory overhead if they require storing extra intermediate terms for backpropagation.

In large-scale training (e.g., distributing training across multiple GPUs or machines), ReLU has become almost standard due to its computational simplicity. If you are working on specialized hardware like edge devices or microcontrollers, ReLU is often favored to minimize power consumption and ensure real-time performance. Nonetheless, if your model absolutely requires a different activation function for accuracy or domain-specific reasons, you weigh that cost against potential performance hits. Usually, the performance difference between ReLU and simpler variants (LeakyReLU) is minimal because they are still basic elementwise operations with only a constant factor or two overhead.

How do residual or skip connections interact with ReLU in architectures like ResNet or DenseNet?

In ResNet and DenseNet, each “block” typically involves ReLU activations before or after convolutions, but the key difference is the presence of skip or residual connections that allow gradients to flow around potentially saturating or zeroed-out layers. This synergy reduces the impact of:

• Vanishing Gradients: Even if certain ReLU layers block gradients due to negative inputs, the skip connection provides an alternate path for gradients to flow from deeper layers to earlier ones.

• Dying Neurons: A single layer’s ReLU inactivity is less catastrophic because the network can still pass signals through the skip path, making the overall architecture more robust.

In practice, residual connections have enabled training of very deep networks (e.g., 50, 101, 152 layers) using ReLU without the same risk of vanishing gradients that earlier architectures faced. If ReLU kills many activations in some residual block, the skip connection still carries forward a portion of the input unaltered, so the network can effectively “correct” or “add” representations in higher layers.

Is it possible for ReLU-based networks to learn continuous functions that require negative outputs at intermediate layers?

While ReLU outputs are non-negative, networks are not typically restricted to positive outputs at the final layer because subsequent layers can use trainable bias terms or special final-layer activations to produce negative values if required. For instance, a final linear layer with no activation can output any real number in ((-\infty, \infty)). Thus, the network as a whole can learn continuous functions mapping from an input space to any real-valued range, even though intermediate layers discard negative activations.

An important subtlety: intermediate computations that are strictly non-negative may make learning certain transformations less direct. However, with enough layers, biases, and linear transformations, the network can approximate complex functions effectively. This is theoretically demonstrated by the universal approximation properties of piecewise linear networks. Practically, for tasks that rely heavily on negative intermediate representations, practitioners often adopt LeakyReLU or symmetrical activations. But in many domains (computer vision, typical feed-forward classification tasks), standard ReLU suffices.

How might the training dynamics differ if you only use ReLU in the first few layers and then switch to a different activation in deeper layers?

Using ReLU in the initial layers provides strong gradient flow during early feature extraction. In deeper layers, one might switch to an activation like tanh or an advanced activation if the deeper representations need bounded outputs, zero-centric mapping, or negative values. This can be beneficial, for example, in certain autoencoder architectures where the latent representation is constrained or in tasks requiring specific activation properties near the output.

However, mixing activations can complicate hyperparameter tuning because each type of activation might respond differently to initialization, learning rates, and normalization. For instance, the portion of the network using ReLU might be more stable, but the subsequent portion with a saturating activation might hamper gradient flow if it saturates. It’s essential to monitor training carefully for signs of vanishing or exploding gradients in the deeper layers. Typically, if such a scheme is employed, it’s a deliberate design choice based on domain knowledge (e.g., gating or bounding in the final layers) rather than a random mix-and-match of activations.

Could using ReLU in policy or value networks in reinforcement learning cause any special considerations compared to supervised learning tasks?

In reinforcement learning (RL), policy or value networks often deal with more variable, sometimes non-stationary input distributions (states can shift drastically as the agent explores). With ReLU:

1. Exploding Gradients: As exploration leads to states with very different magnitudes, the network might output large activations in the positive region, causing big gradient jumps. Techniques like gradient clipping or adaptive optimizers (Adam, RMSProp) can help.

2. Dead Neurons: If the policy or value function transitions to states that systematically produce negative net input for specific neurons, those neurons might effectively never update. This can be an issue if the agent seldom visits states that would yield a positive activation for them. Deeper exploration strategies, buffer replay (to see a broader distribution of states), or ReLU variants can alleviate this.

3. Reward Scaling: RL tasks often benefit from scaling or normalizing rewards or advantage estimates so that the network does not see extremely large signals that push it too far into the ReLU positive regime. Normalizing or clipping rewards is a common practice to keep training stable.

In summary, ReLU is still a popular choice in many RL architectures due to its simplicity and gradient propagation benefits, but one must be attentive to reward and state scaling, as well as occasional dead neuron issues if the policy or environment rarely triggers certain neuron activations.

Is there a scenario where internal or hidden-layer sigmoid is still used in modern architectures despite ReLU’s popularity?

While ReLU dominates most feed-forward hidden layers in modern deep learning, there remain specialized scenarios for hidden-layer sigmoid:

• Bottleneck autoencoders: Sometimes, an internal layer (especially in the latent/bottleneck) might use sigmoid if the model is meant to learn a probability-like representation or if the latent dimension is intended to be strictly between 0 and 1 for interpretability or domain-specific reasons.

• Certain feature gating: Beyond recurrent networks, one might embed a small gating mechanism in a feed-forward architecture. For instance, a gating subnetwork might determine if certain features are relevant or not, using a sigmoid to effectively “switch on” or “switch off” certain pathways. This can be more explicit than just letting ReLU zero out negative values.

• Legacy or backward compatibility: Some older codebases or pretrained networks might still rely on hidden sigmoid layers. In large engineering teams, if the current system “just works,” they may not migrate everything to ReLU, especially if performance is adequate, or if the model logic is deeply tied to the assumption of bounded hidden states.

How do activation choices like ReLU factor into gradient checkpointing or memory-saving techniques?

Gradient checkpointing (also known as activation checkpointing) is a technique to reduce memory usage by selectively storing only a subset of intermediate activations, then recomputing them on the fly during backpropagation. The choice of ReLU vs. sigmoid/tanh usually does not change the fundamental feasibility of checkpointing, as it is typically a framework-level feature. However:

• Recompute Cost: The cost of recomputing ReLU is extremely low (just a max operation). For sigmoid or tanh, recomputing can be slightly more expensive due to exponentials. Over many layers, that might modestly impact runtime, though it’s typically a small overhead in the grand scheme of training a deep network.

• Sparsity: If many ReLU outputs are zero, the memory saving from storing sparse tensors might be beneficial in some specialized kernels or hardware. However, standard frameworks don’t always take advantage of sparse representations out-of-the-box. So, the zero outputs don’t typically translate into large memory savings by default.

In general, memory-saving techniques do not strongly dictate the activation function choice, but ReLU’s simplicity can reduce the overhead associated with recomputation or storing partial derivatives.

In networks where interpretability is crucial, do people ever prefer continuous and fully differentiable activations (like softplus) over ReLU?

Yes, softplus (defined as ( \log(1 + e^x) )) is a smooth approximation to ReLU. It doesn’t have the hard zero cut-off but transitions smoothly from negative to positive values, meaning it is differentiable everywhere with no corner at zero. In interpretability contexts or theoretical work where certain proofs require the function to be continuously differentiable, softplus might be preferred:

• Smooth Activation Maps: Some saliency or attribution methods produce more stable or smoother explanations if the activation function does not abruptly change slope at zero.

• Less Dying Neuron Problem: Because softplus never exactly hits zero gradient for negative inputs (though it may become very small), it sidesteps the ReLU “dying” scenario.

However, softplus can be slightly slower to compute than ReLU and might reintroduce mild saturation-like effects for large negative inputs. In real-world practice, it’s a niche choice but does show up in some interpretability or theoretical studies.

Could ReLU hamper the network’s capability to model periodic or oscillatory functions in regression tasks?

Yes, ReLU networks can model periodic functions, but they might need more layers or parameters to do so because each ReLU unit is only piecewise linear. To capture oscillations or periodicity effectively, the network often needs multiple breakpoints introduced by multiple ReLUs. In simpler networks or when data is very periodic, a more directly suited activation (e.g., sine/cosine-based activation or radial basis function networks) can handle periodic signals more compactly.

That said, with sufficient depth and width, a ReLU network can approximate such periodic functions to an arbitrary degree, though it might not be as parameter-efficient as using an activation with inherent periodicity. If your problem domain is heavily periodic (like signal processing or certain physics-based tasks), exploring specialized or partially hybrid architectures could yield better performance or simpler networks.

Do large-batch training regimes (like training on thousands of samples per batch) interact differently with ReLU than small-batch training?

Large-batch training can shift activation statistics and gradient scales. With ReLU:

• Activations: Large batches might average out extreme positive or negative fluctuations, potentially resulting in more stable activation distributions if the data is well-shuffled. However, if the dataset is not well-randomized, large batches could become less representative of the overall distribution, occasionally skewing many ReLUs into positive or negative territory.

• Batch Normalization: BN’s statistics might be more stable with larger batches, making it simpler to maintain a consistent range of ReLU activations. For extremely large batches (e.g., thousands of images), this stability can boost training efficiency.

• Learning Rate Scaling: In large-batch settings, practitioners often increase the learning rate. This can exacerbate the risk of dead neurons if the initial update pushes weights in a way that all inputs become negative for certain neurons. Gradual or adaptive LR scaling (like warmup schedules) can mitigate that.

Overall, large-batch training is primarily about careful hyperparameter tuning (learning rate, momentum, warmup, BN settings). ReLU does not inherently break or excel differently in large-batch regimes compared to small-batch, but the risk of dead neurons or overshooting can be higher if hyperparameters are not well-calibrated.

Does the design of skip-gram or embedding-based networks (e.g., word2vec, embedding layers) interact with ReLU choices in subsequent layers?

When you have an embedding layer (e.g., word embeddings in NLP tasks), these embeddings can contain both positive and negative values, which is often beneficial for representing semantic directions in the embedding space. Once these embeddings feed into deeper layers with ReLU:

• Potential for Dead Activations: If an embedding regularly produces negative signals for certain dimensions, the subsequent ReLU layer will zero them out. This might limit the representational capacity for those tokens unless other embedding dimensions remain positive.

• Embedding Tuning: Typically, the embedding training process itself is somewhat separate from the deeper layers. If your architecture is end-to-end, the network can learn to shift the embeddings so that features are more frequently in the positive domain for ReLU. This might inadvertently reduce the embedding’s interpretability or hamper capturing negative directions.

• LeakyReLU or Linear Layers: Sometimes, people insert a small linear transformation or use a LeakyReLU activation right after the embedding layer to preserve some negative information. This approach can help keep the learned negative directions from being destroyed.

If the NLP model is small or if the negative embedding dimensions are crucial, you may consider allowing a small negative slope activation or skipping the ReLU in the first projection layer after embeddings. But in large-scale NLP with transformers or modern architectures, the norm is multi-head attention combined with layer norms, and ReLU or GELU as the activation. The embeddings adapt during training, and minimal performance issues typically arise due to negative dimension zeroing.

Could ReLU lead to a scenario where the final classifier or regressor is heavily biased or offset due to zeroed intermediate representations?

Yes, especially if an entire subset of features or neurons systematically ends up below zero for a given class or region of the data distribution. The network might learn a bias term in subsequent layers to compensate, pushing the pre-activation sums upward. This compensation can still yield accurate predictions, but at times, it may require the model to use more capacity (by adjusting weights and biases) than if negative activations were allowed to propagate some signal.

In classification tasks, as long as the final layer is fully connected with a bias, the network can shift the overall logit or class score. The real question is whether discarding negative signals earlier might hamper certain fine-grained discrimination. Usually, careful initialization, normalization, and a well-designed architecture keep a balanced flow of positive and negative inputs into each ReLU layer so that the network can learn effectively without large systematic biases. But in edge cases (very skewed data, extremely unbalanced classes), you might see the model needing additional layers or special calibration to handle frequent zero activations effectively.