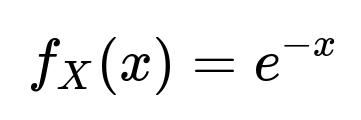ML Interview Q Series: Simulating f(x,y)=e^-y via Exponential Factorization and Inverse Transform Sampling.
Browse all the Probability Interview Questions here.
13E-5. The random variables X and Y have the joint density function f(x, y) = e^-y for 0 ≤ x ≤ y, and 0 otherwise. Describe a method to simulate a random observation from f(x,y).
Short Compact solution
We can factor f(x, y) as f_X(x) f_Y(y|x). By integrating from y = x to y = ∞, the marginal f_X(x) = e^-x for x > 0. Then, f_Y(y|x) = e^-(y - x) for y > x. Hence X ~ Exponential(1) and Y|X=x ~ x + Exponential(1). A sample (X, Y) from f(x,y) can therefore be simulated as follows:
Generate two independent uniform(0, 1) random numbers u1 and u2.
Set x = -ln(u1).
Set y = x - ln(u2).
Comprehensive Explanation
Understanding the joint density
The problem gives a joint density:
with the condition 0 ≤ x ≤ y. Outside this region, the joint density is 0.
Interpreting this setup:
For a particular realization, we must have 0 ≤ x ≤ y.
The factor e^-y suggests an exponential decay in the variable y.
Deriving the marginal distribution of X
To simulate (X, Y) from the joint distribution, we can sample X first from its marginal distribution f_X(x) and then sample Y given X from the conditional distribution f_Y(y | x).
We compute f_X(x) by integrating out y from the joint distribution:
f_X(x) = ∫[y=x to y=∞] f(x, y) dy = ∫[y=x to y=∞] e^-y dy
When we perform this integral: ∫[x to ∞] e^-y dy = e^-x
Thus:
for x ≥ 0, and 0 otherwise. This is precisely the density function of an Exponential(1) distribution (parameter = 1).
Deriving the conditional distribution of Y given X
Next, we find f_Y(y | x) = f(x, y) / f_X(x). From the expression f(x, y) = e^-y and f_X(x) = e^-x, we have:
f_Y(y | x) = e^-y / e^-x = e^-(y - x)
for y ≥ x. Recognizing that y must be greater than x, we can also think of Y as X plus a positive offset. That offset is distributed as an Exponential(1) random variable. Indeed, f_Y(y | x) is an exponential distribution in the variable (y - x) with parameter 1, so:
for y ≥ x.
Putting it all together (simulation steps)
Sample X from Exp(1): Generate a uniform(0, 1) random number u1. Then set x = -ln(u1). This uses the standard inverse-transform method for sampling from an Exponential(1) distribution.
Sample Y given X: Given x, sample Y by generating another uniform(0, 1) random number u2. Because Y|X=x is x + Exp(1), we can simulate Y by y = x + (-ln(u2)) = x - ln(u2).
Equivalently, many references write that as y = x - ln(u2), which is consistent with thinking of (y - x) = -ln(u2).
Hence, (x, y) = ( -ln(u1), x - ln(u2) ).
Practical Python code example
import numpy as np
def sample_XY(n_samples=1):
"""
Generate samples from the joint distribution f(x, y) = e^-y (0 <= x <= y).
Returns: an array of shape (n_samples, 2)
"""
samples = np.zeros((n_samples, 2))
for i in range(n_samples):
u1 = np.random.rand()
u2 = np.random.rand()
x = -np.log(u1) # X ~ Exp(1)
y = x - np.log(u2) # Y|X=x ~ x + Exp(1)
samples[i, 0] = x
samples[i, 1] = y
return samples
# Example usage:
# data = sample_XY(n_samples=5)
# print(data)
This procedure efficiently generates samples that respect 0 ≤ X ≤ Y with the correct exponential relationship.
Possible Follow-Up Questions
How do we verify that 0 ≤ X ≤ Y in every realization?
One simple check is to notice that X is always nonnegative (since Exponential(1) takes values >= 0). Furthermore, Y|X=x is x + Exp(1) which guarantees that Y ≥ x. Hence in all realizations, 0 ≤ X ≤ Y.
Could Y ever be smaller than X if we implement incorrectly?
If we accidentally sample Y as an independent Exp(1) and then just take (X, Y) = (x, y), we might end up with Y < X. To avoid that, we always add the Exponential draw to x, i.e., y = x + Exp(1). That ensures y ≥ x by construction.
Is there an alternative method to generate these samples?
Yes, one can sometimes use acceptance-rejection or other direct transformations. But the factorization and inverse-transform method is the most straightforward here.
What if we want to use a different parameter for the exponentials?
If the exponentials had a general rate parameter λ (instead of 1), the formulas would modify accordingly. X would be Exp(λ), so X = -(1/λ)*ln(u1). Meanwhile, Y|X=x would be x + Exp(λ). The main idea remains the same: factor the joint density, identify the marginal, and then identify the conditional.
Could this approach extend to higher dimensions?
Yes, for certain multivariate distributions where there is a clear way to factor the joint density as product of marginals and conditionals (or in more complex hierarchical models), a similar approach can be used. In higher dimensions, we might use a chain rule factorization f(x1, x2, ..., xn) = f(x1) f(x2|x1) f(x3|x1,x2) ... , and sample step by step.
What happens if the parameter is 0 (for instance, if we had a degenerate distribution)?
If the rate parameter for an exponential distribution goes to 0, that becomes problematic because the exponential distribution cannot have a rate of 0. In practice, we never set λ = 0. If that occurs in a real modeling scenario, we might have a degenerate or improper distribution. We would then re-express the domain or find a different parameterization.
These points ensure that you fully understand why the sampling procedure works, how to implement it, and how to adapt or verify it for slight variations in parameterization or domain constraints.
Below are additional follow-up questions
How can we verify experimentally that the generated samples follow the correct distribution?
One practical method is to collect a large batch of samples and then compare the empirical distribution of those samples to the theoretical distribution. Specifically, you can focus on two checks:
Marginal distribution of X: Since X is supposed to be Exponential(1), you can perform a Kolmogorov–Smirnov test (KS test) to compare the distribution of your sampled X values against the theoretical Exponential(1) cumulative distribution function (CDF). If the p-value of the KS test is sufficiently high, it suggests that the sample distribution does not deviate significantly from the theoretical Exponential(1).
Conditional distribution of Y given X: For a few different binned values of X, you can check that Y - X is also distributed according to an Exponential(1). You would again use a goodness-of-fit test like the KS test on Y - X for each bin of X. This modular approach helps confirm that Y is generated correctly as X plus an exponential random draw.
A potential pitfall is using a small sample size. If the sample size is too low, the goodness-of-fit test might not reliably detect deviations. In real-world scenarios, a thorough simulation study with multiple sample sizes is a good practice to ensure the sampling method is correct.
What happens if we impose a constraint such as X must be greater than some positive constant c?
In that scenario, our joint density might be modified to reflect that X is now only valid for x >= c. We would then need to re-derive the marginal distribution f_X(x) with the new domain c <= x <= y. The normalization would change, and we could not simply use x = -ln(u1) anymore because that represents an exponential distribution starting at 0. Instead, we might use a shifted or truncated exponential distribution. If the domain is shifted or truncated, the inverse-transform method must be adapted to account for the new lower bound c. This means:
Redefine the distribution of X to handle the region x >= c.
Adjust the sampling steps so that X is sampled from a truncated exponential, for instance using the conditional distribution P(X > c).
A major pitfall is forgetting to re-normalize properly, which would cause an incorrect probability distribution. Ensuring the PDF still integrates to 1 over the new domain is essential.
Could incorrect sampling introduce correlation or biases between X and Y?
Yes. In principle, if you mistakenly sample X and Y as independent exponentials without accounting for the constraint Y >= X, you might end up with spurious correlation patterns or distributions that do not reflect the true joint PDF. In that case, Y might be smaller than X in many samples, violating the domain condition. Even if you keep only samples that satisfy Y >= X by discarding others, you effectively perform a rejection sampling with the wrong proposal distribution, which can introduce biases unless carefully handled and normalized.
To avoid these issues, always derive the correct marginal and conditional distributions. The method described (X ~ Exp(1) and Y = X + Exp(1)) ensures no such bias is introduced because it respects the support Y >= X and the exponential tail properly.
Is there a way to sample from this distribution using a rejection sampling framework?
Yes. You can set up a proposal distribution g(x, y) that is easy to sample from and covers the domain 0 <= x <= y. For instance, one might choose a two-dimensional distribution like a uniform on a triangular region or some known distribution that is always greater than or equal to x. Then you compute the acceptance probability ratio f(x, y) / [Mg(x, y)], where M is a constant such that f(x, y) <= Mg(x, y) for all valid x, y. You draw a candidate (x*, y*) from g and accept it with the acceptance probability. If it is accepted, you keep it; otherwise, you reject and resample.
A subtlety arises in choosing M and g(x, y) so that the acceptance rate is reasonable. For a distribution like f(x, y) = e^(-y) on 0 <= x <= y, the factorization approach used earlier is much more straightforward, so rejection sampling is typically less efficient. However, if for some reason you could not factorize the joint PDF easily (or if the geometry of the domain was more complicated), rejection sampling might be an alternate route. One must be careful to ensure every point in the support has a chance to be proposed and that the ratio is properly bounded.
How should we handle floating-point underflow or overflow when computing exponentials for large or small values?
When simulating with exponentials, for large x or y, e^-y might underflow to zero in standard double-precision arithmetic. For extremely small y - x, exponentials might be close to 1, but subtle numerical issues can still arise if the differences are extremely large or small. Potential strategies:
Use software libraries or data types that support extended precision if you expect x or y to be large.
Avoid computing direct exponentials of large negative arguments. Instead, you might keep track of logs where possible. For example, if you only need to compare probabilities, using log probabilities can mitigate underflow or overflow.
In typical machine learning or simulation contexts, if your rates are around 1 or moderate, standard double-precision float is often sufficient. Problems only arise when the domain extends to extremely large values of x or y.
How does this sampling procedure extend if we have a piecewise definition for f(x, y)?
If the joint PDF changes definition in different regions of x and y (e.g., is e^-y in one region and some other function in another region), you can break down the sampling procedure into cases. For instance, you might:
Determine which sub-region is selected based on probabilities of being in each region.
Conditional on the region selected, use the correct factorization or a tailored method (such as inverse-transform or acceptance-rejection) for that region’s PDF.
A pitfall here is failing to partition the total support properly or mixing up the normalizing constants for each region. Each piecewise part needs to be integrated over its domain to ensure correct sampling proportions.
How would you extend the logic to a Markov Chain Monte Carlo (MCMC) setting for more complex distributions?
If the distribution f(x, y) was just one part of a bigger, more complicated model, you might embed these steps in a Metropolis-Hastings or Gibbs sampling framework. For instance, in a Gibbs sampler, if the full conditional for X given Y remains exponential, and the full conditional for Y given X is also exponential (shifted by X), you can cycle through updating X and Y.
An important detail is ensuring that each conditional update correctly samples from the conditional distribution. If the conditionals match the factorized form we derived, the updates become straightforward. The subtlety is that in more general contexts, you might lose this simple factorization, so you would rely on more general MCMC steps, which could require additional acceptance-rejection or numerical integration.
A common pitfall in MCMC is incorrectly implementing transitions in a way that does not preserve the target distribution, leading to biased samples. Hence, verifying the stationary distribution and ensuring detailed balance (if using Metropolis-Hastings) is crucial.
What challenges can arise if we need to generate extremely large numbers of samples in a production environment?
Practical challenges might include:
Performance: Generating millions or billions of samples requires efficient implementations. In Python, repeated calls to high-level random routines might introduce overhead. Vectorized operations with libraries like NumPy can be faster than a pure Python loop.
Parallelization: Spreading the sampling workload across multiple threads or distributed computing environments can speed things up but also introduces synchronization issues. One must ensure that random number generators in different threads/processes are properly seeded to avoid correlated streams.
Memory constraints: Storing a massive number of samples could become infeasible. You might need to stream the generated samples to disk or process them in batches if you cannot hold them all in memory.
Verification: With a large-scale generation, even small mistakes (like an off-by-one domain error) can become very costly in terms of time and compute usage. Thoroughly testing correctness with smaller runs is essential before scaling up.
Potential pitfalls in production might involve incorrectly sharing random seeds across different processes or ignoring the subtle domain condition that y >= x. Thorough design and testing is the best mitigation strategy.