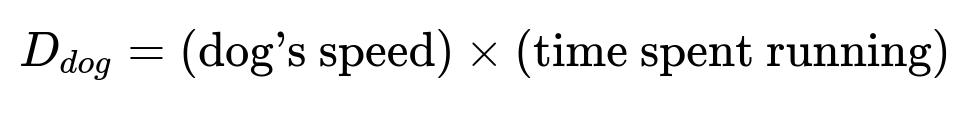ML Interview Q Series: Solving the Back-and-Forth Dog Problem: Total Distance via Time and Speed

Browse all the Probability Interview Questions here.

A man and a dog begin on opposite sides of a 100-foot field. The man runs at x ft/s, while the dog runs at twice that speed. As soon as they start running toward each other, the dog goes back and forth between the man and its own starting end each time it meets the man, continuing until the man reaches the far end of the field. What is the total distance the dog travels by that time?

Comprehensive Explanation

One way to analyze this scenario is to notice that the back-and-forth motion of the dog does not affect the total time it spends running. The main observation is that the dog keeps running at twice the man's speed until the man finishes covering the entire 100-foot distance.

The man runs at x ft/s, so he needs 100 / x seconds to go from his starting point to the far end of the field (the dog's original position). Throughout this time, the dog is continuously running at 2x ft/s.

To find the distance traveled by the dog, we multiply the dog's speed by the time it remains in motion.

Here, D_{dog} is the total distance traveled by the dog. The dog's speed is 2x ft/s. The time it runs is the same time the man needs to reach the far end, which is 100 / x seconds. Substituting these values, we get:

D_{dog} = 2x * (100 / x) = 200 feet.

Hence, the dog covers a total of 200 feet.

Even though the dog is running back and forth, the simplest way to solve the problem is to focus on the total running time rather than the number of trips or direction changes. Summing up each small trip segment would be more complicated, but it would yield the same total distance.

A Different Perspective (Infinite Series Approach)

Some people solve this puzzle by summing the lengths of each back-and-forth leg. The dog first meets the man somewhere in the field, turns around, runs back to its original side, then again meets the man, and so forth. Each leg is shorter than the previous, forming a geometric series. However, the approach using total time and speed is far simpler and avoids any tricky infinite summations.

Potential Pitfalls

One might mistakenly assume the dog's back-and-forth path complicates the calculation and try to sum an infinite series without realizing that time * speed also gives the straightforward answer. Another potential error is to forget the man is moving the entire time, so the dog's meeting points shift.

Example with Numerical Values

If x = 5 ft/s, the man would take 100 / 5 = 20 seconds to cross the field. The dog's speed is 2 * 5 = 10 ft/s, so it runs for 20 seconds at 10 ft/s. The dog’s total distance is 200 feet.

Follow-up Questions

How would the solution change if the man and dog started in different initial positions?

If they began at different distances from each other, you would calculate how long the man takes to reach the final destination from his new starting point. The dog’s total distance would again be its speed multiplied by that total travel time, as long as the dog runs continuously at a constant speed.

What if the dog's speed was not constant?

In that case, you could not simply multiply speed by time. You would need an integral of the dog’s speed function over time. For each small time interval, you would determine the dog’s speed, then sum (integrate) all contributions across the total time until the man reaches the other end.

Could we simulate this in code to verify?

Yes. A Python simulation can be written, updating positions of man and dog in small time steps and reversing the dog’s direction each time it reaches an end or meets the man. The sum of the dog’s distances over all time steps will approximate the theoretical result.

man_speed = 5.0  # ft/s
dog_speed = 2.0 * man_speed
field_length = 100.0

time_step = 0.001
man_position = 0.0
dog_position = field_length
dog_distance_traveled = 0.0
dog_direction = -1.0  # -1.0 means moving towards man initially

while man_position < field_length:
    # Update positions
    man_position += man_speed * time_step
    dog_position += dog_direction * dog_speed * time_step

    # Track dog distance
    dog_distance_traveled += abs(dog_speed * time_step)

    # Check for dog-man meeting
    if dog_direction < 0 and dog_position <= man_position:
        # Dog just met the man
        dog_position = man_position  # align positions
        dog_direction = 1.0         # reverse direction
    elif dog_direction > 0 and dog_position >= field_length:
        # Dog just reached far end
        dog_position = field_length
        dog_direction = -1.0

    # End if man reaches other side
    if man_position >= field_length:
        man_position = field_length
        break

print(dog_distance_traveled)

As you reduce time_step, this simulation will converge on the analytical result (200 ft in the example where man_speed = 5 ft/s).

What if the field length was variable?

If the field length is L feet and the man’s speed is x ft/s, the time taken by the man is L / x seconds. The dog runs at 2x ft/s for the same duration, so total distance is 2x * (L / x) = 2L.

When does an infinite series approach become necessary?

Sometimes, you might be asked to derive the position of each dog turnaround point or the number of times the dog reverses direction. In that scenario, an infinite sum of shorter distances is appropriate. Both approaches should produce the same numerical result, though the time*speed method is more direct.

Below are additional follow-up questions

How would the result differ if the dog had a finite reaction time whenever it meets the man?

If the dog pauses momentarily before turning around (perhaps the dog needs some finite reaction time t_react to change direction), the total distance covered will be slightly less straightforward to calculate. The man’s total time to cross the field would still be 100 / x seconds. However, whenever the dog meets the man, it would waste t_react seconds without covering distance. This reduces the effective time the dog is actually in motion. If the dog meets the man N times, then the dog's actual running time is (100 / x) - N * t_react. In practice, N might be quite large if the dog is very fast. Formally, you'd either estimate how many meetings occur within that crossing time or switch to a simulation-based approach to track exact positions at each moment. A subtlety is that each reaction-time pause slightly changes the meeting schedule, so you’d need to carefully handle that in the calculations or simulation.

A potential pitfall: one might forget that the man is still running during the dog's reaction time. Hence, the man’s progress continues, further reducing the actual window for dog travel.

What if there is a maximum distance the dog can travel before it must rest?

A real-world scenario might include fatigue constraints: the dog can only run a certain number of feet or a certain duration before it must stop to rest. Then the dog’s motion is segmented into alternating running intervals and resting intervals. During resting intervals, the man continues to move forward, which affects how many times the dog and the man meet. To solve this, you would break the dog's travel into segments of active running until it is forced to rest. Summing the distance across these segments until the man finishes crossing would give the total distance.

A subtlety might occur when the dog’s rest period spans the time it would normally meet the man or the far side. You would need to account for the dog’s position at the exact moment it starts resting and at the exact moment it resumes running.

What if the field is not a straight line but a curved path or a circular track?

If the field is not a simple linear path, the meeting points and the direction changes become more complicated. For instance, on a circular track of circumference C, the man might run clockwise at x ft/s, the dog runs at 2x ft/s, and they keep meeting around the track. You would then analyze their angular velocities around the circle and find when the angles coincide. The dog’s distance is still 2x times the total time it keeps running, but the total running time to complete one or more laps might change if the man and dog are effectively “chasing” each other around the circle.

A subtlety arises if you consider which “direction” the dog takes (clockwise or counterclockwise). If the dog always runs the shortest path to the man, the geometry can require more careful analysis of the arc lengths, especially if the man and dog keep switching who is effectively ahead in angular position.

How does air resistance or drag factor change the distance if speeds are high?

If the dog's speed is substantial and air resistance becomes non-negligible, the dog's net speed might decrease over time due to drag. Similarly, the man might be slowed down too. This would mean the speed is no longer constant. You would need to set up a differential equation to capture the velocity change over time based on drag forces, such as F_drag = 1/2 * C_d * rho * A * v^2, where v is velocity. Integrating or numerically simulating over time would reveal the true distance covered until the man reaches the other side.

A subtlety is that the dog and man likely have different drag coefficients or frontal areas, making their speed attenuation different. This can lead to changed meeting schedules, so an iterative or simulation-based approach is usually more straightforward than trying to solve analytically.

What if the dog's speed is direction-dependent?

Sometimes, a real dog might run slower away from its owner, or faster towards the owner. Suppose the dog runs with speed s1 when going to the man and s2 when returning to the starting end. In that situation, you can’t rely on a simple constant speed = 2x for the entire trip. The dog’s total distance would be calculated by segmenting every leg of the journey, noting that each leg duration depends on whether the dog is traveling toward the man or toward the starting end. Summing up all these leg distances until the man reaches 100 feet is more involved, but still finite if you methodically track the times and positions.

A subtlety is that each leg’s length might change because the man is also moving. So you need to consider the relative speeds for each leg to know when and where the dog meets the man.

How does the solution change if the man stops partway and never reaches the dog’s starting end?

If the man stops after running a distance d < 100 feet, then the dog could keep traveling back and forth until it meets the man again. But if the man is no longer moving, eventually the dog will come to a final meeting point with the man, because the dog is still moving. In that case, the total distance the dog travels depends on how many times the dog bounces between the man and the far side. Once the dog meets the man after the man stops, there’s no reason for the dog to continue if the problem states it stops once the man has reached his final location (d, not necessarily the far end). You’d recalculate total time or total back-and-forth segments up until the final meeting.

A subtlety is to clarify the problem constraints: does the dog keep going forever if the man never reaches the far end? Realistically, the puzzle might end as soon as the man decides to stop, meaning the dog’s travel ends on the final meeting. That total distance would typically require analyzing the summation of each leg or a time-based approach if the stopping time is known.

What happens if the man changes his speed mid-run?

If the man accelerates or decelerates partway, the dog's journey segments would no longer be consistent. A straightforward approach would be to break the problem into time slices where the man’s speed is constant over a small interval. Within each interval, you calculate the dog’s position changes. Summing all intervals yields the dog’s total distance. The puzzle becomes more complex, but still solvable using piecewise functions or numerical methods.

A subtlety is whether the dog also adjusts its speed proportionally. If the dog always runs at “twice the man’s instantaneous speed,” you would update the dog’s speed as 2 * (man’s speed) in each small time step. A continuous-time differential equation approach might be needed if speeds change smoothly rather than in discrete steps.

What if collisions are disallowed and the dog cannot cross the man’s path, but must turn around just before meeting?

In reality, the puzzle states the dog “meets” the man. However, if there’s a constraint that the dog must avoid crossing into the man’s personal space by some safe margin, the dog might reverse direction just before physically colliding. This modifies the dog’s turning points by a small offset. You would still track the man’s travel time as 100 / x, but each back-and-forth trip is slightly shorter by that safe margin. The difference in distance covered might be tiny if the safe margin is small, but could be more significant if there’s a larger required distance. A precise calculation would track each turnaround point minus that offset.

A subtlety is that if the man and dog are wide enough (like carrying large equipment), the “safe distance” might be more than negligible, and each meeting interval shortens considerably, thus increasing the dog’s meeting frequency. Again, a piecewise or simulation-based approach is helpful.

What happens if multiple dogs are involved, each running back and forth?

With multiple dogs, each dog could run at a certain speed ratio to the man’s speed, and they might also run among themselves. The problem quickly becomes more complicated. However, for each individual dog, the simplest approach is still: distance = speed_of_that_dog * total_time. If each dog runs until the man finishes crossing, and each dog’s speed is constant, you can sum up each dog’s distance individually. Collisions between dogs or other constraints add complexity, but the underlying principle that total distance = speed * running_time remains valid for each dog.

A subtlety arises if the dogs interact with one another, possibly changing speed or direction upon meeting each other, not just upon meeting the man. Then you must factor in each dog’s new schedule of turnarounds. You can still rely on the total time the man is running, but the path of each dog can become quite intricate.

What if the dog's trajectory is two-dimensional rather than one-dimensional?

In a two-dimensional scenario, the dog might not simply run back and forth in a straight line. Instead, it could run diagonally, or in arcs, to intercept the man. If the dog always aims directly toward the man’s instantaneous position, you get a pursuit curve problem. The dog’s trajectory is a spiral-like path if it’s always chasing the moving man. Solving analytically often involves differential equations describing how the dog’s direction and speed change continuously in response to the man’s position. You may find that the dog still arrives at the man in finite time, but the total distance calculation usually requires integrating the speed over the time.

A subtlety arises because the dog is no longer flipping directions in a discrete manner but continuously adjusting its heading. This is a classic pursuit problem (often referred to as a “chase problem” or pursuit curve). The integral approach or a numeric simulation is most straightforward for these more advanced setups.