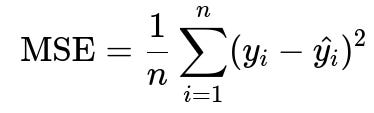ML Interview Q Series: Theoretically correct cost functions may not align with practical business objectives due to simplifying assumptions.​

📚 Browse the full ML Interview series here.

Hint: Mismatch between common proxies like MSE and actual user or business impact

Comprehensive Explanation

A situation often arises where a cost function such as mean squared error seems theoretically sound but may not align with the actual business needs. For instance, in an online retail setting, a model might predict the demand for a product, and one could default to minimizing mean squared error. However, mean squared error focuses on reducing the average squared deviation between the predicted and actual demand values. This might not translate directly into the specific business outcome, which could be maintaining optimal inventory levels, minimizing stock-outs, or reducing carrying costs.

When mean squared error is the cost function, large deviations are heavily penalized because of the squared term, but this does not necessarily reflect how the business incurs costs. A retailer might prefer a slight overestimation (carry a bit more stock) rather than frequent underestimates that lead to stock-outs. The mismatch becomes obvious when your perfectly optimized MSE-based system still causes business losses due to missed sales.

In these scenarios, the solution is to align the mathematical objective with the practical costs or risks encountered by the business. If under-predictions are costlier (lost sales, customer dissatisfaction), you can incorporate asymmetrical penalty terms. Alternatively, if over-predicting leads to perishable goods that become wasted inventory, a different weighting might be more appropriate.

A custom loss function can be designed to factor in the actual monetary loss, or you might adjust the model’s output through post-processing. Both approaches balance the theoretical correctness of model training with the real-world profit or loss considerations of the organization.

Example of a Typical Mismatch

Minimizing mean squared error is mathematically expressed in big h1 font as follows:

Here, n is the number of samples, y_i is the actual target for the i-th sample, and hat{y_i} is the predicted value for the i-th sample. Although MSE is a straightforward proxy to optimize, real costs in many business applications are not simply the squared errors. Business costs may be linear, stepwise, or even asymmetric, depending on whether the prediction is above or below the true value. If a business’s main concern is ensuring they never run out of a product, the true cost of an underestimate is far greater than the cost of an overestimate. Therefore, an MSE-minimizing solution could be suboptimal.

Reconciliation Strategies

One common approach is to incorporate custom loss functions that reflect actual outcomes. For example, if underestimates are more detrimental, you could introduce a higher penalty for negative errors compared to positive errors. Another approach is to use methods like quantile regression, where you can optimize for a high quantile if overestimation is safer or a lower quantile if underestimation is safer. In addition, some businesses create a piecewise cost structure that directly encodes different costs for being above or below the actual target, then embed that into the loss function.

Practical Implementation in Code

Below is a simplified Python snippet to show how you might implement a custom loss that penalizes underestimates more than overestimates.

import torch
import torch.nn as nn

class AsymmetricLoss(nn.Module):
    def __init__(self, alpha=2.0):
        super(AsymmetricLoss, self).__init__()
        self.alpha = alpha  # penalty multiplier for underprediction

    def forward(self, predictions, targets):
        errors = predictions - targets
        loss = torch.mean(torch.where(errors < 0,
                                      self.alpha * errors * errors,  # heavier penalty
                                      errors * errors))
        return loss

# Usage in a training loop
model = ...  # your model
criterion = AsymmetricLoss(alpha=2.0)
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)

for data, labels in dataloader:
    optimizer.zero_grad()
    outputs = model(data)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

This code snippet shows how to weigh negative errors more heavily. If your business needs a different structure, you would modify the condition accordingly.

Follow-up Question: How do you ensure that these custom loss functions are differentiable and still usable for standard optimization algorithms?

Custom loss functions must remain smooth enough so that standard backpropagation can compute gradients. In most frameworks, functions using absolute values, squared terms, or piecewise definitions can be written in a differentiable manner if properly managed. For piecewise definitions that are not differentiable at certain points, frameworks often use subgradient approaches. When designing such a loss function, you ensure that each region of your piecewise definition is differentiable and handle boundary conditions carefully.

Follow-up Question: How do you decide whether to modify the loss function or just do a post-processing adjustment?

You can compare both approaches in terms of training complexity, interpretability, and the level of direct business objective alignment. If the issue is mostly about threshold decisions (for example, you want to push your predictions slightly higher than the raw model output), a post-processing approach might be simpler. If the problem is rooted in the fundamental nature of how predictions are learned, custom losses can provide a more principled approach by allowing the model to learn the relationship that matches the business cost structure.

Follow-up Question: How do you handle scenarios where business impact is dynamic or changes over time?

You can introduce time-varying or context-dependent weighting in the cost function. This might involve adjusting the penalty parameter according to real-time feedback on inventory levels, seasonal factors, or external changes. Another approach is to retrain the model on recent data that reflects the updated business environment, or to maintain a buffer approach that updates the weights used in the loss function as new cost information becomes available.

Follow-up Question: How do you validate that your chosen cost function truly aligns with business metrics?

You can measure performance on actual business outcomes once the model is deployed. For instance, you might look at additional metrics like net profit, customer satisfaction, or stock-out rates. This real-world feedback loop will confirm whether the custom cost function yields the intended impact. A/B testing is also a practical method to observe differences between a baseline model with a standard cost function and the new model that implements the modified objective.

Below are additional follow-up questions

How do you handle sudden distribution shifts in your data that invalidate the chosen cost function?

Sudden distribution shifts occur when the data your model encounters in production looks very different from what it was trained on. An example might be a seasonal retail business that experiences a huge spike in demand during the holidays, while your cost function was tuned under steady-state assumptions.

To address this, you could monitor relevant business metrics in near real time. If those metrics deviate significantly from their historical norms, you can trigger a retraining process with data that reflects these new conditions. Another approach is to develop an adaptive or online learning strategy, where the model parameters are updated more frequently as new data comes in. Additionally, you might consider building ensemble methods that combine models optimized for various seasonal or situational contexts, switching or weighting them depending on indicators of distribution shift.

A subtle pitfall is overfitting to short-term anomalies. If your cost function is heavily penalizing certain errors during a temporary shift, you might inadvertently adapt the model too aggressively, causing worse performance once conditions revert back. Regular validation on both recent data and a broader historical set can help mitigate this risk.

How do you ensure your custom cost function can be interpreted by non-technical stakeholders?

When you move away from standard metrics (like mean squared error) to a more nuanced function that reflects business priorities, non-technical stakeholders might have difficulty understanding how it operates or why it matters. You can address this by breaking down the components of the function in business-language terms. For example, if you have an asymmetric penalty, show them how an under-prediction versus an over-prediction translates into actual dollars lost or saved.

A potential pitfall here is failing to communicate the trade-offs. If you make the cost function heavily penalize underestimates, stakeholders may initially celebrate fewer stock-outs, but they might not expect the corresponding spike in inventory costs from over-predicting. Demonstrating a cost-versus-risk curve can help show the different possible outcomes and enable them to make a data-driven decision about where along the curve they prefer to operate.

How do you handle cases where the business goal is multi-dimensional, and you need to balance conflicting objectives?

In many real scenarios, you might need to simultaneously minimize shipping costs, maximize customer satisfaction, and avoid regulatory fines. These are inherently different metrics that may compete with one another. You could employ multi-objective optimization methods, where you define a combined objective that assigns weights to each component. Alternatively, you might adopt a Pareto optimality approach to find a set of optimal trade-off solutions rather than a single global optimum.

One subtlety is that assigning weights can be political, with different departments wanting their metric to get more emphasis. An iterative approach might be best: start with some initial weighting, measure real business outcomes, and then adjust until you find a balance that most stakeholders can align with. Another complexity is that certain objectives might be hard constraints rather than cost-based. For instance, you might have a “must not exceed” limit for shipping delays. You must handle those constraints separately, potentially through penalty terms or custom validation checks.

What if outliers in your data skew the results of your custom cost function?

Outliers can disproportionately impact standard cost functions, and the same holds for custom ones. For instance, in a demand-forecasting model, occasional “viral” spikes in sales might cause your asymmetrical penalty to explode in value, pushing the model toward consistently high over-predictions, which might not be optimal on average.

A practical mitigation strategy is robust cost functions or data transformations. For example, you might clip or cap predictions beyond a certain percentile if they are likely to be outliers. Another approach is to apply robust regression techniques that reduce the effect of extreme points. But each approach comes with trade-offs. Clipping predictions can ignore genuine surges. Limiting the impact of outliers might reduce your agility in handling sudden legitimate spikes. Therefore, it is crucial to combine domain knowledge with data exploration to decide how to handle these edge cases.

How do you plan for cases where the cost function may be discontinuous or non-differentiable?

Some business-driven objectives create discontinuous or piecewise functions. You might have a steep penalty once inventory shortfalls cross a certain threshold, causing a jump in cost. This is tricky because gradient-based methods rely on smoothness to compute updates effectively.

One strategy is to approximate the discontinuous segments with smoother, continuous curves that still capture the essential penalty pattern but allow the model to be trained with backpropagation. Another technique is to keep the piecewise definition but use subgradient or gradient-free optimization methods (like evolutionary algorithms or specialized solvers) that can handle non-differentiable points. However, these approaches might be slower or more prone to local minima. A careful balance of approximation and domain-specific constraint handling is usually needed to ensure feasibility.

How do you address fairness or bias considerations when designing custom cost functions?

Fairness often comes into play when the decisions your model makes can disproportionately affect certain groups or segments. For example, in a loan approval setting, underestimating default risk for one demographic might lead to losses, while overestimating it for another group might lead to discrimination. If your cost function only targets profit maximization, you might miss these fairness aspects.

To address this, you can incorporate fairness terms directly into your cost function or treat fairness constraints as additional objectives. For example, you might add penalty terms for disparate impact or use fairness metrics such as demographic parity to adjust your model’s outputs. One subtlety is that fairness definitions can vary across legal jurisdictions and ethical frameworks, so you need to be very clear about your definition and keep revisiting it as regulations or public sentiment evolve.

How do you handle organizational inertia when switching from a simple metric like MSE to a more complex business-aligned cost function?

Many teams are familiar with standard metrics such as mean squared error, so transitioning to a custom function may face resistance due to retraining staff, rewriting dashboards, and adjusting established processes. One effective approach is a phased rollout: initially use the custom cost function in parallel with the traditional metric, gather performance evidence, and show how the new approach yields tangible improvements. By demonstrating clear benefits—such as reduced inventory costs, fewer stock-outs, or better user satisfaction—stakeholders become more open to full adoption.

A potential pitfall is implementing a single switch-over without adequately proving value. If you cannot demonstrate early gains, you may undermine trust, and people might revert to old methods. It is also crucial to communicate in a language that resonates with each stakeholder group—finance, operations, marketing—to show that the method addresses their specific KPIs effectively.

How do you scale or maintain performance when your custom cost function is computationally expensive?

Designing a cost function that precisely models every nuance of business costs can lead to a highly complex function that is expensive to compute at scale or for large datasets. This can slow down training, reduce iteration speed, and hinder the team’s ability to experiment and iterate rapidly.

To mitigate this, you can consider approximate methods: maybe a simplified version of the cost function that still captures key aspects but is lighter computationally. You can also look into sampling techniques, using a subset of data that is representative of real-world scenarios, or distributed computing approaches to handle larger data volumes. If your training cycles are extremely long, you risk stalling improvements or missing market changes. Regular monitoring of the training pipeline and the cost function runtime is important to ensure you can sustain iteration velocity over the lifetime of the model.