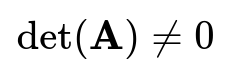ML Interview Q Series: Under which circumstances does a matrix possess an inverse?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
A matrix can be inverted only when certain conditions hold true. The essential aspects include the matrix being square and having a non-zero determinant (among other equivalent conditions such as having full rank). In practical terms, if a square matrix fails any of these criteria, it is termed singular and does not have an inverse.
Square Dimension Requirement
A matrix must be square, meaning it must have the same number of rows and columns. Non-square matrices cannot be inverted in the conventional sense because the concept of a multiplicative inverse in linear algebra is defined only for square matrices. For non-square matrices, techniques like the Moore-Penrose pseudoinverse are used instead, but that is not the same as a true inverse.
Determinant Must Not Be Zero
One of the most fundamental conditions is that the determinant of the matrix must be non-zero. That requirement is often used as the primary test for invertibility.
Here, det(A) is the scalar determinant of matrix A. If this value is zero, the matrix is singular, meaning it does not have an inverse.
Full Rank Condition
Another way to see invertibility is to check the rank of the matrix. An n x n matrix is invertible if, and only if, its rank is n. That means all rows (and columns) are linearly independent. If they are not, there is a redundancy in at least one row or column, causing the determinant to be zero and negating the possibility of an inverse.
Linear Independence of Rows and Columns
An equivalent perspective is that all rows (and columns) must be linearly independent. If any row (or column) can be expressed as a combination of other rows (or columns), the determinant becomes zero. This viewpoint is quite useful when analyzing invertibility through theoretical proofs and geometric interpretations.
Practical Ways to Check Invertibility
In computational practice (for instance, using libraries like NumPy or PyTorch), you can attempt to compute the determinant or directly compute the inverse. When the determinant is very close to zero, numerical instability arises, and the matrix is essentially considered singular in floating-point arithmetic.
Below is an example of how you might check this using NumPy in Python:
import numpy as np
A = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
])
det_A = np.linalg.det(A)
print("Determinant of A:", det_A)
if abs(det_A) < 1e-12:
print("Matrix is essentially singular and not invertible.")
else:
inv_A = np.linalg.inv(A)
print("Inverse of A:\n", inv_A)
In this specific example, the given matrix is singular because its rows are linearly dependent, so the determinant is zero or numerically close to zero.
Why These Conditions Matter
The reason these conditions matter is tied to how we define the inverse. A matrix A is said to be invertible if there exists another matrix B such that A * B = I, where I is the identity matrix. That requirement can only be met if A is square, has a non-zero determinant, and each of its rows (and columns) forms an independent set in a vector space sense.
Potential Pitfalls and Edge Cases
Matrices that are nearly singular (det(A) close to zero) can exhibit numerical difficulties when computing an inverse on a computer. In such scenarios, it is usually better to avoid directly computing the inverse and instead solve systems of equations using other techniques like LU decomposition or other stable methods provided in numerical libraries.
Are Non-Square Matrices Ever Invertible?
Non-square matrices do not have an inverse in the strict linear algebra sense. They can, however, have one-sided inverses or pseudoinverses. These generalized inverses do not fulfill all the properties of a true invertible matrix but can be useful in solving least-squares problems and other optimization tasks.
How Do We Relate Rank to the Determinant?
For an n x n matrix A, if its rank is n (meaning all n rows or columns are linearly independent), then det(A) is non-zero. Conversely, if the matrix has fewer than n linearly independent rows (or columns), the rank is less than n, causing det(A) to be zero. Hence, rank and determinant are intertwined: full rank implies a non-zero determinant, while less-than-full rank implies a zero determinant.
Can a Matrix Have a Non-Zero Determinant and Still Not Be Invertible?
No. For an n x n matrix over a field (like the real or complex numbers), having a non-zero determinant is equivalent to the matrix being invertible. If the determinant is not zero, it automatically implies that the rows (or columns) are linearly independent and that the matrix has full rank.
What If the Matrix is Diagonal?
Diagonal matrices have a determinant equal to the product of their diagonal entries. In that scenario, the matrix is invertible if and only if no diagonal entry is zero. Diagonal invertibility is straightforward to check and to invert: each diagonal element is replaced by its reciprocal in the inverse.
Additional Notes on Numerical Stability
Many real-world problems involve matrices that are large and nearly singular. Even if det(A) is theoretically non-zero, floating-point precision can cause large round-off errors when the determinant is extremely small. In practice, solving systems of linear equations is usually more stable if we rely on factorization methods (like LU, QR, or SVD) rather than explicitly computing the inverse.
Follow-up Questions
What is the geometric meaning of an invertible matrix?
Invertibility can be seen from a geometric viewpoint: a matrix transforms vectors in n-dimensional space. If the matrix is invertible, it implies that the transformation is bijective and does not collapse the space onto a lower-dimensional subspace. In simpler terms, an invertible transformation preserves volume (though possibly rotating or skewing it), but it does not flatten or crush dimensions.
When rank drops, the transformation maps vectors to a space of lower dimension, losing information. From a geometry standpoint, that translates to flattening or shearing in such a way that the overall volume in that n-dimensional space is collapsed to zero, leading to a zero determinant.
Is it always advisable to explicitly calculate the inverse to solve a linear system?
In many practical applications, explicitly calculating a matrix inverse is not optimal due to numerical instability and computational expense. It is more efficient and numerically stable to solve systems of linear equations (for example, A * x = b) by methods such as LU decomposition, QR decomposition, or singular value decomposition. These methods avoid forming the inverse directly.
Does an invertible matrix guarantee it is diagonalizable?
Not all invertible matrices are diagonalizable. A matrix is diagonalizable if it has a sufficient number of linearly independent eigenvectors to form a basis. There are non-diagonalizable matrices that are still invertible. Invertibility and diagonalizability are different properties: invertibility only requires a non-zero determinant, while diagonalizability depends on eigenvalue structure and eigenvector independence.
Could an invertible matrix have complex eigenvalues?
Yes. Even real matrices that are invertible can have complex eigenvalues, especially if they exhibit rotations that cannot be captured by purely real eigenvectors. The presence of complex eigenvalues does not affect invertibility, as long as the determinant is not zero. What matters is that each eigenvalue is non-zero, which ensures the product of all eigenvalues (which is the determinant) is also non-zero.
How does invertibility generalize to other fields or domains?
Most standard discussions use real or complex fields. However, the concept of invertibility is applicable to any field. The determinant concept and rank arguments continue to hold in general fields, meaning that the matrix is invertible if and only if its determinant is non-zero in that field.
All these aspects highlight that the primary condition for matrix invertibility is that it is square and has full rank (equivalently, a non-zero determinant).