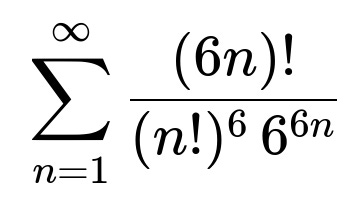ML Interview Q Series: Upper Bound for Probability of Equal Dice Counts Using Union Bound
Browse all the Probability Interview Questions here.
A fair die is repeatedly rolled and accumulating counts of 1s, 2s, …, 6s are recorded. What is an upper bound for the probability that the six accumulating counts will ever be equal?
Short Compact solution
Let A_n be the event that in the first 6n rolls of the die each of the six possible outcomes occurs n times. Then the probability of A_n is
Using the union bound, an upper bound for the probability that the six accumulating counts will ever be equal is the infinite series sum of P(A_n) from n = 1 to infinity. Numerically, this sum is approximately 0.02251. Hence, 0.02251 is an upper bound on the desired probability.
Comprehensive Explanation
The core idea is to use the union bound to assess the probability that, at some point in the sequence of die rolls, all six face counts match exactly. We define the event A_n to be: “After 6n rolls, each face has appeared exactly n times.” Mathematically, the probability of this event is given by the multinomial distribution. The number of ways to arrange exactly n occurrences of each face (1 through 6) in 6n rolls is the multinomial coefficient (6n)! / (n!)^6, and each specific sequence of 6n rolls has probability (1/6)^(6n) for a fair die.
Hence, for any fixed n, the probability P(A_n) is:
where (6n)! / (n!)^6 is the total count of favorable sequences (all six faces appear exactly n times), and 6^(6n) is the total number of possible outcomes for 6n rolls.
To find the probability that the six counts become equal at any roll length 6n for n = 1, 2, 3, …, we consider the event A_1 ∪ A_2 ∪ A_3 ∪ … that any of these “all counts match” events occurs. By the union bound (also known as the Boole inequality), we have:
P(A_1 ∪ A_2 ∪ A_3 ∪ … ) ≤ P(A_1) + P(A_2) + P(A_3) + …
Thus an upper bound for “the six counts are ever equal” is:
When this infinite sum is computed numerically, it converges to approximately 0.02251. Therefore, 0.02251 serves as an upper bound on the probability that, across the entire infinite sequence of rolls, the running tallies of each face value will ever coincide.
Because this is a union bound, the true probability can only be lower (potentially strictly less) than 0.02251. Overlapping events—cases where counts are equal at more than one roll length—make this union bound a conservative estimate.
Why the Union Bound is Used
We rarely can compute the exact probability that a running tally hits equality at some arbitrary time step. The exact probability would require accounting for the possibility that counts become equal at multiple different time steps in an overlapping manner. Summation of P(A_n) directly would double-count such overlaps. The union bound neatly circumvents the complexity of overlaps by providing a simpler, though looser, upper bound.
Possible Follow-up Question: Why is the Actual Probability Strictly Less Than the Sum?
Events A_n can overlap because it is possible for the tallies to be equal at multiple different times. For instance, it is conceivable (though very unlikely) for the counts to be all equal at roll 6n and again at a later roll 6m. When you sum all P(A_n) without correcting for these overlaps, you count those scenarios more than once. Hence the union bound’s sum is strictly an upper bound, so the true probability that the counts ever match is definitely smaller.
Possible Follow-up Question: Could We Estimate This Probability Using Simulation?
Yes, we could perform a Monte Carlo simulation in Python:
import random
import numpy as np
def simulate_equal_counts(num_experiments, max_rolls):
count_success = 0
for _ in range(num_experiments):
counts = [0]*6
success = False
for roll_index in range(max_rolls):
face = random.randint(1,6) - 1
counts[face] += 1
if len(set(counts)) == 1: # all counts are equal
success = True
break
if success:
count_success += 1
return count_success / num_experiments
# Example usage
prob_estimate = simulate_equal_counts(num_experiments=10_000_00, max_rolls=10_000)
print(prob_estimate)
We define a maximum number of rolls (e.g. 10,000) and then count how often the tallies become equal for the first time within those rolls. This is only an empirical approximation, and it will tend to be smaller than 0.02251 for two reasons: (1) We do not roll indefinitely. (2) The true probability can indeed be strictly less than that union-bound threshold.
Possible Follow-up Question: What Happens if the Die is Not Fair?
If the die has different probabilities p_1, p_2, …, p_6 (each p_i > 0, summing to 1), then the probability expression changes. For a specific sequence of length 6n with n occurrences of face i, the probability is p_1^n p_2^n … p_6^n. The combinatorial factor remains (6n)! / (n!)^6, but each sequence’s probability weight is no longer (1/6)^(6n). The union bound approach still applies, though you would sum:
(6n)! / (n!)^6 * (p_1^n p_2^n p_3^n p_4^n p_5^n p_6^n)
across n from 1 to infinity. Numerically computing this sum would again give an upper bound. In most cases (particularly if the probabilities are quite different), the chance of all counts ever matching tends to be even smaller than in the fair scenario.
Possible Follow-up Question: Does the Series Converge for All n from 1 to Infinity?
Yes, the series converges. For large n, the factorial terms grow extremely fast, but so does 6^(6n). Stirling’s approximation can be applied to show that each term decays rapidly. Numerically, the partial sums converge to around 0.02251.
Possible Follow-up Question: Are There Combinatorial or Asymptotic Techniques to Derive a Better Bound?
One might refine the bound using large deviations analysis or methods that account for overlaps in A_n. Some advanced approaches can yield tighter bounds for the probability of seeing equal counts, but those techniques are more involved, often requiring Markov chain methods or more subtle combinatorial arguments. The union bound gives a convenient, straightforward upper bound that is relatively easy to compute.
Possible Follow-up Question: How to Handle Numerical Instability When Computing Factorials for Large n?
For very large n, direct factorial computation (6n)! can be extremely large. Techniques include:
Using logarithms of factorials to sum them before exponentiating.
Employing specialized libraries (e.g., mpmath in Python or arbitrary precision libraries) to compute large factorials accurately.
Using Stirling’s approximation to approximate factorials for large n: log(n!) ~ n log(n) - n + O(log(n)).
All these methods help to stabilize calculations and avoid overflow when n is large. However, since the terms decay quickly, we often only need to sum up to moderate n before the terms become negligible.
Below are additional follow-up questions
Could the counts become equal multiple times during the rolling process?
Theoretically, yes. Although it is highly unlikely, nothing prevents the counts from coinciding more than once. One potential path to multiple equalities might occur if the die rolls produce an early “all counts equal” configuration and then diverge. Later, the randomness of subsequent rolls could cause the tallies to realign again. However, each coincidence event becomes increasingly improbable as the sequence grows, because once the counts diverge (e.g., if one face starts to appear more frequently), it becomes harder for the other faces to catch up exactly in tandem.
Pitfalls/edge cases:
Overlaps make direct probability calculations more complex because one must track joint probabilities of A_n and A_m for n < m.
It is tempting to assume the event of being equal at 6n rolls precludes equality at some later 6m rolls, but this is not necessarily true.
How does the memoryless property (or lack thereof) affect the probability of returning to an equal-tally state?
A single fair die roll is memoryless in that the next outcome does not depend on previous outcomes. However, the count process is not strictly memoryless. Once a particular face gets ahead in its count, it takes a non-trivial sequence of rolls for the other faces to catch up. Even though each roll is independent of the past, the probability of “all counts equal” at a future time depends on how the counts diverged so far.
Pitfalls/edge cases:
One might incorrectly assume that because the die is fair, the chance of returning to equality at any point is the same. In fact, the probability evolves over time, influenced by the current tally distribution.
Markov chain concepts apply to the vector of counts, but the state space is large, making direct Markov chain analysis challenging.
How does the probability of ever reaching equal tallies change if the number of faces is large?
When the number of faces grows, say from 6 to k > 6, the probability of eventually having all counts match typically decreases. Intuitively, with more faces, maintaining an exact balance among them becomes increasingly difficult. The analogous upper bound expression would be:
( kn )! / ( n! )^k * 1 / k^(kn )
for the event that after kn rolls, each face appears exactly n times. Summing over n = 1 to infinity can still be done with the same union bound logic but generally yields a smaller limit as k grows.
Pitfalls/edge cases:
For large k, direct factorial computations become huge, necessitating approximations like Stirling’s formula.
Although the probability decreases with k, the rate of decrease depends on how rapidly ( kn )! grows relative to k^(kn).
Could a large deviations principle give a more precise estimate?
Yes. Large deviations theory can provide asymptotic estimates of rare events like “all faces have the same count.” By looking at how far a multinomial distribution deviates from its typical (central) values, large deviation bounds can tighten the estimate compared to the union bound. However, deriving such bounds can be mathematically involved.
Pitfalls/edge cases:
Large deviations analysis often provides asymptotic statements (n → ∞) rather than exact probabilities for finite n.
Overlaps of multiple events (A_1, A_2, …) can still complicate the direct application of these methods.
How do we ensure that partial sums of P(A_n) capture most of the probability before truncation?
In practice, to get a good sense of the infinite sum, we only sum up to some finite n = N if the terms for n > N are negligible. A straightforward way is to sum terms until they drop below a preset numerical threshold. Alternatively, one can derive an asymptotic bound for the tail of the series, ensuring that the remainder beyond N is very small.
Pitfalls/edge cases:
If you choose N too small, you might cut off significant contributions to the total, underestimating the upper bound.
Factorial computations for large n can lead to overflow or underflow unless handled by a strategy like summing in log-space.
What if we only consider equal tallies after a certain large number of rolls, instead of from the beginning?
Sometimes we might ask: “What is the chance that the counts are equal after, say, 6N rolls for some specific large N?” That would just be P(A_N). But if we wonder about ever being equal from that point onward, we still need a union bound for N, N+1, etc. In that scenario, the event has “missed” earlier chances to be equal, so the probability might be slightly different from the original question starting at roll 0.
Pitfalls/edge cases:
Conditioning on having never been equal before roll 6N complicates the probability analysis. The event of never having been equal so far is not independent of future chances to be equal.
One might over-count or under-count the probability by ignoring how previous rolls shape the count distribution.
How does the distribution of the time at which the tallies first become equal look?
The time of first equality, if it ever happens, is a discrete random variable T ∈ {6, 12, 18, …}. For T to be exactly 6n, we need the event A_n to occur but not A_k for all k < n. The probability mass function (pmf) of T is more complicated than P(A_n) alone because of overlaps among different A_k. Accurately computing P(T = 6n) involves subtracting out cases where the tallies matched at an earlier multiple of 6.
Pitfalls/edge cases:
Attempting to derive a closed-form for P(T=6n) is not straightforward. One cannot merely do P(A_n) − Σ (over k < n) P(A_k) because events can overlap in complex ways (it might be equal at multiple times).
A naive approach might ignore overlaps, leading to an overestimation or underestimation of the pmf.
In a practical setting, does non-stationary behavior of real dice affect the theoretical probability?
Real physical dice might wear down or have small manufacturing imperfections, so over many throws the probability of each face might drift slightly from 1/6. As a result, the actual probability that all tallies align might differ from the idealized 0.02251 bound. Typically, if the bias is not too large, the overall effect remains small, but it can still shift the distribution of outcomes.
Pitfalls/edge cases:
If the bias changes mid-sequence (e.g., the die becomes chipped, or the table surface changes), the process is no longer homogeneous, invalidating the simple i.i.d. assumption.
Real dice rolls with complicated mechanical interactions might have correlations over short sequences (e.g., certain roll patterns repeat if the dice are not well-randomized).
Could partial correlations between faces invalidate the multinomial assumptions?
For a true fair die, each face is independent from one roll to the next. However, if for some reason the die rolls are correlated—say, if outcomes are physically or algorithmically correlated—then the simple multinomial formula for P(A_n) is not strictly correct. You’d have to model the joint probabilities of sequence outcomes under the correlation structure.
Pitfalls/edge cases:
Even minor correlations might accumulate and significantly alter the odds of tallies aligning exactly.
Standard probability tools (multinomial coefficients, union bound) rely on independence across rolls.
What if we require not only that the counts are equal, but also that they are all at least some threshold?
We might modify the question to: “Is there a time when all counts are at least M and exactly the same?” That means we are looking for some n ≥ M such that n occurrences of each face appear. Then the same union bound strategy applies, except n must be at least M. Formally, we look at:
P(∪_{n=M to ∞} A_n).
Pitfalls/edge cases:
The probability might decrease even more because the earliest times (n < M) are disallowed.
Truncating the sum from n = 1 to n = M−1 might neglect a non-trivial part of the event space if M is large.