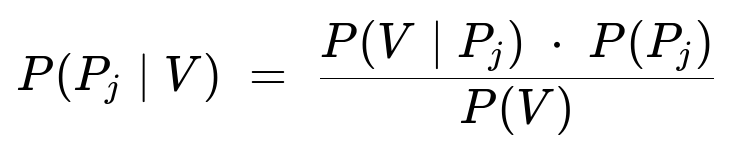ML Interview Q Series: Using Bayes' Theorem to Infer Voter Party Affiliation from Turnout Data.
Browse all the Probability Interview Questions here.
In a certain town, 30% of the people are Conservatives; 50% are Socialists; and 20% are Liberals. In this town at the last election, 65% of Conservatives voted, as did 82% of Socialists and 50% of Liberals. A person from the town is selected at random and states that she voted at the last election. What is the probability that she is a Socialist?
Short Compact solution
We are given:
P(C) = 0.3, P(S) = 0.5, P(L) = 0.2
P(V|C) = 0.65, P(V|S) = 0.82, P(V|L) = 0.5
First compute the overall probability that a randomly chosen person voted:
Using the values: P(V) = (0.65)(0.3) + (0.82)(0.5) + (0.50)(0.2) = 0.705
Then, by Bayes’ Theorem, the probability that the person is Socialist given that she voted is:
Substituting the known numbers: P(S|V) = (0.82 * 0.5) / 0.705 = 0.5816
Hence, there is approximately a 58.16% chance that the person is a Socialist.
Comprehensive Explanation
Bayes’ Theorem allows us to “invert” conditional probabilities. Specifically, when dealing with the question “What is the probability of being Socialist given that this person voted?”, we organize the problem in terms of prior probabilities and likelihoods.
P(C), P(S), and P(L) are prior probabilities of a randomly selected individual being Conservative, Socialist, or Liberal, respectively.
P(V|C), P(V|S), and P(V|L) are the conditional probabilities (likelihoods) that a person voted given their party affiliation.
We want P(S|V), the posterior probability that the person is Socialist given that they voted.
The law of total probability tells us that the overall probability of having voted, P(V), is found by summing the products of each party’s prior probability and its respective likelihood of voting. Concretely:
Among the 30% who are Conservatives, 65% voted. So the fraction of the entire town that are Conservative voters is 0.65 * 0.3 = 0.195.
Among the 50% who are Socialists, 82% voted. So the fraction of the entire town that are Socialist voters is 0.82 * 0.5 = 0.41.
Among the 20% who are Liberals, 50% voted. So the fraction of the entire town that are Liberal voters is 0.50 * 0.2 = 0.10.
Adding these fractions, we get P(V) = 0.195 + 0.41 + 0.10 = 0.705, or 70.5%.
Having P(V), we then apply Bayes’ Theorem to get P(S|V):
P(S|V) = [P(V|S) * P(S)] / P(V)
Here:
P(V|S) = 0.82 is the probability that a person votes given they are Socialist.
P(S) = 0.5 is the prior probability that a person is Socialist.
P(V) = 0.705 is the overall probability that a random person in the town voted.
Substitute: P(S|V) = (0.82 * 0.5) / 0.705 = 0.5816
Thus, the probability is about 58.16%.
Below is a Python snippet showing a quick calculation:
prob_c = 0.3
prob_s = 0.5
prob_l = 0.2
prob_v_given_c = 0.65
prob_v_given_s = 0.82
prob_v_given_l = 0.50
p_v = prob_v_given_c*prob_c + prob_v_given_s*prob_s + prob_v_given_l*prob_l
p_s_given_v = (prob_v_given_s*prob_s) / p_v
print(p_s_given_v) # 0.58156
What if someone asks about interpreting these probabilities in practice?
Bayes’ Theorem in this context means that once we learn a person did vote, we update our beliefs about which party she belongs to based on how likely each party is to vote. Socialists have a higher voting rate (82%) than Conservatives (65%) and Liberals (50%), so given that a person has voted, the likelihood that she is Socialist rises relative to her original 50% chance.
What if the proportions changed?
If the prior probabilities or voting propensities changed, we simply redo the same steps:
Compute the overall probability of voting by multiplying the new party proportions by the new conditional probabilities of voting, then summing them.
Use Bayes’ Theorem with the updated P(V|S) and P(S) to find the new posterior probability.
The method remains identical; only the numeric inputs change.
How would missing information or uncertainty affect this solution?
In real-life scenarios, we might not know the exact voting percentages or exact prior distributions. We might have estimates with confidence intervals. In that case:
We could treat each probability as a random variable with its own distribution and propagate uncertainty through the Bayesian update.
The result would be a distribution over P(S|V) rather than a single fixed number.
How could this be generalized to more than three parties?
The law of total probability generalizes straightforwardly to any finite number of groups. Suppose there are N parties P1, P2, …, PN with probabilities P(Pi), and the probability of voting given party Pi is P(V|Pi). Then:
For the posterior probability of being in party Pj among those who voted:
Are there real-world caveats to using Bayes’ Theorem in voting scenarios?
Bayes’ Theorem mathematically assumes each person’s decision to vote is independent given their party affiliation. In practice, voter turnout might depend on many correlated factors like age, location, campaigning, and current events. However, for an interview or exam-style question, these real-world complications are usually out of scope; the purely mathematical approach is sufficient.
Could this problem be approached in another way?
One alternative is to reason proportionally: out of 100 people,
30 are Conservative, and 0.65 * 30 = 19.5 of those voted.
50 are Socialist, and 0.82 * 50 = 41 of those voted.
20 are Liberal, and 0.50 * 20 = 10 of those voted.
That yields 19.5 + 41 + 10 = 70.5 voters total. Among those 70.5 voters, 41 are Socialists, so 41/70.5 ≈ 0.5816. This is the same result as with the formal probability approach, just using direct counts.
This direct proportional reasoning is often a helpful trick to double-check your Bayes’ Theorem calculations in a more intuitive manner.