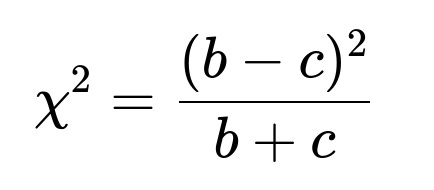ML Interview Q Series: Validating Model Accuracy Gains: Statistical Significance Testing for Comparing Classifiers
📚 Browse the full ML Interview series here.
Statistical Significance in Model Performance: You have two ML models, A and B, and on a test set model A achieved 85% accuracy and model B achieved 87%. How would you determine if model B’s performance is *significantly* better than model A’s and not just due to random chance? *Describe your approach (e.g., hypothesis testing or confidence intervals for the difference in accuracy).*
Below is a comprehensive explanation of how one can rigorously determine if the difference between 85% accuracy (Model A) and 87% accuracy (Model B) is statistically significant, ensuring that any observed improvement is unlikely to be merely random variation.
Deep Conceptual Explanation of the Approach
Hypothesis testing or constructing confidence intervals is the standard way to confirm whether one model’s performance surpasses another’s in a statistically significant manner. By treating the observed accuracies as estimated probabilities of correct classification under each model, we can attempt to quantify the uncertainty around these estimates. Typically, we want to answer the question: Is the difference in accuracy (2%) due to genuine superiority of Model B, or is it within a margin of error that might arise from the randomness inherent in test samples?
Because the same test set is often used to evaluate both models, this raises important considerations. If we simply treat each model’s accuracy independently, ignoring that each individual data point is shared, we risk using an inappropriate statistical test. Ideally, we rely on a paired test that takes into account which examples each model classified correctly/incorrectly.
Below are key ways to perform such an analysis:
Using a Confidence Interval for the Difference in Accuracy
One intuitive approach is to construct a confidence interval for the difference in proportions (proportions of correctly classified samples). Suppose we let:
(p_A) be the true accuracy of Model A on the population (unknown).
(p_B) be the true accuracy of Model B on the population (unknown).
From the test set, we get sample accuracies:
(\hat{p}_A = 0.85)
(\hat{p}_B = 0.87)
The difference is (\hat{p}_B - \hat{p}_A = 0.02) (2%).
If the test set has (n) samples, we can use the standard error for the difference in proportions to construct an approximate confidence interval. However, because the same test set is used for both models, the difference in sample proportions is not fully independent. One recommended approach is:
Let (d_i = 1) if the (i)-th sample is classified correctly by Model B and incorrectly by Model A, (-1) if Model A is correct and Model B is not, and (0) if they both get it correct or both get it wrong.
The sum of (d_i) over all (i) in the test set captures how many additional correct classifications Model B has over A.
This sum and its distribution can be used to compute a standard error or confidence interval on the net difference, factoring in the pairing.
If the confidence interval for (\hat{p}_B - \hat{p}_A) does not include 0 (e.g., if we find that the entire interval is above 0 at some confidence level like 95%), we can conclude that B is statistically significantly better.
Using a Paired Hypothesis Test (e.g., McNemar’s Test)
Another respected method for comparing two classifiers on the same dataset is McNemar’s Test, specifically designed to handle paired data. This test looks at how often each model is correct/incorrect on each test instance:
We form a 2x2 contingency table:
Cell (a): #samples both A and B got correct
Cell (b): #samples A got correct but B got wrong
Cell (c): #samples A got wrong but B got correct
Cell (d): #samples both A and B got wrong
McNemar’s test primarily focuses on b and c—the instances on which the models disagree. Intuitively, if Model B is truly better, you would expect it to outperform A more often (c > b). The test statistic approximately follows a chi-square distribution. For large sample sizes, the standard formula is:
If (\chi^2) exceeds a certain threshold, we reject the null hypothesis (that both models have the same accuracy). A significant result supports that Model B truly outperforms Model A.
Using a Bootstrap Approach
A more computationally intensive but often straightforward approach is to use bootstrapping:
Repeatedly sample, with replacement, subsets from the original test set.
Compute Model A’s and Model B’s accuracy on each resampled subset.
Observe the distribution of the accuracy differences across these bootstrap samples.
Generate the confidence interval of the difference in accuracy by taking suitable percentiles (e.g., 2.5% and 97.5% for a 95% confidence interval).
If that entire bootstrap-based confidence interval of the difference is above 0, we conclude that B’s accuracy is significantly higher than A’s. This approach is flexible and does not rely heavily on theoretical assumptions.
Practical Implementation in Python (Illustrative Example)
Below is a conceptual outline in Python-like pseudocode, focusing on McNemar’s test logic:
import math
from math import comb
from statistics import mean
import numpy as np
def mcnemar_test_predictions(y_true, y_pred_a, y_pred_b):
"""
y_true : array-like of true labels
y_pred_a : array-like of predictions from Model A
y_pred_b : array-like of predictions from Model B
"""
b = 0 # Cases A correct, B wrong
c = 0 # Cases A wrong, B correct
for true_label, pred_a, pred_b in zip(y_true, y_pred_a, y_pred_b):
is_a_correct = (pred_a == true_label)
is_b_correct = (pred_b == true_label)
if is_a_correct and not is_b_correct:
b += 1
elif not is_a_correct and is_b_correct:
c += 1
# McNemar's statistic
chi2_value = (b - c)**2 / (b + c) if (b+c) > 0 else 0
# For large samples, p-value can be approximated with chi-square(1) distribution
# But a continuity correction can also be applied.
return chi2_value
# Example usage:
# Suppose we have arrays of labels and predictions:
y_true = [0, 1, 1, 0, ... ] # ground truth
y_pred_A = [0, 1, 1, 0, ... ] # predictions by Model A
y_pred_B = [0, 1, 1, 1, ... ] # predictions by Model B
chi2_statistic = mcnemar_test_predictions(y_true, y_pred_A, y_pred_B)
print("McNemar's Chi-squared:", chi2_statistic)
If the resulting chi-squared statistic is large enough to surpass a critical threshold, or the derived p-value is below a common significance level (like 0.05), then we conclude B is significantly better.
Why a Simple Difference in Accuracy Might Not Be Enough
Even if Model B’s accuracy is 87% vs. Model A’s 85%, random sampling fluctuations might be the culprit. For example, if the test set is small, a 2% difference might have a wide confidence interval. Alternatively, if the test set is large and the difference remains consistent, it might be a highly robust improvement.
One pitfall is ignoring the correlation between predictions. If we tested the models on different data sets, we could just do a standard difference in proportions test. But because they are tested on the same data, each test sample is effectively “paired,” so we must adjust for that correlation—hence, McNemar’s test or a similar approach.
Addressing Potential Follow-Up Questions
How does sample size influence the detection of statistical significance?
A smaller test set leads to greater uncertainty in estimates of accuracy. A difference of 2% might be large enough to be statistically significant if we had thousands of test samples, but might fail to reach significance with only a few hundred. Generally, the bigger the test set, the smaller the confidence interval and the more sensitive the test is to detect small performance differences.
Does statistical significance automatically imply practical significance?
Even if a difference is statistically significant, it might be too small to matter in a real production environment. For instance, a 0.1% improvement in accuracy might be significant in a huge dataset. One should always consider cost-benefit trade-offs, ease of deployment, computational overhead, and potential user impact in deciding if a difference is practically relevant.
Why would someone use a bootstrap approach over a standard parametric test?
The bootstrap method requires fewer assumptions about the data distribution and can handle complex accuracy metrics (like F1 score, AUC) without requiring specialized formulae. Bootstrapping gives a direct empirical sense of the variability in the performance difference. Parametric tests (like McNemar’s) are well-established, but can hinge on certain assumptions (e.g., large sample counts, or the data fitting certain distributions). Bootstrapping is also conceptually intuitive but more computationally expensive.
What if the dataset is heavily imbalanced? Does that affect these tests?
If the dataset has a severe class imbalance, accuracy might not be the best metric in the first place. One might prefer metrics like precision, recall, or F1 score. To compare such metrics, a suitable statistical test (or a bootstrap approach) could be applied analogously. For instance, if you want to compare F1 scores, you can compute them on resampled data and form confidence intervals or p-values. The same principle of analyzing differences and building confidence intervals applies; just the metric changes.
Can I use a standard t-test for comparing two models?
A plain “two-sample” t-test on the difference of accuracies is generally not correct because each sample (test instance) is evaluated by both models, resulting in a dependency structure. A dependent (paired) test is required. McNemar’s test is effectively a paired test for classification outcomes. If you were comparing average errors across two regression models, a paired t-test could be more appropriate. But for classification accuracy specifically, McNemar’s or a suitable bootstrap test is the standard approach.
How do I interpret the p-value in this context?
A p-value is the probability, under the null hypothesis that “there is no difference between the two models’ performances,” of observing a difference at least as extreme as the one seen. A small p-value (e.g., < 0.05) indicates it’s unlikely that we would see as big a difference in performance if the two models were actually the same. Thus, we reject the null hypothesis and accept that Model B likely has an advantage.
What’s the main difference between McNemar’s test and a confidence interval approach?
They’re closely related in concept. McNemar’s test is a direct hypothesis test that addresses “Is the difference zero or not?” If we wanted an estimate of how big the difference is, along with a margin of error, we’d construct a confidence interval. Both are standard ways of deciding whether the difference is statistically meaningful.
Could you mention a real-world pitfall in applying these tests?
One real-world pitfall is repeated peeking at results. If you keep evaluating your model on the same test set multiple times during iterative development, your test set no longer provides an unbiased estimate of performance. This repeated usage can inflate your chances of finding a “significant” difference by chance. A best practice is to finalize your model choices (e.g., hyperparameters) before performing the final significance test on a truly held-out test set.
How should I handle the case where I have multiple models (more than two) and want to claim one is best?
If multiple pairwise comparisons are performed (e.g., you compare Model A vs B, B vs C, A vs C, etc.), you should adjust for multiple hypothesis testing to control the family-wise error rate (e.g., using a Bonferroni correction) or use a non-parametric multiple comparison test suited for classifier comparisons (e.g., the Friedman test followed by a post-hoc test like Nemenyi). This ensures you don’t incorrectly declare significance because of repeated tests.
Is there a scenario where Model B’s performance appears worse but is still “statistically significantly” better?
This scenario is typically contradictory on the face of it. But one could imagine a scenario with class imbalance and different performance metrics. If B drastically improves performance on a minority class, while having a small drop on the majority class, the overall accuracy might remain lower, yet B might be significantly better in terms of recall or F1 on the minority class. So “better” depends on what metric or hypothesis is tested. In pure accuracy terms, if it appears worse, typically the test would not show significance in favor of B unless some data sampling nuance is at play.
How do you handle randomness when you are training the models themselves?
If the models have random initialization or rely on stochastic gradient descent, you might get different results across multiple runs. In such a scenario, you could measure average accuracy across repeated training runs with different random seeds. Then you could apply a paired statistical test on the results across those seeds (treat each seed as a repeated experiment). Alternatively, for each seed, you collect predictions on the same test set, then check if differences consistently favor Model B. McNemar’s test or a bootstrap approach can be repeated for each pair of final models trained with different seeds, and you examine whether B consistently outperforms A.
Could we directly interpret p-value from the difference in accuracy (like 85% vs 87%) without a formal test?
It’s risky to interpret a direct difference of 2% in raw accuracy as a “p-value.” Different sample sizes and distribution of errors yield different uncertainties. A 2% difference with 100 samples is very different from a 2% difference with 10,000 samples. The formal test is what normalizes for sample size and distributional properties. Without such a test, you can’t be sure if it’s random noise or a genuine difference.
Below are additional follow-up questions
What if the data is sequential or time-based? Does that affect the significance testing approach?
When dealing with time-based (or otherwise sequential) data, each test sample may not be independently drawn from the data distribution. Many of the standard tests for statistical significance (e.g., McNemar’s test, standard difference-in-proportions methods) assume independence between samples. In a time-series setting, autocorrelation in the data can invalidate these assumptions.
For example, if your test examples are consecutive days of stock price movement, each day’s outcome can be correlated with the previous day(s). Because of this, a difference in accuracy (say 85% vs. 87%) may arise from certain temporal patterns rather than a true improvement in classification ability.
One practical adjustment is to apply blocking or batching in time. For instance, you could form blocks of consecutive observations, treat each block as a single unit, and then perform a paired test on these units. Alternatively, you can incorporate a time-series cross-validation approach rather than a standard train–test split, ensuring that the evaluation better respects time order.
Pitfalls might arise if you ignore temporal dependence:
You might incorrectly inflate your sample size (treating each timestep as fully independent), which can lead to falsely low p-values.
Certain performance patterns (e.g., a model that performs well on persistent trends) could appear “significant” if you apply naive tests, yet the advantage might vanish if the trends shift.
So, in time-series scenarios, you must carefully choose a testing strategy that acknowledges potential correlations across time.
How should one handle significance testing for metrics other than simple accuracy (e.g., ranking metrics or multi-label settings)?
Some tasks require specialized metrics beyond plain accuracy:
Ranking tasks (e.g., search relevance) often use mean average precision (MAP), normalized discounted cumulative gain (NDCG), etc.
Multi-label tasks might use subset accuracy, Hamming loss, or an F1-based measure across multiple labels.
The methods behind significance remain similar—construct confidence intervals for metric differences or conduct suitable hypothesis tests—but you need a way to account for dependence among samples or labels. Some approaches:
Bootstrapping becomes highly attractive: you can repeatedly sample from your dataset (or from user queries in a ranking scenario) to approximate the distribution of any performance metric difference. Then you can generate an empirical confidence interval and p-value.
Permutation tests can also be used, especially in ranking tasks, where you randomly shuffle predictions (under the null hypothesis of “no difference”) and check the probability of seeing a difference in your metric as large as the one observed.
Pitfalls and subtleties include:
Different metrics may have different variances. A small difference in NDCG can still be highly meaningful, while a small difference in MAP might be negligible—context matters.
If multi-label data is very sparse (many labels with few positive instances), certain tests might yield unreliable p-values. Ensuring each label has enough support is critical.
Overlapping ground truth across multiple labels can create complex dependency structures that standard tests might not fully capture.
In short, the core idea—quantify the distribution of metric differences and see if zero difference is inside or outside a plausible range—applies universally, but the implementation details vary with the metric’s nature.
What if the test data was used during model selection or hyperparameter tuning?
In an ideal experimental setup, the test set is a purely held-out dataset, never touched during any step of model building or hyperparameter selection. Once you mix test data into hyperparameter tuning, you risk overfitting to the test set, making it an unreliable measure of real performance. This can inflate your observed difference in accuracy or produce artificially small confidence intervals.
Pitfalls in this scenario:
You might repeatedly tweak model B’s hyperparameters based on test performance, eventually beating model A by 2%. However, because you used the test set in the design loop, that 2% advantage might not generalize to truly unseen data.
The concept of “statistical significance” becomes muddy because your test set is no longer an unbiased sample for evaluation. You cannot trust p-values from standard tests if the same data shaped both models in an unequal manner.
The solution is:
Properly separate a development (validation) set or use cross-validation for hyperparameter tuning.
Keep a final test set unseen until the very last evaluation.
If the test set was inadvertently used for tuning, gather a new test set if possible. If that’s not an option, at least be transparent about the potential bias and treat significance claims with caution.
How do we compare significance when one model has a higher median accuracy but also a much larger variance across multiple runs?
In real practice, we often train the same model architecture multiple times with different random seeds (initializations, data shuffling, etc.) and observe the distribution of final performance metrics. Suppose Model A consistently gets around 85% accuracy with a narrow variance (e.g., 84–86%), while Model B on average hits 87% but has a broader variance (e.g., 80–90%).
We can still do a paired comparison of the runs:
For each random seed, you evaluate Model A and Model B on the same test set. This yields pairs of accuracies: (A1, B1), (A2, B2), etc.
You can apply a paired t-test on those final accuracies across seeds (for a large enough sample of seeds). If B’s average is significantly higher than A’s, you might conclude B is better on average.
However, practical considerations can override pure statistical significance:
If B’s variance is so large that in certain runs it dips below A’s typical performance, that might not be acceptable in production.
You might prefer a more stable model (A) to a volatile one (B), especially if high reliability is critical.
Hence, while significance might confirm B’s higher mean performance across many runs, you must also assess risk tolerance for B’s worst-case scenarios. You might also test whether the difference in variability is significant and whether that matters from a business standpoint.
How do missing or partial labels in the dataset affect significance testing?
If the dataset has missing ground-truth labels or partial labeling:
The effective sample size for computing accuracy shrinks to only those instances with known correct labels. This can inflate the variance of your accuracy estimate because you have fewer labeled samples.
Certain statistical tests assume that every sample is labeled (and thus can be counted as correct/incorrect). If you lack labels for some portion of the test set, you may inadvertently skew your test if these unlabeled examples are not missing at random.
Potential pitfalls:
If missing labels correlate with sample difficulty (e.g., the hardest examples remain unlabeled), then your measured accuracies could be overly optimistic, and significance tests can become misleading.
If Model B happens to classify more unlabeled examples (which you cannot confirm as correct or incorrect), you have incomplete information about its real performance.
Practical strategies:
Focus your significance test only on the subset of test samples with reliable labels. This shrinks your sample size but provides more trustworthy outcomes.
Use specialized methods such as partial label learning or weak supervision approaches if partial labels are systematically available. For a significance test, you could measure agreement on fully labeled data and separately analyze partially labeled data with probabilistic confidence intervals.
How should significance be interpreted if the test distribution differs substantially from the training or real-world distribution?
Statistical significance rests on the assumption that the test distribution is representative of the real-world population on which the model is intended to operate. If the test set distribution has shifted (e.g., it’s older data that no longer reflects current conditions), your 2% improvement might not generalize.
Examples of distribution shifts:
A model trained on 2020 email data but tested on 2021 emails might face new spam tactics.
A recommender system tested on last month’s user activity might not reflect the evolving user behavior next month.
Pitfalls:
You may “prove” significance on an out-of-date test set but fail to replicate that advantage in real deployment.
A test set that does not align with current or future conditions might yield stable significance values that do not translate into actual performance.
Solutions:
Continuously monitor data drift. If the real-world data diverges from your test set distribution, you need a new test set or an ongoing evaluation pipeline to keep significance relevant.
Conduct repeated or rolling significance tests using updated data slices, ensuring that the environment is consistent with how you measure performance.
When might a non-parametric approach be more appropriate than a parametric approach for comparing models?
Parametric tests, such as a paired t-test for difference in means, assume the underlying distribution of errors or performance differences meets certain conditions (e.g., normality of differences). Often in classification accuracy, the distribution of differences can be highly discrete and not necessarily normal.
Non-parametric tests, like the Wilcoxon signed-rank test (for paired data) or the sign test, require fewer assumptions. They rely more on ranking or sign patterns in the data rather than a parametric form of the data’s distribution.
Situations prompting non-parametric methods:
If your dataset is relatively small, normality assumptions might not hold.
If your metric is heavily skewed or limited (e.g., accuracy close to 100% for many items, with a long tail for harder items), the distribution is not well-approximated by a normal distribution.
If you are measuring a metric like median absolute error, or if the performance measure has outliers that can disturb standard parametric methods.
Non-parametric tests are robust and reduce the risk of incorrect p-values due to violation of parametric assumptions. However, they can be less powerful than their parametric counterparts if parametric assumptions were satisfied.
How do you handle cases where your test set is very large and even tiny differences end up being statistically significant?
In a scenario with an extremely large test set (e.g., millions of samples), even a 0.1% difference in accuracy can produce a very small p-value, indicating strong statistical significance. However, that difference might not be practically significant if it does not substantially impact user experience or key business metrics.
For instance, an improvement from 85.00% to 85.10% might have a p-value < 0.0001 given a huge test set, even though such a difference might be negligible in practice.
Consider these questions:
Does the improvement justify the additional complexity, computational cost, or model size overhead?
Are there constraints, such as inference speed or resource usage, that overshadow the small accuracy bump?
In such cases, significance can be misleading if interpreted in isolation. You must weigh “practical significance” (cost-benefit analysis, performance constraints) against purely statistical significance. Sometimes you might do an effect size analysis (e.g., Cohen’s d) or treat the difference in more directly interpretable terms (like cost savings, conversions, or user satisfaction scores).
Could significance change if we alter the decision threshold instead of evaluating pure accuracy?
For certain classification models, especially those outputting probabilities (logistic regression, neural networks with a softmax layer, etc.), you can shift the decision threshold to trade off between precision and recall. Accuracy might improve or worsen depending on how you set this threshold.
This interplay can affect significance:
If Model B’s best threshold outperforms Model A’s best threshold by 2%, that might suggest a robust advantage. However, if you fix a threshold at 0.5 for both, maybe the difference is less pronounced.
Model B might be significantly better at certain operating points (e.g., high recall, moderate precision) but not at others. Focusing only on a single default threshold can mask important differences.
You might do a threshold sweep and compare overall performance curves (like ROC or Precision-Recall curves). Then you can use statistical tests on curve-based metrics (e.g., area under the ROC or PR curves) or bootstrap these curves to get confidence intervals. Real-world pitfalls:
Overfitting the threshold to the test set can create the same type of data leakage as using the test set for hyperparameter tuning.
Different thresholds might be relevant in different application domains, so make sure you pick a threshold that aligns with how the model is actually used.
Are there any concerns about repeated comparisons or “cherry-picking” models?
Repeatedly comparing multiple models or multiple variants of the same model can inflate the chance of finding at least one significant difference by random chance alone (the multiple testing problem). For example, if you try 20 hyperparameter variations of Model B and compare each one to Model A with a significance level of 0.05, the probability of at least one false significant result is higher than 0.05.
Strategies to mitigate this risk:
Use a correction method like Bonferroni, Holm-Bonferroni, or Benjamini-Hochberg to adjust p-values for multiple comparisons.
Pre-specify which comparisons are truly of interest before looking at the data to avoid fishing expeditions.
Perform a single global test across all models (e.g., a Friedman test) and then do a post-hoc test only if the global test is significant.
Real-world concerns:
Data scientists might unknowingly (or knowingly) keep tweaking architecture or hyperparameters to try and surpass a baseline. This can lead to “p-hacking,” where eventually you see a “significant” difference by chance.
Documenting your entire search process or using techniques like cross-validation with strict separation can help keep results honest.
What if the test set is tiny due to limited data? Are significance tests still valid?
A very small test set can make it difficult to reliably assess differences in accuracy:
The standard errors become large, making it more likely that the confidence interval for the difference spans zero.
Some tests (like McNemar’s) might be invalid if the number of discordant samples (b + c) is too small.
If your test set is extremely small, practical steps might include:
Using cross-validation, if feasible, to effectively increase the number of test instances. You repeatedly split your data, train on one portion, test on another, and aggregate performance.
Pooling results across multiple small test sets from different time frames or data sources (provided they’re reasonably similar distributions) to build a more robust measure of significance.
Considering a Bayesian approach, where you can incorporate prior information about your model’s expected performance.
However, even with these strategies, if your total labeled data is too limited, strong claims of significance become questionable. Sometimes the best path is to obtain more labeled data or to treat your results as preliminary evidence rather than definitive proof of a difference.
How to interpret and handle significance when using online or streaming evaluation?
In online learning or streaming contexts (e.g., a recommendation system that adapts daily based on new user interactions), model performance can shift over time. Instead of having a single static test set, you gather performance metrics continuously.
You might:
Segment your data stream into consecutive time chunks (e.g., days or weeks). Within each chunk, record Model A’s and Model B’s accuracy. You then have pairs of points (A_t, B_t) over different time periods t.
Apply a paired test (like a paired t-test, Wilcoxon signed-rank, or a bootstrap approach) across these time segments.
Pitfalls:
Non-stationarity: The data distribution might drift, so a significant difference in earlier segments may disappear in later segments.
The number of segments might be small if each segment is large in length, which can reduce statistical power.
If you adapt your models in real time, the definitions of “Model A” and “Model B” might themselves shift, complicating consistent pairwise comparison.
A best practice is to define stable model versions for a fixed period, measure them side by side, then reset your test protocol when you deploy a new version. This ensures a well-defined time window in which significance claims are valid.
How should results be communicated to non-technical stakeholders once significance is established?
Even after confirming that an accuracy difference is statistically significant, many stakeholders care more about real business or user impact than p-values. Communicating effectively is crucial:
Translate the difference in accuracy into an actual impact metric (e.g., “Model B reduces misclassified transactions by 20 per day,” or “Model B yields 10% fewer user complaints”).
Emphasize the concept of confidence intervals or margin of error, so non-technical stakeholders understand that 87% is an estimate, not an absolute truth.
If practical significance is modest, clarify the trade-offs in terms of resource usage, training time, or other cost factors.
Pitfalls:
Overstating statistical significance as if it guarantees guaranteed improvements under all conditions.
Failing to mention that data drift, user behavior changes, or other evolving conditions could reduce that advantage over time.
Not addressing variance or reliability. A single average number can be misleading if the real-world performance is highly variable.
Ultimately, significance is only one dimension of evaluating a model’s readiness for deployment. Ensuring stakeholders understand the uncertainties, assumptions, and real impact fosters more trustworthy model adoption.