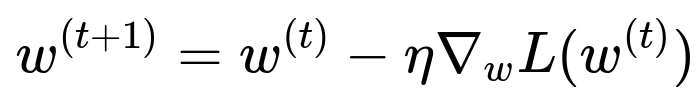ML Interview Q Series: What are some necessary Mathematical Properties a Loss Function needs to have in Gradient-Based Optimization?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

A loss function for gradient-based optimization is a real-valued function mapping from parameter space (for instance R^n) to the real numbers. The fundamental requirement is that this function be amenable to taking a gradient step. This implies several mathematical properties:

Continuity. For standard gradient-based methods, the function must be continuous in the region of interest so that small changes in the parameters do not produce erratic jumps in the function value. Without continuity, any gradient-based approach risks encountering undefined or abrupt changes.

Differentiability (or sub-differentiability). Classic gradient descent relies on computing exact gradients. Hence, one of the most crucial aspects is that partial derivatives exist with respect to each parameter. If the function is not differentiable everywhere, some methods can still cope by using sub-gradients or specialized techniques (e.g., Proximal methods), but in the simplest and most common scenario, we assume differentiability.

Smoothness. In practice, many gradient-based algorithms assume that the gradient does not change too abruptly. Often, it is helpful if the function’s gradient is Lipschitz continuous. Lipschitz continuity of the gradient ensures more predictable behavior of updates and helps with proving convergence rates. While strict Lipschitz continuity is not always mandatory, having a function whose derivatives are not excessively large or unbounded is beneficial for stable and effective gradient-based optimization.

Existence of a Lower Bound. Pure gradient descent methods often need the assurance that the loss function is bounded from below. If the function goes to negative infinity in some direction, then optimization could diverge. Although it is not required to be strictly convex or to have a single global minimum, being bounded from below is generally a reasonable assumption in practical applications (for example, mean squared error is always nonnegative).

Optional Convexity or Quasi-Convexity. Convexity is not strictly necessary for gradient-based optimization to work in practice, especially in deep learning where loss surfaces are highly non-convex. However, in theoretical analyses, convexity or quasi-convexity significantly simplifies convergence proofs and guarantees that local minima are also global minima. In non-convex problems, gradient-based methods can still find local minima or local optima, which may still be acceptable for many real-world applications.

These properties ensure that a gradient-based algorithm can properly compute a search direction and continually refine the parameters to (ideally) minimize the loss.

Central Mathematical Update Rule

One of the most fundamental formulas in gradient-based optimization is the parameter update expression for gradient descent. Although alternative forms exist (like momentum, Adam, RMSProp), the simplest core formula that highlights the necessity of computing gradients is shown below.

Where L(w) is the loss function evaluated at parameter vector w, η is the learning rate, and ∇w L(w^{(t)}) is the gradient of L with respect to w at iteration t. If L is not differentiable or is discontinuous, ∇w L cannot be computed in a straightforward manner, which breaks the standard gradient-based update.

Detailed Explanation of Parameters

Parameter vector w can be in R^n for an n-dimensional model parameter space. L(w) is the scalar loss function we want to minimize. The gradient ∇w L(w) is the vector of partial derivatives of L with respect to each component of w. The learning rate η is a scalar controlling the magnitude of each gradient step. This formula makes it clear that we must be able to evaluate ∇w L(w). Without a proper derivative, the entire scheme of taking small steps in the opposite direction of the gradient cannot be carried out in the usual way.

Follow-up Questions

How does non-differentiability at some points affect gradient-based optimization?

Non-differentiability at certain isolated points does not necessarily prohibit the use of gradient-based optimization. In practical systems (e.g., ReLU activation in neural networks), sub-gradients can be used at those non-differentiable kinks. If the set of non-differentiable points is small, or if sub-gradient methods are employed, optimization methods can still proceed. However, if the function is completely non-differentiable on a large subset, standard gradient-based techniques will not work without modifications.

Sub-gradient methods expand the concept of gradient to a sub-gradient set for convex functions that are not differentiable everywhere. While they can be less stable and slower to converge, they allow optimization to continue around non-smooth regions.

Can gradient-based methods be applied if the function is not convex?

Yes. Gradient-based methods do not require strict convexity. In deep learning, the loss surface is usually non-convex, with many local minima or saddle points. Although there is no guarantee that we will find a global minimum in such scenarios, gradient descent and its variants often produce acceptable solutions. Techniques such as heuristics for initializations, adaptive learning rates, momentum, and batch normalization help navigate complicated landscapes.

Does the loss function have to be strictly positive or bounded?

A loss function does not have to be strictly positive, but being bounded from below is crucial. If the function is not bounded from below, there may be directions in parameter space that lead the function to approach negative infinity, causing divergence. Fortunately, many common losses (e.g., cross-entropy, mean-squared error) are naturally bounded below (e.g., MSE is bounded below by zero).

What is the role of Lipschitz continuity in gradient-based optimization?

Lipschitz continuity of the gradient implies that the gradient does not change too rapidly. This condition helps theoretical proofs of convergence for methods like gradient descent, because it ensures that each step’s update is not too large in unexpected directions. In some references, a function is called L-smooth if it has an L-Lipschitz continuous gradient. While not strictly required for all practical scenarios, it is valuable for establishing step size rules and ensuring stable convergence.

Are higher-order derivatives necessary?

Higher-order derivatives (e.g., the Hessian) are not strictly required for standard gradient descent. They are used in second-order methods such as Newton’s method, which can converge faster under certain conditions but are more computationally expensive and memory-intensive. In deep learning, exact second-order methods are rarely used because of the cost, although approximations (like quasi-Newton or diagonal approximations in Adam) are quite common.

Code Example for a Simple Gradient Descent

import numpy as np

def loss_function(w):
    # Example: simple quadratic function
    return np.sum(w**2)

def gradient_loss(w):
    # Gradient of sum(w^2) is 2*w
    return 2*w

def gradient_descent(initial_w, learning_rate=0.1, iterations=100):
    w = initial_w
    for i in range(iterations):
        grad = gradient_loss(w)
        w = w - learning_rate * grad
    return w

# Example usage
init_params = np.array([1.0, -2.0, 3.0])
optimal_params = gradient_descent(init_params, 0.1, 100)
print("Optimal Parameters:", optimal_params)

In this simplified code, the continuity and differentiability of the chosen loss are evident. The gradient is well-defined and helps direct the parameter updates.

Could we still use gradient-based methods if we only have an approximate or noisy gradient?

Yes. In stochastic gradient descent (SGD), the gradient is estimated using a mini-batch of samples rather than the full dataset, which introduces noise to the gradient estimation. Despite that noise, SGD can still converge, especially when combined with appropriate learning rates and other techniques like momentum or adaptive step sizes. In more advanced settings, one can also employ gradient estimators when the direct gradient computation is not tractable, as long as those estimators approximate the true gradient in a statistically consistent manner.

What if the domain of the parameters is constrained or discrete?

Standard gradient-based methods usually assume continuous parameter spaces. When parameters are constrained or discrete, specialized optimization approaches are used (e.g., projected gradient methods for constrained continuous spaces or gradient-based relaxation techniques for discrete spaces). If the parameter set is entirely discrete with no continuous relaxation, classic gradient descent does not apply directly, since you cannot compute meaningful derivatives in a purely discrete domain.

These considerations reinforce the idea that the fundamental necessity for gradient-based approaches is the ability to compute or approximate a gradient. As long as the loss function is continuous, differentiable (or sub-differentiable), and bounded from below, gradient-based optimization methods can typically operate effectively, with convexity, Lipschitz continuity, and smoothness enhancing theoretical convergence guarantees but not always being strictly required in real-world practice.

Below are additional follow-up questions

What happens if the loss function is piecewise-defined and has multiple non-differentiable boundaries?

A piecewise-defined loss function might contain regions where the derivative is well-defined and regions where it has sharp changes in slope or discontinuities. A classic example is the absolute value function used in L1 losses, which is non-differentiable at zero.

When a function has these boundaries, standard gradient descent can still be applied if we use sub-gradient methods at the boundary points. However, the algorithm might face oscillations around sharp corners because the exact gradient direction can abruptly change. If the boundaries are numerous (e.g., a function composed of many sub-functions), optimization steps may “bounce” between different linear segments.

One subtle pitfall is when many boundaries cluster together. The optimization might get “stuck” if it keeps switching between different sub-gradients without moving significantly in any single direction. Practical mitigation includes:

• Introducing regularization that smooths boundaries (e.g., replacing absolute value with a smooth approximation).

• Using specialized optimization approaches (e.g., proximal methods) if piecewise terms are part of a convex framework.

• Employing adaptive step-size (e.g., Adam) that can handle abrupt gradient changes more gracefully.

How important is step-size scheduling or line search in ensuring stable minimization?

The step-size (learning rate) determines the magnitude of each gradient step. If it is too large, the algorithm may overshoot minima, diverge, or oscillate. If it is too small, convergence can be extremely slow or get stuck near saddle points. Line search algorithms dynamically adjust step-size to find an optimal move along the gradient direction.

The main pitfalls include:

• Fixed step-size that’s not well-tuned can lead to divergence or slow convergence.

• Dynamically shrinking step-size too aggressively might trap the optimizer in a poor local region if the updates become too small to escape.

• For non-convex problems, line search ensures stable movement but does not guarantee finding a global minimum. It merely controls step-size locally.

Real-world complexities like ill-conditioning (where some directions of the parameter space have steeper gradients than others) can make a single global step-size suboptimal. Adaptive optimizers (Adam, RMSProp, AdaGrad) address this by adjusting the effective step-size per parameter dimension based on local gradient statistics.

How do we handle numerical instability when gradients become extremely large or extremely small?

Numerical instability arises when gradients explode (very large values) or vanish (become extremely small). This is common in deep learning with deep architectures, especially when backpropagating through many layers or time steps.

Potential remedies:

• Gradient Clipping. Imposing an upper bound on the gradient norm to avoid excessively large updates.

• Proper Initialization. Using methods like Xavier or Kaiming initialization to keep initial gradients within a reasonable range.

• Normalization Layers. Layer normalization or batch normalization stabilizes activation distributions, helping keep gradients within a moderate scale.

• Residual Connections. In deep networks, skip or residual connections alleviate vanishing gradients by giving direct paths for gradient flow.

A subtle pitfall is that partial fixes like gradient clipping may stabilize training but might mask deeper issues in network architecture or initialization. Continual reliance on gradient clipping without addressing the root cause can lead to suboptimal convergence.

Does the geometry of the parameter space (e.g., manifold constraints) affect gradient-based optimization?

Many machine learning models can have constraints on the parameter space (e.g., orthonormal matrices, positive-definite matrices, or probability simplices). In such cases, the parameters may lie on a manifold rather than the entire R^n space.

When the parameter space is curved:

• Ordinary gradients in R^n are not strictly correct. One must project gradients onto the tangent space of the manifold or use Riemannian gradient descent methods.

• Ensuring parameter feasibility might involve a retraction step that projects an updated parameter guess back onto the manifold.

• Numerical optimization can be more complex since the geometry might have local curvature constraints that standard Euclidean gradient updates do not respect.

An edge case is if the constraints or manifold boundaries create sharp angles or corners—similar to piecewise-defined problems, the algorithm may get stuck near constraint boundaries if not handled properly.

What about “flat” regions or saddle points in the loss landscape, and how do we detect and handle them?

In high-dimensional non-convex landscapes, the model can encounter plateaus (where the gradient is nearly zero for extended regions) or saddle points (points where the gradient is zero but the curvature indicates both increasing and decreasing directions exist).

Common pitfalls include:

• Slow Progress. The model may spend many iterations with negligible progress if the gradient is very small in flat regions.

• Over-Interpretation of Plateaus. One might think the training has converged prematurely when it is merely in a plateau.

Potential strategies:

• Momentum-based Optimizers. They can help accumulate velocity and pass through shallow regions more effectively than vanilla gradient descent.

• Adaptive Methods. Optimizers like RMSProp and Adam adjust the effective learning rate, potentially helping escape flat regions faster.

• Second-order or Quasi-Newton Methods. By approximating curvature, these methods can detect directions of escape in saddle regions. However, their computation can be expensive for large models.

An often-overlooked subtlety is that in very high-dimensional spaces, saddle points might be more common than local minima, leading to repeated slow-down. Practical success in deep learning has shown that well-designed architectures and initializations can often circumvent these issues, though it is not guaranteed.

How do you handle cyclical or periodic objective functions in gradient-based methods?

Some optimization problems involve cyclical structures (e.g., angles in robotics tasks, phase shifts in signal processing, or periodic boundary conditions). A naive parameterization (for instance, directly optimizing angles in R^n) might introduce artificial discontinuities around boundary conditions, such as 0 degrees and 360 degrees actually being the same orientation.

Considerations:

• Re-parameterization. Instead of a single angle parameter, use sine and cosine pairs, which are smoothly differentiable. This removes the artificial discontinuity at 2π.

• Modulo Wrapping. If an angle-based domain is essential, you must handle boundary wrap-around in your gradient steps. Otherwise, you can “jump” across the boundary or produce a large gradient spike near the boundary.

• Topological Awareness. Gradient-based methods in cyclical domains may require knowledge of the manifold structure (a circle, torus, etc.) and ensure that the gradient updates reflect the actual geometry.

If these cyclical patterns are not appropriately accounted for, the optimization can appear to fail or become stuck whenever crossing domain boundaries.

Are gradient-based methods applicable if the loss function changes over time (non-stationary objectives)?

Yes. However, this scenario requires specialized handling, often referred to as online learning or continual learning. The objective or data distribution shifts over time. A few strategies include:

• Online Gradient Descent. Continuously update parameters with the most recent gradient, but older gradient information might become outdated.

• Exponential Forgetting. Gradients from older data are discounted so the optimizer focuses more on the current distribution.

• Meta-Learning. Incorporate knowledge about how the objective changes so that the model can quickly adapt to new conditions.

One subtle problem is “catastrophic forgetting,” particularly in neural networks. When the objective changes, newly updated gradients overwrite previously learned representations. Methods like replay buffers, parameter regularization, or architectural expansions can mitigate this. Stability-plasticity trade-offs become crucial in scenarios where the environment or task distribution is non-stationary.

How do we deal with multi-objective or multi-task learning where multiple losses must be optimized simultaneously?

In multi-objective or multi-task learning, we combine several loss functions into a single scalar objective or optimize them jointly. Typically, a weighting scheme is used, or a more sophisticated approach defines a Pareto frontier.

Potential pitfalls:

• Inconsistent Gradient Directions. Different tasks may require contradictory parameter adjustments, causing frequent oscillations.

• Finding a Good Weighting Strategy. Predefined static weights for each task might not reflect their relative difficulty or importance, leading to under- or overfitting one task at the expense of another.

• Adaptive Task Balancing. Methods that learn optimal weights or use gradient-based approaches to reconcile contradictory objectives are often more robust (e.g., gradient surgery techniques that minimize interference among tasks).

The main subtlety is that even if each individual loss function is differentiable and bounded from below, combining them might produce a more complicated surface. Conflicts between tasks may lead to saddle points or shallow minima that hamper training.

Does stochasticity in the loss function or gradient estimates (beyond standard mini-batches) pose unique challenges?

Yes. Sometimes the loss function itself might be stochastic (e.g., in reinforcement learning, where a reward signal contains inherent randomness or partial observability). Beyond standard mini-batch SGD, the gradient might be an unbiased but noisy estimate of the true gradient.

Key challenges include:

• High Variance. If the gradient estimates have large variance, convergence may be slow or unstable.

• Exploration vs. Exploitation. In reinforcement learning, you must ensure sufficient exploration to gather representative gradient signals.

• Advanced Variance Reduction. Techniques like policy gradients with baseline functions, or importance sampling, try to reduce gradient variance.

A nuanced issue arises when random noise in the loss function is non-stationary, so the gradient changes distribution over time. Algorithms must be robust to these shifts, or they risk overfitting to outdated gradient estimates. Adaptive and variance-reduced methods (e.g., SAG, SVRG) help address these challenges, albeit at additional computational cost.

What if our loss function is not expressed in a closed form but is only accessible via simulations or black-box evaluations?

Sometimes the loss is known only through expensive or noisy simulations. Direct gradient computation might be impossible. Surrogate-based or gradient-free methods like Bayesian optimization or evolutionary algorithms can be used, but these are no longer standard “gradient-based” methods.

However, if one can approximate gradients (for example, using finite differences or policy gradient estimators in RL), then standard gradient-based frameworks can still be applied to some extent. Pitfalls include:

• Computational Overhead. Finite-difference approximations require multiple evaluations of the simulation for each parameter dimension, which can be expensive.

• Inaccurate Gradient Estimates. Noise in simulations can skew the finite-difference or sampling-based gradient estimate, slowing convergence.

A subtle challenge is ensuring the approximation method remains numerically stable. If the simulation output is very noisy or extremely sensitive to parameter changes, the finite-difference gradient can become uninformative.

How do we incorporate constraints (like linear or inequality constraints on parameters) while preserving the differentiability needed for gradient-based methods?

In many real-world scenarios, parameters must satisfy constraints, such as positivity, boundedness, or linear inequalities. Incorporating these constraints requires:

• Projected Gradient Methods. After a gradient step, parameters are projected back to the feasible region. If the projection operation is differentiable almost everywhere, the core approach remains valid, though at the boundaries one might use sub-gradients.

• Barrier or Penalty Functions. Add terms to the loss function that heavily penalize violation of constraints. This can transform a constrained problem into an unconstrained one, but care is needed to avoid ill-conditioning if the penalty is very large.

• Lagrange Multipliers. For more complex constraints, methods leveraging dual formulations or augmented Lagrangian frameworks can maintain differentiability.

An edge case is when constraints partition the domain into multiple disconnected sets. The optimizer may get stuck in a subset containing a local minimum that is not globally optimal across all feasible sets. Proper initialization or multi-start strategies can help explore various feasible regions.