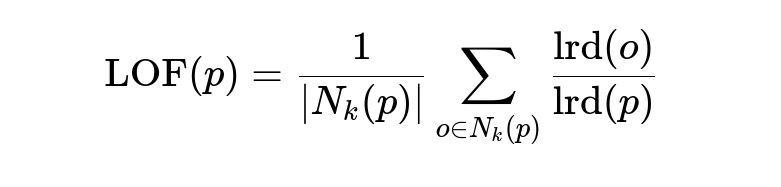ML Interview Q Series: What are the major drawbacks encountered by density-based anomaly detection methods?
Comprehensive Explanation
Density-based anomaly detection algorithms often assume that normal data points occur in dense neighborhoods, whereas anomalies emerge in low-density regions of the data space. One well-known representative is the Local Outlier Factor (LOF) algorithm, which determines how “isolated” a point is compared to its neighbors. Although these methods can be quite intuitive, they come with several limitations.
Challenges with high-dimensional data In high-dimensional spaces, it is extremely difficult to define meaningful densities because distances between points tend to become less distinct as dimensions increase. This phenomenon is sometimes referred to as the “curse of dimensionality.” As a result, density-based methods often fail to accurately identify anomalies in high-dimensional datasets, since the notion of “local neighborhood density” becomes unreliable.
Parameter sensitivity Most density-based algorithms (including LOF, DBSCAN, and others) require one or more parameters (like the neighborhood size, distance thresholds, or the minimum number of points to define a dense region). The accuracy of these methods can vary greatly depending on the chosen parameters. If these parameters are not tuned carefully, the model can either miss outliers or flag too many points as anomalies.
Difficulties with heterogeneous clusters Many real-world datasets exhibit clusters with varying densities. Traditional density-based methods can struggle when one portion of the dataset has higher natural density than another portion. Points in a sparser but “legitimate” cluster could be misclassified as anomalies. Similarly, anomalies that lie within or close to a high-density cluster might go undetected.
Computational cost Most density-based anomaly detection algorithms, like LOF, typically involve pairwise distance computations among data points, which is computationally expensive for large datasets. For each data point, the algorithm may need to determine the k nearest neighbors, and as the dataset grows in size, this process can become a bottleneck.
Limited interpretability These methods identify anomalies by comparing local densities, but explaining precisely why a point is deemed an anomaly (beyond stating that “it resides in a less dense neighborhood”) can sometimes be less intuitive for stakeholders. The conceptual clarity of “low density = anomaly” is straightforward, yet the specific threshold or local measure used can still be confusing to domain experts.
Core Mathematical Formula for LOF
Below is a commonly referenced formula for computing the Local Outlier Factor for a point p in the dataset:
Here:
N_k(p) in plain text means “the set of k nearest neighbors of p”.
lrd(x) means “local reachability density of x”.
|N_k(p)| is the number of neighbors in N_k(p).
The local reachability density of a point p, lrd(p), is the reciprocal of the average “reachability distance” of p to its k nearest neighbors. The “reachability distance” typically involves the concept of k-distance and is designed to measure how easy it is to travel from p to each neighbor.
Follow-up Questions
How do you tune parameters for density-based anomaly detection methods?
Selecting parameters like k (number of neighbors), distance thresholds, or minimum sample sizes can critically affect performance. In practice:
Cross-validation or hold-out sets can be used to systematically try different parameter values and evaluate performance metrics (precision, recall, F1 score).
Domain knowledge about the typical density of “normal” clusters can help guide the choice of parameters. For instance, if you know that normal clusters typically contain at least 50 data points, you might pick minPts around that value for DBSCAN-based algorithms.
Automated hyperparameter optimization methods, such as grid search or Bayesian optimization, can also be employed to find suitable parameter ranges.
What happens if the dataset has multiple clusters with different densities?
When multiple clusters have varying densities, a single global parameter (such as a universal epsilon radius in DBSCAN) often fails to capture these differences. Points in a valid cluster of relatively low density might be deemed outliers, or anomalies within a very dense cluster might remain undetected. One approach is to use hierarchical or adaptive density-based methods that allow varying local thresholds. Alternatively, you can try multi-scale techniques that detect anomalies at different density scales.
How do density-based methods fare in extremely high-dimensional data?
In high-dimensional domains, distance metrics can become less meaningful because the distances between points can concentrate in a small range, making it difficult to distinguish dense from sparse regions. This is a common issue in many clustering and anomaly detection algorithms. To mitigate this:
Dimensionality reduction techniques (PCA, t-SNE, UMAP) can be applied before density-based anomaly detection.
Feature selection or domain-specific transformations can help to reduce the dimensionality while preserving the structure relevant for anomaly detection.
If outliers are also forming their own cluster, can density-based methods handle that?
If a small group of truly anomalous points is sufficiently dense with respect to each other, density-based methods might incorrectly consider them as a normal “micro-cluster.” This error happens because the algorithm sees enough density to treat these points as part of a valid cluster. To address this:
You can set an appropriate minimum cluster size (minPts) so that the outlier cluster is not recognized as a genuine cluster.
You can look for additional indicators of anomalies, such as domain knowledge or other statistical tests, to confirm whether a small cluster is indeed legitimate or anomalous.
A hybrid approach combining density-based methods with distance-based or model-based anomaly detection can offer more robust results.
What are some efficient ways to implement density-based anomaly detection?
Implementing these algorithms in Python can be done via popular libraries such as scikit-learn (which has DBSCAN, OPTICS, etc.) or PyOD (which has LOF, kNN-based anomaly detection, and many others). A typical code snippet for LOF in scikit-learn looks like:
from sklearn.neighbors import LocalOutlierFactor
# X is your input data as a 2D NumPy array or similar
lof_detector = LocalOutlierFactor(n_neighbors=20, contamination=0.1)
y_pred = lof_detector.fit_predict(X)
# Points labeled as -1 by LOF are considered outliers
outliers = X[y_pred == -1]
n_neighbors indicates how many neighbors to use for the density estimation.
contamination can be set if you have an estimate of what fraction of the data is anomalous.
In practice, always verify parameter choices through experimentation and domain knowledge.
Below are additional follow-up questions
Can density-based anomaly detection be adapted for streaming data scenarios?
In real-time applications, data arrives continuously, which means it is impractical to store the entire dataset in memory for offline algorithms like classic LOF. For these scenarios, online or incremental variants of density-based methods have been proposed. They maintain summaries (such as data sketches or micro-clusters) that approximate the local density in a dynamic fashion. However, one significant challenge is the algorithm’s need to update neighborhood structures on the fly. This process can be computationally intensive if the data stream is large or arrives at high velocity.
A practical compromise is to use windowing, where you keep a sliding window of the most recent data points. You apply a density-based method to each window, discarding older data. This approach helps deal with concept drift, where the definition of “normal” can shift over time. Still, if the window is too small, you may lose context; if it is too large, the model updates too slowly. Balancing these window lengths and update intervals is a common pitfall. Another subtlety is maintaining an updated distance structure or nearest-neighbor graph, which can get expensive if not done cleverly, especially as points expire from the window and new points enter.
How do distance metrics affect density-based anomaly detection?
The choice of distance metric underpins how local density is computed. By default, Euclidean distance is common, but it may not reflect the true similarity of data in all domains. For text or embedding-based data, cosine similarity might be more meaningful, whereas in certain multivariate datasets with correlated features, the Mahalanobis distance (which considers covariance) can capture more relevant structure.
One pitfall is using a distance measure that is mismatched to the data representation. For example, applying Euclidean distance in a dataset that is essentially high-dimensional text embeddings might fail to highlight semantically close points. Another subtlety arises when you have mixed data types, like continuous features and categorical variables. A single distance metric might need a careful design (e.g., Hamming distance components for categorical attributes plus numerical distance components for continuous attributes). If the chosen distance metric fails to capture true neighborhood relationships, density-based detection could label legitimate points as outliers or vice versa.
What if the data is non-stationary and exhibits concept drift?
In many practical settings, “normal” behavior changes over time. Examples include network traffic data (where new types of normal traffic might emerge) or financial data (where market conditions evolve). A model trained on historical data may become outdated and start misclassifying new but legitimate patterns as anomalies, or might fail to detect genuinely new anomalies.
One approach is to retrain the density-based model periodically on a rolling window of the most recent data. Another strategy is an incremental learning method that gradually updates local densities as new points arrive. You can also monitor model performance in real time using metrics such as false alarm rate, and trigger a partial or complete model update when performance deteriorates significantly. A subtle pitfall occurs if concept drift is abrupt: the model might get overwhelmed and mislabel many normal points as outliers before it can adjust.
How do density-based methods handle large-scale datasets?
Classic implementations of density-based anomaly detection involve k-nearest neighbor lookups, which are typically O(n^2) in complexity for naive approaches. For very large datasets, this becomes infeasible. To scale up, practitioners often rely on approximate nearest neighbor (ANN) structures such as KD-trees, Ball Trees, or specialized libraries like FAISS or Annoy. These data structures speed up neighbor searches but introduce approximation errors, which can slightly alter the local density estimates.
Another strategy is to sample the dataset, train the density-based model on the sampled subset, and then evaluate outlier scores for the rest. This approach can reduce computational overhead but risks missing local structures in unsampled data. Balancing the trade-off between computational efficiency and accuracy is a common pitfall, as an overly coarse approximation can degrade performance.
How can we integrate domain knowledge into a density-based anomaly detection approach?
While density-based methods are largely unsupervised, domain experts often have partial information about what is (or isn’t) an anomaly. This knowledge could be constraints (e.g., certain ranges of sensor values that are always valid) or known anomalies (labeled examples). One integration strategy is semi-supervised density estimation. You can “anchor” density estimates by forcing certain points to be treated as definitive normal or outlier seeds, guiding the local density calculations. Alternatively, you can apply a post-processing step, where you filter the algorithm’s outlier predictions based on domain-specific rules.
A subtle pitfall is relying too heavily on domain knowledge that may be outdated or incomplete. Over-constraining the algorithm can prevent detection of new anomaly types. Striking the right balance between a purely data-driven approach and domain-informed rules remains a common challenge.
What challenges arise when noise is widespread across the data?
If the dataset includes substantial random noise in otherwise normal points, density-based methods may misclassify these noisy points as outliers. Noise inflates local distances, reducing the density around normal points that suffer from high variance in their feature values. The parameter tuning becomes especially sensitive in this scenario. For example, if k is set too small, noise can drastically affect local density measures. If k is set too large, anomalies might be “averaged out” by many normal neighbors.
In some cases, advanced denoising techniques or robust data preprocessing can mitigate the issue. Tools like autoencoders for denoising or robust scaling methods can help reduce the effect of outliers on the global scale of features. However, these preprocessing steps add complexity and might inadvertently remove or distort actual anomalies.
How do we handle overlapping clusters in density-based detection?
Real-world data often contains overlapping clusters, where boundaries between different “normal” groups are not distinct. A point near the intersection could be in a locally dense region relative to one cluster but still considered part of another. Traditional density-based methods may struggle to accurately label boundary points, especially if the clusters have different densities. One approach is to use specialized algorithms like HDBSCAN or OPTICS that form a hierarchical view of clusters and can handle variable density. However, even these advanced algorithms may incorrectly label boundary points under extreme overlap.
A deeper issue appears when overlapping clusters differ in dimension or shape (e.g., elongated ellipses vs. compact spheres). If the distance metric fails to capture this structure, points could appear anomalous simply by existing in the “gap” between shape-incompatible clusters. Addressing these scenarios might require domain-specific feature engineering or adaptive metrics that reflect the geometry of each cluster.
Is there a way to combine density-based methods with other anomaly detection approaches?
Ensembling is a popular strategy for anomaly detection. By combining density-based methods (like LOF) with distance-based, classification-based, or isolation-based techniques, you can reduce the risk of missing certain anomaly patterns. One way is to stack the outlier scores from multiple detectors into a meta-learner, which then aggregates these scores into a final outlier label. You can also average or take the maximum of the outlier scores directly.
A subtle issue here is how to calibrate different algorithms so that their outputs are comparable. Some methods output binary labels, others produce continuous scores on different scales. Ensuring consistent score distributions usually involves normalization or robust scaling. Additionally, combining too many methods without meaningful diversity can lead to overly complex ensembles that are more difficult to interpret and maintain.