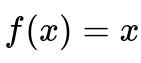ML Interview Q Series: What are the key distinctions between a linear activation function and a non-linear activation function in a neural network?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Linear activation functions compute an output that is directly proportional to the input. In other words, they do not transform the input in any non-trivial way. A typical form of a linear activation function can be expressed in plain text as f(x) = a*x + b, where a and b are constants. The simplest version, often used as an example, is f(x) = x.
Below is the core formula for a basic linear activation function:
Here, x is the input, and the output is exactly the same as the input without any curvature or non-linear transformation.
Non-linear activation functions, on the other hand, create a non-linear relationship between input and output, which introduces the necessary flexibility for neural networks to learn complex, non-trivial mappings. Common examples of non-linear activations are sigmoid, tanh, and ReLU. One highly popular non-linear function is ReLU (Rectified Linear Unit). When you apply a ReLU, the output is 0 for all negative inputs, and for positive inputs it passes the value as is. In plain text, ReLU is f(x) = max(0, x).
Below is the core formula for the ReLU activation function:
Here, x is the input, max(0, x) means if x is less than 0, the output is 0; otherwise, the output is x itself.
Why Linear Functions Alone Are Insufficient
Neural networks that rely entirely on linear activation functions can only represent linear transformations of their inputs, effectively collapsing multiple layers into a single linear transformation. No matter how many layers a purely linear network has, the final outcome remains a linear function of the original input. This severely limits the representational power. Non-linearities allow the composition of multiple layers to represent vastly more complex decision boundaries, patterns, and functions, which is the essence of deep learning.
Impact on Backpropagation
Neural networks learn by adjusting weights based on error signals propagated back through the network. This process depends on the derivative of the activation function. A linear function has a constant derivative (for example, the derivative of f(x) = x is 1). While this doesn't vanish, it also does not allow multi-layer architectures to form complex boundaries. Non-linear functions can have derivatives that vary with input, enabling the network to make sophisticated updates to weights in deeper layers.
Real-World Examples
Deep Convolutional Networks use ReLU or variants like Leaky ReLU and ELU to capture non-linearities in images.
Recurrent Networks often use tanh and sigmoid to control gating mechanisms (e.g., in LSTM cells) to model sequences with complex temporal relationships.
Practical Considerations
Non-linear activations can cause gradient saturation (especially with sigmoid or tanh for very large or very small inputs).
Some non-linear functions, like ReLU, can cause “dead neurons” if the output is always zero due to negative inputs.
Proper weight initialization and careful learning rate selection are critical for effectively training deep neural networks with non-linearities.
Code Example in Python
import torch
import torch.nn as nn
# Linear activation example (just identity)
class LinearAct(nn.Module):
def forward(self, x):
return x # no change to the input
# Non-linear activation example (ReLU)
class ReLUActivation(nn.Module):
def forward(self, x):
return torch.relu(x)
# Example usage:
input_data = torch.tensor([-2.0, -1.0, 0.0, 1.0, 2.0])
linear_layer = LinearAct()
relu_layer = ReLUActivation()
print("Linear Activation:", linear_layer(input_data))
print("ReLU Activation:", relu_layer(input_data))
Follow-Up Questions
Could a neural network with a linear activation function in all layers ever represent a non-linear function?
No. When you stack linear functions, the result is still a linear function. Consequently, multiple layers of purely linear transformations collapse into a single equivalent linear transformation. This removes the main advantage of deep neural networks, which is the ability to learn hierarchical, non-linear representations of data.
Why do non-linear activation functions help with the universal approximation capability of neural networks?
Non-linear activations allow the network to approximate a broad class of functions. The Universal Approximation Theorem states that a feed-forward neural network with even a single hidden layer, equipped with non-linear activation functions, can approximate any continuous function on a compact domain under certain conditions. Without non-linearity, the network is restricted to linear mappings and thus cannot approximate complex functions.
Why might ReLU be preferred over sigmoid in many deep networks?
ReLU, f(x) = max(0, x), does not saturate in the positive region, which helps mitigate vanishing gradients. Sigmoid, being bounded between 0 and 1, tends to saturate for large magnitude inputs, making gradients very small and slowing down learning. ReLU also has a simpler form, speeding up computation.
How does the choice of activation function affect optimization?
An activation function with gradients that frequently vanish or explode can slow or stall training. Properly chosen non-linearities (like ReLU, ELU, or variants) tend to maintain healthier gradients. Also, some activation functions are more sensitive to weight initialization, so the overall network design, initialization scheme, and activation choice are tightly coupled in practice.
Why do some activation functions (like ReLU) lead to dead neurons, and how can we mitigate that?
ReLU can output zero if the input is negative or zero, and once weights adjust to consistently produce negative inputs for a neuron, that neuron can remain at zero output (a dead neuron). Techniques like using Leaky ReLU, Parametric ReLU, or careful initialization can reduce the chance of having many neurons that never activate.
Are there scenarios where a linear activation might still be useful?
Yes. Sometimes the output layer uses a linear activation (for regression tasks) or for specific transformations (e.g., intermediate linear projections). Also, in simpler architectures or certain classical ML models (like linear/logistic regression), the function might be linear or use a logistic function in the final layer. But within deep hidden layers, purely linear activations are generally avoided because they remove the benefits of deeper architectures.
Below are additional follow-up questions
How do skip (residual) connections interact with activation function choices?
Skip connections or residual connections allow information to bypass one or more layers. This design can help mitigate the vanishing gradient problem by letting gradients flow more directly backward. However, the way skip connections intersect with activation functions can be subtle.
When you introduce a residual connection, you effectively add the original input x back to a transformed version of x, typically after an activation function. If the network uses a ReLU or similar activation, the non-linear portion can be added to the bypassed input. This can preserve features from earlier layers while still learning non-linear transformations. In practice:
Residual connections can stabilize training. If the activation function saturates, the skip path still carries forward usable information.
Certain aggressive or experimental activation functions might explode the residual signal. Careful initialization and smaller learning rates can help avoid that.
In real-world deployments, networks like ResNet show significant performance improvements when combining ReLU with skip connections. Researchers also experiment with other non-linearities (e.g., Leaky ReLU, ELU) to see if they further improve stability or accuracy in the residual framework.
What are some considerations for advanced activations like SELU or Swish, and do they outperform ReLU?
SELU (Scaled Exponential Linear Unit) and Swish have gained popularity for certain tasks. They introduce “self-normalizing” or smoothly saturating behaviors that might provide better gradient flow in deeper networks compared to ReLU. However, their benefits can be context-dependent:
SELU requires a specific architecture layout known as Self-Normalizing Neural Networks (SNNs) and can lose its advantage if combined with batch normalization incorrectly. It also assumes a specific data distribution for best results.
Swish is a smooth function that blends linear and sigmoid aspects (f(x) = x * sigmoid(x)). It may improve results slightly in some cases but can be more computationally expensive than ReLU.
Neither SELU nor Swish unequivocally outperforms ReLU across all tasks. They can help in certain deep or complex architectures but may not yield dramatic improvements in every scenario.
Pitfalls include:
If the data distribution violates SELU’s assumptions (e.g., certain initialization or non-symmetric data), performance gains can vanish.
Swish’s derivative can be more complex, raising computational costs or challenges in certain hardware accelerators.
Can non-linear activation functions ever hinder training if they are applied incorrectly?
Yes. Although non-linearities are crucial, they can impede training in various ways:
Non-monotonic or oscillatory functions could cause gradients to behave erratically. This can manifest as large fluctuations in the loss function, making convergence difficult.
Improper initialization with certain activations can lead to immediate saturation. For example, if weights are too large, even a ReLU layer can produce mostly zero outputs on the first forward pass, impeding learning.
In recurrent networks, steep saturations from activations like tanh or sigmoid can lock hidden states, exacerbating vanishing or exploding gradients.
Careful weight initialization, batch normalization (or other normalization techniques), and thoughtful choice of activation can mitigate these issues. If the network architecture does not accommodate the chosen non-linearity (e.g., extremely deep networks without normalization using sigmoid activations), the model may fail to train effectively.
How do you debug activation function issues in a deep network?
When something goes wrong, you might suspect the activation function if:
The activations are saturating at 0 or near their upper bound (for sigmoid, near 1; for ReLU, a large portion of neurons stuck at 0).
The gradients are all zero or extremely large.
Training accuracy plateaus early with no improvement over many epochs.
Steps to debug include:
Inspect distributions of activations: Plot histograms after each layer to see if they’re saturating or if many neurons are dead (in the ReLU case).
Monitor gradients per layer: If they vanish or explode around certain layers, consider switching to a different activation or adjusting initialization.
Use gradient checking or layer-by-layer learning rates to isolate where the problem occurs.
Try simplifying the network architecture (fewer layers, smaller widths) to see if the activation is inherently unsuited to your setup.
Can an activation function cause exploding gradients, similar to how it can cause vanishing gradients?
Absolutely. While vanishing gradients are often the more common complaint—especially with sigmoid or tanh—activation functions can contribute to exploding gradients if:
The derivative in certain ranges becomes very large. A function that sharply increases for moderate input values can amplify small errors into massive updates.
When stacked in multiple layers, even moderate expansions can multiply across layers, eventually exploding the gradient.
While ReLU itself isn’t known for exploding gradients due to its slope being 1 for positive inputs, it can amplify large input values if combined with high weight values in deeper layers. Proper initialization, gradient clipping, and using techniques like batch normalization can help rein in these issues.
Are there differences in how activation functions behave in convolutional layers versus fully connected layers?
The core mathematics of activation functions remains the same in both layer types, but the nature of the inputs is different:
Convolutional layers deal with structured spatial data (e.g., image patches). The local receptive field often leads to a different range of activation inputs compared to fully connected layers. For example, a single convolution filter output might have smaller or more correlated values than a large dense vector in a fully connected layer.
Feature maps from convolutional layers typically undergo batch normalization before activation, stabilizing the input range for the activation function. This approach might differ from some fully connected networks where normalization is applied less frequently.
ReLU in convolutional layers can zero out entire feature maps if the convolution output is negative. This can drastically change the subsequent layers’ representation, so the interplay between convolution kernels and ReLU can be more pronounced than in MLPs.
These differences can make certain non-linearities more or less effective, but the underlying concept of activation remains universal across layer types.
How does activation function choice differ between large-scale production models and smaller experimental models?
When deploying large-scale models:
Speed, memory footprint, and numerical stability become critical. Simple activations like ReLU or variants (Leaky ReLU, ELU) often dominate because they are efficient and well-understood in production pipelines.
More complex functions (e.g., Swish or custom parametric forms) might offer marginal gains but could require extra GPU or TPU instructions. If the marginal gains aren’t large enough, they might not justify the complexity.
Large-scale models often rely on robust engineering practices (e.g., skip connections, layer normalization), reducing the need for fancy activations. The simpler approach is often preferred for reliability and easier troubleshooting.
In smaller prototypes, experimentation is cheaper. One can try different activations like SELU, ReLU6, or Swish without major computational overhead to see if accuracy or convergence speed improves in a controlled environment.
How might weight regularization strategies interact with activation functions?
Weight regularization like L1 or L2 (weight decay) influences the magnitude of learned weights. When combined with certain activation functions:
If the activation saturates (e.g., sigmoid near 1) but weights are large, you may see slow or erratic updates. Regularization keeps weight magnitudes smaller, possibly avoiding early saturation.
Overly large weights in the presence of ReLU can produce extremely high or zero outputs, depending on the sign. L2 regularization might control that blow-up, improving gradient flow consistency.
In convolutional networks, using group or layer normalization plus weight decay can help ensure that no single filter leads to extreme activation outputs that hamper training.
Pitfalls include balancing the regularization coefficient with the activation’s sensitivity. Too much regularization can underfit; too little can cause unstable or exploding signals in deeper networks.
Under what conditions might a piecewise linear function like ReLU fail, and how can we address that?
Piecewise linear functions like ReLU (with a “kink” at 0) fail to capture phenomena that require smoothness or negative domain representation. Specific issues include:
Purely negative input regions produce zero outputs, which can stall learning if the network consistently outputs negative pre-activations.
Many neurons can die off (the “dead ReLU” problem), leading to underutilized capacity.
Sharp transitions might not approximate smooth functions well in certain specialized tasks like wave modeling or some continuous control applications.
To address these:
Use alternative variants like Leaky ReLU or ELU, which allow for a small negative slope and reduce neuron “death.”
Perform careful weight initialization so that the distribution of inputs falls into the positive region often enough.
Consider advanced activations like Swish or GELU if smoothness is critical.
What role do activation functions play in attention mechanisms or transformer architectures?
Transformers rely heavily on linear transformations (for queries, keys, and values) and softmax operations for computing attention weights. Inside feed-forward blocks in a transformer, a non-linear activation (commonly ReLU or GELU) is still essential. This ensures:
The model captures non-linear dependencies between the attended features, adding representational power beyond simple linear transformations.
GELU has become a standard choice in many modern transformer variants. Because it’s smoother than ReLU, it can help the model learn nuanced relationships within token embeddings.
A pitfall in certain transformer implementations is ignoring activation function scaling or ignoring how layer normalization interacts with it. If the activation drastically modifies the magnitude of the embeddings, the subsequent attention or layer normalization step could lead to poor gradient flow or attention collapse. Careful hyperparameter tuning around the activation’s shape, dropout, and learning rate often addresses these concerns.