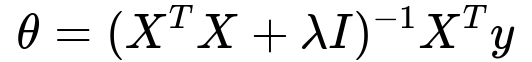ML Interview Q Series: What are the key benefits of using Gradient Descent instead of the standard Ordinary Least Squares method for linear regression?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

One way to solve for linear regression parameters is using the closed-form solution based on Ordinary Least Squares. The closed-form solution can be expressed as

Here, X is the design matrix of shape m x n (m is the number of samples, n is the number of features), y is the vector of targets of length m, and (X^T X) is an n x n matrix. The expression (X^T X)^{-1} represents the matrix inverse of (X^T X).

In contrast, gradient descent relies on iterative updates of parameters to minimize the cost function. If J(theta) is the mean squared error cost function in linear regression, the typical gradient descent update rule is:

where alpha is the learning rate and ∇theta J(theta) is the gradient of the cost function with respect to the parameters theta.

Advantages of Gradient Descent over Ordinary Least Squares:

Handling very large feature sets. When the number of features becomes extremely large, computing (X^T X) and its inverse can be impractical in terms of time and memory. Gradient descent can process data in batches or even in stochastic modes, making it more feasible to handle large-scale problems.

Flexibility with incremental training. Gradient descent can be used in an online or mini-batch fashion, allowing updates to be made to the model parameters as new data arrives. This is particularly beneficial in streaming applications or scenarios where data does not fit into memory all at once.

Reduced risk from matrix invertibility issues. In certain cases, (X^T X) can be nearly singular or ill-conditioned. Ordinary Least Squares would require inverting this matrix, which might produce unstable results or fail outright. With gradient descent, we never invert (X^T X), so we avoid these numerical stability issues.

Potential for extensions beyond linear regression. Gradient descent is a fundamental optimization tool that can be directly applied to models where no simple closed-form solution exists (such as logistic regression, neural networks, and other complex models). Hence, the same procedure used in linear regression can be easily generalized to other tasks.

Lower upfront computational cost for large datasets. While each individual gradient descent iteration can be relatively cheap, the closed-form OLS approach can sometimes involve expensive matrix operations of order O(n^3) for the inversion step (where n is the number of features). By comparison, each gradient descent iteration is typically cheaper, although you may need several iterations to converge.

Suitability for parallel/distributed computing. Gradient-based methods can be parallelized or distributed more readily (for example, using distributed frameworks with mini-batch gradient descent). This is especially useful when training data is extremely large and scattered across multiple machines.

Implementation Example

Below is a simple Python code snippet demonstrating the use of batch gradient descent for linear regression. This sample is only to illustrate the iterative approach.

import numpy as np

def gradient_descent_linear_regression(X, y, alpha=0.01, epochs=1000):
    # X: m x n design matrix
    # y: m-dimensional target vector
    # alpha: learning rate
    # epochs: number of iterations

    m, n = X.shape
    theta = np.zeros(n)

    for _ in range(epochs):
        # Predictions
        y_pred = X.dot(theta)

        # Compute gradient of MSE cost
        gradient = (1.0 / m) * X.T.dot(y_pred - y)

        # Update step
        theta = theta - alpha * gradient

    return theta

# Example usage
# Suppose we have a dataset with m=100, n=3
# X_ is the design matrix (100 x 3), y_ is the target vector (length 100)
# alpha_ = 0.1, epochs_ = 500
# final_theta = gradient_descent_linear_regression(X_, y_, alpha=alpha_, epochs=epochs_)
# print("Learned parameters:", final_theta)

This iterative procedure avoids calculating an inverse directly. The bigger your dataset or the more features you have, the more appealing such an approach often becomes.

How to Choose the Learning Rate

Choosing alpha is crucial. If alpha is too large, you can overshoot the minimum and fail to converge. If alpha is too small, the training will converge extremely slowly. Techniques like line search, adaptive learning rates (e.g., AdaGrad, RMSProp, Adam in deep learning contexts), or simply systematically trying different alpha values are common ways to find a suitable step size.

Follow-up Questions

What scenarios favor the closed-form solution over Gradient Descent?

When the feature dimension is not excessively large and computing (X^T X) and its inverse (or using more stable matrix factorization techniques like QR or SVD) is feasible, the closed-form solution can be extremely fast and numerically stable. Small to medium-scale problems can often benefit from a direct solution because it requires no tuning of the learning rate and converges in a single shot.

Could Gradient Descent get stuck in local minima for linear regression?

For linear regression with the mean squared error cost function, the surface is convex with a single global minimum. Hence, gradient descent will not get stuck in a local minimum. It is still possible to have numerical issues or diverge if alpha is poorly chosen, but it does not suffer from local minima problems for ordinary least squares linear regression.

Why is matrix invertibility a concern in OLS?

In some datasets, especially if features are highly correlated or there are more features than data points, (X^T X) can become nearly singular or ill-conditioned. This leads to potential numerical instability when inverting the matrix. Gradient descent simply iterates over the data and updates parameters incrementally, so it circumvents the direct inverse operation and tends to be more stable in such situations.

How can we adapt Gradient Descent for streaming or large-scale data?

Mini-batch or online gradient descent processes portions of the data at a time instead of the entire dataset. This allows model updates to be done in smaller steps, potentially making it easier to handle massive datasets that do not fit in memory. Stream processing frameworks can be integrated to update the parameters on-the-fly as new data arrives.

How does one ensure convergence in Gradient Descent?

Ensuring convergence often involves: Adjusting the learning rate. Using schedules that decay the learning rate over time or using adaptive methods (like Adam) can stabilize training. Monitoring the change in the cost function. Once the cost stops decreasing meaningfully, training can be halted. Checking gradients for vanishing or exploding values and implementing measures (like gradient clipping) in more complex models.

These techniques help keep the gradient descent updates stable and steadily moving toward the global optimum in linear regression.

Below are additional follow-up questions

How do you determine an appropriate number of iterations (epochs) for gradient descent in linear regression?

One approach is to monitor the value of the loss function—often the mean squared error—and observe when improvements become negligible. If you see that the cost function plateaus, continuing to train may not lead to further meaningful improvements. A common strategy is to set a maximum number of iterations (epochs) based on computational constraints and then include an early stopping criterion that checks whether the change in cost is below some small threshold for a specified number of consecutive steps.

A more systematic approach might involve performing multiple runs with different numbers of epochs and choosing the one that strikes the best balance between computational cost and model accuracy. In practice, you would track the training error and potentially a validation error if you are using a validation set. When those errors stop decreasing consistently, that often signals a good cutoff point.

Potential pitfalls can arise if the chosen iteration limit is too low; you might terminate before properly converging. Conversely, a very large iteration limit wastes time and can sometimes cause overfitting if the data is noisy. Though linear regression with mean squared error is less prone to overfitting strictly through more iterations, it’s still a practical consideration in real-world applications where data might not perfectly fit a linear model and where the training objective could include additional regularization terms.

What is the difference between batch, stochastic, and mini-batch gradient descent in linear regression?

Batch gradient descent (BGD) uses the entire dataset to compute the gradient at each iteration. This ensures the gradient direction is very accurate with respect to the true cost function but can be computationally expensive when the dataset is large.

Stochastic gradient descent (SGD) updates parameters using one training example at a time. This is computationally cheaper per update and introduces randomness, which sometimes helps escape shallow local minima in non-convex problems. In pure linear regression, the cost function is convex, so the randomness mostly affects the trajectory but not the global optimum location (assuming sufficient convergence steps).

Mini-batch gradient descent (MBGD) strikes a balance by using small batches (e.g., 32, 64, or 128 samples) to compute an approximate gradient. It typically converges faster than BGD in wall-clock time and is less noisy than pure SGD. In practice, mini-batch GD is often the default choice, especially for larger datasets or deep learning models, because it is efficient and can leverage parallel hardware (like GPUs).

A subtle pitfall is choosing a mini-batch size that is too large or too small. Too large a batch size can sometimes behave like BGD and slow down iteration progress. Too small a batch can introduce excessive variance in gradient estimates. The ideal balance depends on the hardware and data characteristics.

How do outliers affect linear regression, and are there any differences in the way outliers impact gradient descent versus OLS?

Outliers can heavily skew the solution for linear regression when using the standard mean squared error cost. In OLS closed-form calculations, a single (X^T X) outlier can have a disproportionately large influence on the solution, causing the inversion or factorization to be driven by these extreme points.

When using gradient descent with a standard MSE loss, outliers similarly affect the gradient since the error term for that outlier is large. The model’s updates will place significant emphasis on reducing the error for these points, potentially at the expense of the rest of the dataset. However, in practice, gradient descent can sometimes be slightly more robust when implemented with certain heuristics (like lower learning rates or robust loss functions) because each iteration only moves the parameters incrementally.

A pitfall emerges if the outliers are extreme and the learning rate is too high—gradient descent might produce very large updates that destabilize training. One way to mitigate this is using a robust cost function (e.g., Huber loss) that reduces the impact of outliers. Another approach is preprocessing the data to detect and handle outliers before training.

Is feature scaling important for gradient descent in linear regression, and why?

Feature scaling involves standardizing or normalizing input variables so that each feature has a comparable range (e.g., zero mean and unit variance). This is crucial for gradient descent because, in unscaled data, one feature with a very large numeric range can dominate the gradient calculation, causing inefficient or oscillatory convergence.

By scaling features, you ensure that the contour lines of the cost function are more “spherical.” This simplifies the path gradient descent travels to reach the minimum, often speeding up convergence substantially. Without feature scaling, you might need a very small learning rate to ensure stability.

A potential pitfall is forgetting to apply the same scaling transformation to new data or the test set. This discrepancy will degrade model performance. It’s also important to store the scaling parameters (mean, standard deviation, or min-max values) from your training set and apply them consistently when deploying or evaluating your model.

How can we incorporate regularization in gradient descent, and how does that compare to the closed-form solution for regularized linear regression?

Regularized versions of linear regression—like ridge regression—add a penalty term lambda * sum(theta_j^2) to the cost function (excluding the intercept term). In gradient descent, you simply add the gradient of that penalty term to the gradient update:

theta_j <- theta_j - alpha * (d/d(theta_j)[MSE] + lambda * 2 * theta_j / m)

(assuming the intercept is not regularized, you skip the j=0 parameter). This approach is straightforward and can be adapted to other forms of regularization (e.g., L1-norm for Lasso).

In the closed-form solution for ridge regression, we get:

Here, lambda is the regularization parameter, and I is the identity matrix of dimension n x n. Although the closed-form is typically stable if lambda is not zero, for very large dimensional data, inverting (X^T X + \lambda I) might still be expensive. Gradient descent provides a simpler and more scalable approach, especially for big data scenarios or when incremental training is desired.

One major pitfall is the selection of lambda. Too large a lambda can overly shrink parameters, causing underfitting; too small a lambda can fail to address overfitting. Hence, hyperparameter tuning is critical.

If the cost function is not convex, can gradient descent still converge to the global optimum?

For linear regression with a mean squared error cost, the function is convex, so there is only one global minimum, ensuring gradient descent can converge to that minimum (barring numerical issues). However, when you extend linear regression with non-linear transformations (e.g., polynomial regression) or move to deep neural networks, the loss surface can contain multiple local minima or saddle points.

In such non-convex settings, gradient descent might converge to a local minimum or get stuck in a plateau. Various strategies (like momentum-based optimizers, adaptive learning rates, or restarts) can help the model escape shallow local minima or saddle points, although a guarantee of finding the global optimum typically does not exist for complex non-convex problems.

A subtle pitfall is incorrectly assuming that all gradient descent problems are convex. Confusing a straightforward linear regression scenario with a more general non-convex one might lead to misunderstandings about convergence guarantees.

What are some strategies to detect or mitigate divergence in gradient descent?

1. Monitoring the cost function: If you see the cost function growing exponentially or failing to decrease consistently, it often indicates the learning rate is too high. Reducing the learning rate can stabilize training.

2. Gradient norm checks: By checking the magnitude of the gradient, you can detect exploding gradients. If the gradient norm is extremely large, gradient clipping or lowering the learning rate may help.

3. Adaptive learning rates: Methods like RMSProp or Adam automatically adjust the learning rate during training based on recent gradient statistics. This often prevents divergence from a poorly chosen fixed learning rate.

4. Learning rate schedules: Using a schedule that decays the learning rate over time is another way to control divergence and refine convergence once you are near an optimum.

A hidden pitfall is ignoring slow divergence. In some cases, cost might fluctuate within a small range for many iterations and then explode, so continuously monitoring throughout training is important.

How does the choice of initialization for theta matter in linear regression compared to more complex models?

In linear regression with mean squared error, the cost function is convex and the global optimum is unique (assuming a full-rank design matrix). You can initialize theta to zeros or small random values, and gradient descent should still converge to the same optimum. The main effect might be the speed of convergence, but it is typically minor compared to choosing a suitable learning rate and doing feature scaling.

In more complex, non-convex models (e.g., neural networks), initialization is crucial because different initial values can lead to different local minima or training behaviors. Consequently, advanced initialization methods (like Xavier or He initialization) become important in deep learning, but for simple linear regression, basic initializations are sufficient.

Can the learning rate be adapted during training, and how does it help in linear regression?

Yes. You can adapt the learning rate in several ways:

• Learning rate decay: Decrease alpha over epochs, allowing large initial updates and finer adjustments later.

• Adaptive optimizers: Adam, Adagrad, and RMSProp adjust the step size per parameter automatically based on gradient history.

In linear regression, adapting alpha might not always be strictly necessary because the problem is convex. However, a slightly higher initial alpha can speed convergence, and a smaller alpha later helps refine the solution without large oscillations. Overly large alpha values risk divergence, while overly small alpha values slow down convergence. Dynamically tuning alpha can address both concerns in a single framework.

What is the computational complexity of gradient descent for large-scale linear regression, and how does that compare to the closed-form OLS solution?

• Closed-form OLS: The primary cost arises from computing (X^T X) (cost roughly O(mn^2)) and then inverting an n x n matrix (cost roughly O(n^3) using standard methods). For very large n, this becomes computationally expensive.

• Gradient Descent: Each full batch iteration typically requires O(mn) operations to compute predictions (X dot theta) and the gradient (X^T dot (y_pred - y)). Suppose you run a total of T iterations, then the overall cost is approximately O(Tmn). The value of T needed to converge can vary, but for large n, gradient descent is often more efficient, especially when T << n or when combined with mini-batch strategies that process subsets of data.

A significant real-world pitfall is to assume that gradient descent always converges very quickly. With poor hyperparameter choices (such as learning rate or mini-batch size), T might need to be extremely large. Another issue is memory constraints: computing X^T X directly requires storing an n x n matrix, which may be infeasible if n is extremely large, whereas gradient descent methods can process data in chunks, alleviating memory issues.