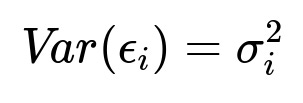ML Interview Q Series: What differentiates homoskedastic from heteroskedastic residuals, how to detect and address measurement error-induced heteroskedasticity?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Homoskedasticity refers to a situation in which the variance of the error terms in a regression model remains constant across all levels of the independent variables. When this assumption holds, the variance of the residuals does not depend on the magnitude of the predictors. In contrast, heteroskedasticity is when the variance of these error terms changes as a function of the predictors or their predicted values.

A fundamental expression for homoskedasticity is shown by stating that the variance of the residual terms is a constant sigma^2, while heteroskedasticity indicates the variance is no longer a fixed value and might vary from one data point to another.

This represents the homoskedastic scenario, where sigma^2 is constant for all i.

In this heteroskedastic scenario, the variance sigma_i^2 depends on i (e.g., changes with a particular feature level).

The presence of heteroskedastic errors complicates various analytical procedures, including hypothesis tests and confidence interval estimations, because the usual ordinary least squares assumptions no longer hold. For instance, the default estimates of standard errors in ordinary least squares would be unreliable, potentially causing misleading test statistics.

Detecting heteroskedasticity can be done in multiple ways. A common method is plotting the residuals against the predicted values and visually checking if the spread of the residuals increases or decreases. If the scatter of residuals widens or narrows systematically, it is indicative of heteroskedasticity. Statistical tests like the Breusch-Pagan test or the White test offer more formal ways to verify if there is a significant relationship between predicted values (or certain functions of the features) and the squared residuals.

When the root cause of heteroskedasticity is measurement error, particularly where the variability in measurement scales increases for larger values of the dependent variable or the predictors, the direct outcome is that observations at higher levels might exhibit bigger fluctuations in errors than observations at lower levels. If left unaddressed, this can lead to biased or inefficient parameter estimates and flawed inference.

One approach to handle measurement-error-induced heteroskedasticity is transforming the variable whose measurement scales change across the observed range. For example, if larger values produce proportionally larger errors, a log transform can help reduce the multiplicative effect of the measurement scale. Another strategy is weighted least squares, where each data point is assigned a weight that is inversely related to the variance of its error term. This ensures that observations with lower error variance exert a proportionally larger influence on the parameter estimates.

If it is known in advance that the measurement error follows a particular relationship (for instance, error variance might be proportional to the square of the magnitude of a measurement), carefully chosen variance-stabilizing transformations or a well-matched weighting scheme can correct for the heteroskedasticity in the model. In more advanced methods, robust standard errors or generalized least squares techniques can also be adopted, where the structure of the residual covariance matrix is explicitly accounted for, thus directly handling the non-constant variance arising from measurement errors.

How does measurement error typically lead to heteroskedasticity?

Measurement error can be correlated with the scale of the measured quantity. When the magnitude of a measurement grows, the corresponding error might grow as well in absolute or relative terms. This is particularly common in scenarios where measurements are more challenging or less precise at higher values (for instance, scanning higher signal intensities might produce higher noise). This violates the constant variance assumption of ordinary least squares because the spread of errors depends on the actual level of the measurements.

How does one formally test for heteroskedasticity in practice?

Visual inspection of residual-versus-predicted-value plots can be an intuitive first step. Statistical testing can then be done using procedures like the Breusch-Pagan test or the White test. These tests involve regressing the squared residuals on the predictors (or transformations thereof) to see whether there is a significant relationship. If the test reveals significance, it indicates that the variance of residuals is not constant, i.e., we have heteroskedasticity.

Can you provide a code example in Python for detecting heteroskedasticity?

import numpy as np
import statsmodels.api as sm
from statsmodels.stats.diagnostic import het_breuschpagan

# Example data
np.random.seed(42)
X = np.random.rand(100, 1)*10
y = 2*X.squeeze() + np.random.randn(100)*2*(X.squeeze())  # artificially heteroskedastic

# Add intercept
X_ = sm.add_constant(X)

# Fit OLS model
model = sm.OLS(y, X_).fit()

# Breusch-Pagan test
# The first return value is the Lagrange multiplier statistic, the second is its p-value
bp_test = het_breuschpagan(model.resid, model.model.exog)
print("Lagrange multiplier statistic:", bp_test[0])
print("p-value:", bp_test[1])

This code snippet uses the Breusch-Pagan test to formally detect heteroskedasticity. A low p-value indicates strong evidence of non-constant variance in the residuals.

What remedies can be used if the heteroskedasticity is induced by measurement error?

If the measurement errors vary systematically with the level of a variable, the variance-stabilizing transform is often the first line of defense. If the standard deviation of the measurement error is proportional to the magnitude of the variable itself, a log transform can reduce the proportional effect of that error. Weighted least squares is another method, where each point is given a weight that reflects the inverse of the expected variance. In more advanced setups, generalized least squares accounts for a covariance structure in the errors, while robust standard errors can at least correct the standard error estimates for heteroskedasticity.

When measurement error can be reasonably assumed to follow a parametric form (for example, error variance increasing quadratically with the measured values), incorporating domain-specific knowledge into the model can significantly improve estimates. Calibration experiments, external data about measurement device precision, or known properties of the measurement process can all help in designing an appropriate weighting function or transformation.

Why is correcting for measurement-error-induced heteroskedasticity critical?

Unaddressed heteroskedasticity can lead to inefficient parameter estimates. Standard error estimates typically assume homoskedasticity, and under heteroskedastic conditions they become inaccurate, potentially causing incorrect conclusions from hypothesis tests. In the worst case, certain predictions or inferences might be systematically biased if the model structure is not flexible enough to account for the heteroskedastic error term.

Failure to address these issues could result in models that overstate their accuracy and produce confidence intervals that are narrower or broader than they should be, ultimately undermining trust in the model’s predictions, especially when deploying in high-stakes applications.