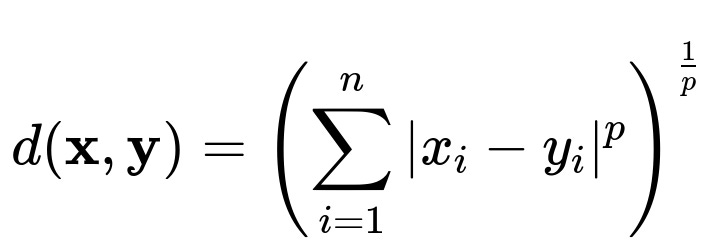📚 Browse the full ML Interview series here.
Comprehensive Explanation
When dealing with purely quantitative (numeric) features, one of the most common ways to measure distance or similarity is to use Minkowski-based distance metrics. Two prominent examples are the Euclidean distance and the Manhattan distance. Each one is a special case of the more general Minkowski distance.
Minkowski Distance
The Minkowski distance of order p between two points x and y, each in an n-dimensional space, can be expressed by the formula shown below.
Here, x and y are both vectors with n components. For each dimension i, you take the absolute difference |x_i - y_i|, raise it to the power p, sum these across all n dimensions, and then take the pth root of that sum. The parameter p controls the nature of the distance metric. Some important special cases are:
p=1: This is the Manhattan distance, which sums the absolute differences across each dimension.
p=2: This is the Euclidean distance, which sums the squared differences, then takes the square root.
Euclidean Distance
This is the most common distance function for real-valued data. It is a specific case of the Minkowski distance where p=2. It measures the geometric distance in n-dimensional space by:
It tends to work well in many scenarios where data points lie in a space where the magnitude of differences matters in a squared sense. It also has geometric interpretations in terms of straight-line distances in Euclidean space.
Manhattan Distance
Another frequently used metric is the Manhattan distance (p=1), which is the sum of the absolute differences across each dimension. It is especially relevant in high-dimensional sparse problems or in scenarios where the notion of distance is more akin to grid-like movement rather than diagonal shortcuts.
Manhattan distance is given by summing the absolute differences |x_i - y_i| for each dimension i. It can be more robust in certain high-dimensional data spaces, as it can emphasize axis-aligned differences rather than diagonal ones.
Practical Implementation Example in Python
import numpy as np
def minkowski_distance(x, y, p=2):
# x and y are numpy arrays of the same shape
return np.sum(np.abs(x - y)**p)**(1/p)
# Example usage
x = np.array([1.0, 2.0, 3.0])
y = np.array([2.0, 4.0, 4.0])
dist_euclidean = minkowski_distance(x, y, p=2) # p=2
dist_manhattan = minkowski_distance(x, y, p=1) # p=1
print("Euclidean Distance:", dist_euclidean)
print("Manhattan Distance:", dist_manhattan)
The above implementation shows how to calculate Minkowski distance in Python. By choosing different p values, one can convert it to Euclidean (p=2) or Manhattan (p=1).
When to Choose Which Distance Metric
Selecting a distance function depends heavily on the nature of your data and the problem context. Euclidean distance is a strong default choice for continuous numerical data when scale and magnitude matter. However, when certain features might not be meaningfully squared or when outliers or high-dimensional effects are a concern, practitioners sometimes switch to Manhattan or other distance measures like Chebyshev (max norm) or more specialized metrics.
Potential Follow-up Questions
What if some of my numerical features are on vastly different scales?
In such cases, consider normalizing or standardizing your features before computing distances. Without standardization, features with large numeric ranges may dominate the distance calculation, leading to biased results. Standard scaling (subtract mean, divide by standard deviation) or min-max scaling (rescale the range to [0, 1]) are common preprocessing steps.
How do I handle missing values when computing these distances?
There are several strategies to handle missing data in distance computations:
Impute missing values using statistical techniques (mean, median, or more advanced methods like kNN imputation).
Compute the distance only over the dimensions where both points have valid data and adjust the formula accordingly.
Use specialized distances that can handle missing values explicitly (though these are less common).
Why might Manhattan distance sometimes be preferred in high-dimensional spaces?
When the number of features (dimensions) is large, Euclidean distance can become less intuitive due to the “curse of dimensionality.” Manhattan distance sometimes can be more stable, as each dimension contributes linearly to the overall distance, and large squared distances along any single dimension have a less disruptive effect. This can give more balanced distance values in certain high-dimensional scenarios.
How does the Minkowski distance generalize to other norms?
By varying the parameter p:
p=1 yields Manhattan distance.
p=2 yields Euclidean distance.
p→∞ yields the Chebyshev distance, which is the maximum absolute difference among any dimension.
Non-integer values of p also exist in theory, though they are less commonly used in mainstream machine learning practice.
These variations all derive from the Minkowski formulation and can be seen as Lp norms.
Could I use correlation-based distances instead of Minkowski distances for quantitative data?
Yes, especially if your aim is to capture how variables co-vary rather than how far they are in absolute scale. Correlation-based distances or similarity measures (e.g., Pearson correlation) can be useful when you care about the shape or trend of the data rather than direct magnitude differences. However, correlation-based measures usually ignore the absolute scale and might not be appropriate if raw magnitude comparisons are important in your problem.
Could the choice of distance metric affect the performance of algorithms like k-NN or clustering?
Absolutely. Clustering and nearest neighbor algorithms fundamentally rely on the notion of distance. If the distance does not appropriately reflect the “closeness” of data points in your problem domain, these algorithms can perform poorly. Always choose a metric aligned with how you conceptually define similarity for your data.
In summary for Quantitative Data
Euclidean distance is typically the go-to distance measure for quantitative data, with Manhattan distance and other Lp norms employed when certain conditions (like robustness to outliers, high-dimensional considerations, or certain geometric properties) are needed. The general framework of Minkowski distance unifies many of these distance functions and helps you systematically select a measure based on problem-specific considerations.
Below are additional follow-up questions
How do outliers or extreme values in the data affect the choice of distance metric?
Outliers can heavily influence distance calculations if you use Euclidean distance because squaring the difference amplifies large deviations. Consequently, points with outlier values may end up dominating distance measures, overshadowing more typical variations in other dimensions. Manhattan distance is slightly less sensitive to extremely large differences in a single feature since it relies on absolute differences rather than squared differences, but it can still be influenced by very large outlier values if the magnitude is high.
A potential pitfall is that if your dataset contains a handful of extreme outliers, these points might erroneously appear “far” from all other data points, sometimes causing methods like k-NN or distance-based clustering to degrade in performance. Common strategies to handle outliers include trimming, Winsorizing (capping the outliers), or applying robust scalers (e.g., using interquartile range). Alternatively, you might choose a more robust distance metric that reduces the impact of extreme values.
What if my features are highly correlated with each other?
When features are strongly correlated, using straightforward Minkowski distances (including Euclidean) might cause redundant dimensions to disproportionately affect the distance. For example, if two features essentially measure the same quantity, a difference in that quantity is effectively counted multiple times. This redundancy can distort how distances reflect the real underlying relationships among data points.
One approach to mitigate this pitfall is to apply dimensionality reduction methods such as Principal Component Analysis (PCA). By transforming correlated features into orthogonal principal components, you reduce redundancy and can then apply standard distance metrics in the lower-dimensional or decorrelated space. Alternatively, you can incorporate a Mahalanobis distance approach (which accounts for feature correlations via covariance matrices) if you suspect that correlated features are vital for measuring the true distances in your data.
How do we handle data that is numeric but follows a cyclical pattern?
Some quantitative features are inherently cyclical, such as time-of-day (hours in a day) or angles in degrees. Directly computing standard Euclidean or Manhattan distances on raw values might incorrectly indicate two times (e.g., 23:59 and 00:00) as being far apart numerically, when in reality they are only a minute apart.
The main pitfall is ignoring the circular nature of such features. A standard approach is to transform cyclical features into a pair of coordinates (e.g., sin and cos transformations for angles or time). By doing this, you map the features onto a circle rather than a straight line. This way, the distance metrics naturally capture the circular proximity. Alternatively, you could design or select distance functions that “wrap around” for cyclical data.
When might you consider a custom distance metric for numeric data?
Sometimes, neither Euclidean nor Manhattan distance adequately captures domain-specific nuances. For example, if you have specialized medical data, you might want to incorporate expert knowledge that certain features (like specific biomarkers) are more important than others or that the difference in one biomarker translates to a particular risk measure. In these cases, you can define custom distance functions that weight certain features differently or apply domain-specific transformations prior to distance calculations.
A major pitfall is employing a generalized distance measure that overlooks critical domain-related distinctions, leading to misguided distance-based reasoning. By crafting a custom metric that aligns well with domain experts’ understanding, you can capture subtle differences that standard metrics may miss.
How do we choose the parameter p in the Minkowski distance in practice?
Choosing p for the Minkowski distance often depends on experimentation and cross-validation. p=2 (Euclidean) is the default in many scenarios, but p=1 (Manhattan) can be preferable for high-dimensional datasets or when data has heavy-tailed distributions. Some practitioners attempt fractional values of p (e.g., 1.5 or 3) to see if that yields better performance for certain tasks, though this is less common.
A practical approach is to treat p as a hyperparameter. You can: • Split your data into training and validation sets (or use cross-validation). • Vary p (for instance, 1, 1.5, 2, 3) in the distance metric used by your learning algorithm (e.g., k-NN). • Evaluate performance metrics (accuracy, F1-score, etc.) on the validation set. Choose the p that yields the best performance.
The main pitfall is defaulting to p=2 without checking whether another choice might be more suitable, especially if you suspect that your data distribution might favor an alternative.
If the dataset is extremely large, how do we compute these distances efficiently?
Calculating pairwise distances across very large datasets can be computationally expensive, as a naive approach may require O(N^2) distance computations (for N data points). Some techniques to handle this challenge include: • Approximate Nearest Neighbor (ANN) search structures like KD-trees or ball trees (although these degrade in high dimensions). • Locality Sensitive Hashing (LSH) methods that allow for sublinear retrieval of near neighbors under certain distances. • Using batch-based or distributed computing frameworks such as Apache Spark or Dask to parallelize distance calculations. • Dimensionality reduction to reduce the cost per distance computation.
A significant pitfall is assuming that your standard distance computations will scale well to millions of data points without considering approximate methods or distributed infrastructure. In practice, engineering solutions that parallelize or approximate distance computations are often critical in large-scale scenarios.
What strategies exist for dealing with partial numeric data or missing measurements in distance calculations?
Partial numeric data arises when some feature values are missing for certain observations. If your distance function cannot handle missing values, you may end up discarding those observations or ignoring dimensions with missing entries, which could lead to biased results. Potential solutions include: • Imputing missing values via statistical methods (mean, median, or regression-based). • Model-based imputation (e.g., kNN imputation itself, in which distances are computed only for the available features). • Using a distance function that dynamically skips or weights missing dimensions (less common but possible in specialized contexts).
The pitfall here is ignoring the mechanism causing the data to be missing. If the data is not missing completely at random, simply imputing without caution might introduce additional biases or artificially shrink distances. Always investigate the data’s missingness patterns and mechanism to avoid inaccurate distance computations.
How can we handle numeric data living on curved manifolds or with non-Euclidean geometry?
Certain data types—like points on Earth’s surface in latitude/longitude format—reside on a sphere (or approximate spheroid), so using straight-line Euclidean distance on latitude and longitude values may be misleading. Instead, one should use geodesic distances (like the great-circle distance) that reflect the curvature of the sphere.
When data lies on more complex manifolds (e.g., manifolds arising from advanced dimensionality reduction), the concept of distance may need to be defined in a manifold-appropriate way (e.g., geodesics on that manifold). The pitfall is applying standard Euclidean distances to curved or manifold data, leading to incorrect nearest-neighbor relationships and misleading cluster shapes. Adapting the distance metric to the geometry avoids such misrepresentations.
Does weighting individual dimensions help, and when is it necessary?
Weighting different dimensions can be critical when certain features have different levels of importance or reliability. A weighted Minkowski distance might look like summing w_i * (|x_i - y_i|^p), where w_i is the weight for the i-th feature. This effectively amplifies or attenuates the contribution of each feature to the overall distance. You might choose weights based on domain knowledge or optimize them as hyperparameters.
The pitfall is leaving all weights at 1 by default, even when domain knowledge strongly indicates certain features should be emphasized or de-emphasized. Another risk arises from improperly tuning the weights, which can inadvertently distort distances. Good practice involves systematically testing or validating weight choices and ensuring they reflect meaningful differences in data features.