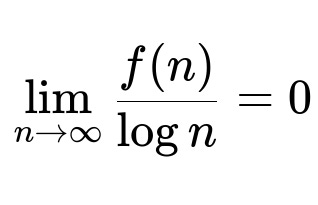ML Interview Q Series: What does it imply when an algorithm’s running time is characterized as o(log n)?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

When we say that a function f(n) is o(log n), we are using the “little-o” notation from asymptotic complexity theory. This means f(n) grows strictly slower than log n as n becomes very large. Formally, for f(n) = o(log n), it indicates that if we take the ratio f(n) / log n and let n grow toward infinity, that ratio approaches 0.

Here f(n) is the time complexity of the operation, and log n is another function in terms of n. The notation “o(log n)” says that f(n) / log n goes to 0 as n goes to infinity. Another way to put it is that f(n) grows more slowly than any constant multiple of log n.

For many engineers, the more commonly used notation is O(log n), meaning f(n) does not exceed some constant multiple of log n for large n. But “little-o” is stricter: it means that no matter how small a constant factor c we choose, eventually f(n) will be smaller than c * log n. In simpler terms, if an operation’s complexity is o(log n), it is bounded by something that expands more slowly than log n, such as constant time, sqrt(log n), or log(log n). Thus, “o(log n)” is a guarantee of growth that is definitely below log n asymptotically.

Related Details

Distinguishing Big-O and Little-o

• If we say f(n) = O(log n), we mean f(n) can grow on the same order as log n. • If we say f(n) = o(log n), we mean f(n) grows more slowly than log n. Specifically, log n is an upper bound that is not tight for f(n).

Practical Example

Imagine a function that reads only a fraction of the data, whose size grows extremely slowly as n increases (for instance, a specialized indexing scheme or a random sampling). Such an approach could, in theory, run in time that is smaller than log n for large n. That would make the function o(log n).

Sample Code Context

def sub_logarithmic_example(n):
    """
    Hypothetical function that performs a constant number of operations,
    effectively O(1), which is also o(log n).
    """
    result = 0
    # Just do a fixed number of operations
    for _ in range(10):
        result += 1
    return result

In this code snippet, the function does the same 10 operations regardless of n. Since the runtime is constant O(1), it is also o(log n) because constant time grows more slowly than log n.

Potential Follow-Up Questions

How does o(log n) compare to O(1)?

When an operation runs in O(1) time, it is also o(log n). This is because constant-time operations do not depend on n, and that growth is strictly slower than log n as n grows. Essentially, O(1) is a subset of o(log n).

Is there a difference if the logarithm base changes?

Changing the base of the logarithm amounts to a constant factor difference because log_a n = (log_b n) / (log_b a). For O() and o() notation, constant factors do not affect classification. So log base 2, log base 10, or natural log are equivalent in asymptotic terms.

Could you give an example where o(log n) might appear in real-world data structures?

In practice, truly sub-logarithmic operations can be found in certain specialized caches, hashing schemes, or approximate membership checks (e.g., Bloom filters) that can retrieve data in expected O(1) time. These expected O(1) lookups are also o(log n) because they grow more slowly than any constant multiple of log n. Another scenario is a parallel algorithm that uses many processors to split the workload so effectively that any single thread’s work becomes smaller than log n.

Are there any edge cases where an algorithm might theoretically be o(log n) but not practically faster?

Yes. Sometimes an algorithm might be described as o(log n) in a purely theoretical sense (for example, it might be O(log log n), which is indeed o(log n)), but the constants involved or the overhead might be large in practical situations. Additionally, specialized data structures or parallel approaches might have lower asymptotic complexity but high implementation complexity or hardware requirements.

How is o(log n) useful from an algorithmic standpoint?

Understanding that an algorithm’s runtime is o(log n) tells us its scaling cost is very minimal compared to typical logarithmic solutions (like balanced tree operations or binary searches). This can guide architectural and data structure choices, especially in large-scale systems or tight real-time constraints. It implies that as the input size doubles, the time complexity grows at a rate slower than the typical log n approach, often leading to substantial performance benefits for massive datasets.

Below are additional follow-up questions

What is the impact of hidden constants and lower-order terms in o(log n), and do they matter practically?

In theoretical computer science, hidden constants and lower-order terms are disregarded when stating o(log n). However, in real-world scenarios, these constants and smaller-order terms can sometimes dominate the actual runtime, especially for small to moderate input sizes. For example, an algorithm might theoretically have a sub-logarithmic growth, but if it uses expensive operations or large constant factors (e.g., initializing huge arrays, complex hashing schemes, or memory-intensive data structures), real performance might be worse than a simpler approach that is O(log n) in theory but has smaller hidden constants. Another subtlety is that hardware factors, such as CPU caches or vectorized instructions, can distort the theoretical analysis. An algorithm that’s sub-logarithmic in pure computation might have hidden memory latencies or require data transfers that don’t scale in the same way as the CPU instructions. This highlights why empirical testing is important, even if you’ve theoretically proven your algorithm is o(log n).

How do we validate or measure an algorithm’s o(log n) performance in practice?

To confirm that an algorithm exhibits o(log n) behavior, you would typically measure execution times (or operation counts) across various input sizes and then compare how those times grow relative to log n. If it’s truly sub-logarithmic, you should observe the measured growth curve flattening out more quickly than the log n reference line. A potential pitfall is not isolating other factors (like I/O overhead, memory caching, or background system processes) that can mask or distort the asymptotic growth pattern. In practice, you might conduct micro-benchmarks on controlled hardware while carefully measuring CPU cycles or instruction counts. Even then, real-world complexities—like branch prediction misses or context switches—can hide the true asymptotic behavior, so you should combine theoretical analysis with empirical experiments.

Can an algorithm that is o(log n) in the best or average case degrade to much worse complexity in the worst case?

Yes. An algorithm might appear sub-logarithmic under specific conditions or average-case assumptions, but when those assumptions fail, the worst-case complexity can jump considerably. For instance, certain hashing-based lookups are expected O(1) (which is o(log n)), but if hash collisions become frequent (e.g., due to adversarial inputs or poor hash functions), it can degrade to O(n). This discrepancy underscores the importance of analyzing both average and worst-case behavior. In performance-critical applications, you must ensure that pathological cases are either extremely rare or properly mitigated, otherwise an algorithm claimed to be o(log n) on average could degrade to something much larger in worst-case usage.

In which scenarios might you prefer an o(log n) algorithm over a standard O(log n) one in practical software designs?

Most standard balanced tree searches, binary searches, and sorting rely on O(log n) operations for each data access or insertion. If you can achieve a sub-logarithmic algorithm, that often indicates a specialized data structure or a specialized technique (e.g., an advanced hashing scheme, succinct data structure, or hardware-accelerated approach). You might prefer these designs if: • The dataset is extremely large and even small improvements over log n save considerable time at scale. • There are frequent queries requiring the absolute lowest latencies possible. • Hardware-specific optimizations (like GPU-accelerated approaches) benefit from limited memory transfers or sub-logarithmic traversal. A potential pitfall is over-optimizing with overly complex structures. Maintenance complexity, memory overhead, or concurrency considerations might outweigh the performance gains. So, you must weigh the operational cost and complexity of implementing sub-logarithmic designs against potential performance benefits.

How does parallelization influence sub-logarithmic algorithms?

Parallelization can reduce overall runtime if the workload can be divided effectively among multiple processors. In some cases, a task that’s O(log n) in a single-threaded environment can become O(log n / p) with p processors, or even O(1) if the computation can be perfectly split among all threads. In practice, perfect scaling rarely occurs due to synchronization overhead, communication costs, and load imbalances. For a sub-logarithmic algorithm, any overhead from thread management or inter-processor communication can become a dominant factor, negating the benefit of having an inherently small time complexity per operation. Achieving true sub-logarithmic performance in a parallel setting thus requires ensuring minimal lock contention, effective load balancing, and a data layout that avoids excessive cache coherence traffic. These subtle concurrency pitfalls can make or break the real-world performance of an algorithm touted as o(log n) in a purely sequential model.

Can sub-logarithmic data structures incur large unexpected overhead or performance bottlenecks?

Yes. Some data structures that offer sub-logarithmic operations rely on complex underlying mechanisms (like multi-level hashing, advanced tries, or compressed bit representations) which might demand large amounts of memory or preprocessing time. In distributed systems, sub-logarithmic query time might require sophisticated indexing or replication strategies, incurring heavy communication overhead or memory usage. One scenario is building a specialized skip index for sub-logarithmic query times in a search engine. If that index is very large, memory access patterns might cause cache misses, or network latencies might grow if the index is sharded incorrectly. While the local complexity might be sub-logarithmic, the end-to-end system could still suffer from high latency if the data is remote. Hence, engineers must consider overall system design, not just the standalone complexity class.

What trade-offs do engineers often make to achieve sub-logarithmic complexity?

Trade-offs can include: • Increased memory usage: Storing large hash tables, advanced indexes, or specialized data structures that trade space for time. • Preprocessing overhead: Building a sub-logarithmic index might demand heavy computation upfront. • Risk of pathological cases: Many data structures achieving near-constant or sub-logarithmic performance might degrade severely under adversarial inputs (e.g., hash collisions). • Implementation complexity: Sophisticated data structures can be error-prone to implement or maintain, making them less attractive if simpler O(log n) solutions are “good enough” in practice. When deciding if these trade-offs are worthwhile, developers must consider hardware constraints, time-to-market, future scalability, and the nature of the query patterns (e.g., read-heavy vs. write-heavy workloads). The bottom line is that real-world engineering is rarely driven by asymptotic complexity alone; memory limitations, concurrency demands, and maintainability often shape the final design choice.

What if a system’s constant factors make an o(log n) algorithm impractical?

Even though an o(log n) complexity suggests excellent scaling, big hidden constants or complicated logic can turn a theoretically efficient algorithm into a slow or resource-hungry one in practice. For example, a specialized data structure might require advanced bit-twiddling or compressing/uncompressing partial data repeatedly. As n grows extremely large, the sub-logarithmic asymptotic might eventually dominate, but for moderate ranges of n, simpler O(log n) methods could outperform it due to smaller overhead. In high-performance applications with real-time constraints, it’s common to benchmark multiple approaches with realistic input sizes. If a sub-logarithmic approach only outperforms others for extremely large n (beyond the operational range), it might be more pragmatic to choose a simpler, more predictable method. This is why analyzing real hardware performance curves is crucial: complexity notation is only one piece of the puzzle when building reliable and scalable systems.