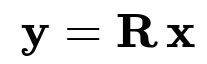ML Interview Q Series: What guidelines are followed when creating the random matrix for Gaussian Random Projection?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Gaussian Random Projection is a technique used to reduce the dimensionality of high-dimensional data by multiplying the data vectors by a randomly generated matrix whose entries typically come from a normal (Gaussian) distribution. The key principle is that certain geometric properties (like pairwise distances) can be approximately preserved under such a random linear map, as per the Johnson–Lindenstrauss lemma. In practice, this boils down to building a matrix with specific dimensions and sampling each entry from a Gaussian distribution, often with a mean of 0 and a variance chosen to balance distance-preserving properties.
Below is one of the most fundamental equations of random projection, capturing how a data vector x in R^d is projected to a lower-dimensional space in R^k:
Here:
x is a d-dimensional vector (original high-dimensional data).
R is the k x d random matrix (k < d in many use cases).
y is the k-dimensional projection (the output of applying Gaussian Random Projection).
In Gaussian Random Projection, each entry R_{i,j} is drawn from a normal distribution with zero mean and a variance that is chosen to preserve distances on average. A typical strategy is to scale the distribution by 1/sqrt(k) so that pairwise distances are not overly magnified or shrunk.
When constructing the random matrix for Gaussian Random Projection, the rules often include:
The shape of the matrix is k x d if we want to map d-dimensional points into a k-dimensional subspace.
Each entry is often sampled from N(0, 1/k). Sometimes, one may choose another variance factor, but 1/k is common.
The rows of the matrix are independently sampled from the same distribution, ensuring consistent statistical properties across all projected dimensions.
Mean 0 helps ensure that, on expectation, the projection is centered without introducing bias.
Proper variance scaling ensures that the expected length of projected vectors correlates reasonably with their original lengths, helping maintain relative distances.
Below is a small code snippet in Python using NumPy to illustrate how to create and apply such a Gaussian random projection matrix:
import numpy as np
# Suppose we have data in d dimensions and we want to project to k dimensions
d = 100 # original dimensionality
k = 20 # target dimensionality for projection
# Generate the random matrix R of shape (k, d), with entries from N(0, 1/k)
R = np.random.normal(loc=0.0, scale=1.0/np.sqrt(k), size=(k, d))
# Sample a random d-dimensional vector
x = np.random.rand(d)
# Project x into a k-dimensional space
y = R.dot(x)
print("Original vector (d-dimensional):", x)
print("Projected vector (k-dimensional):", y)
In this example, each element is drawn from N(0, 1/sqrt(k)^2). When you multiply the data vector x by the matrix R, you get a new vector y in k dimensions whose distance properties relative to other projected vectors can be approximately maintained.
Some additional considerations include ensuring k is large enough to preserve the distances you care about. The Johnson–Lindenstrauss lemma theoretically guides the choice of k in terms of how many points you have and how accurate you want to preserve distances. In practice, you may need to experiment with different values for k to find the right trade-off between dimensionality reduction and preserving the structure of your data.
What happens if we pick a different variance or scaling factor?
If you adjust the variance differently, the scale of projected vectors changes. This does not necessarily invalidate the random projection, but it can change the constant factors involved in distance preservation. The typical choice of 1/k is to keep the average projected length roughly on the same order as the original dimension, but you could also choose a different scaling if you have theoretical or empirical reasons.
How does the Gaussian random matrix preserve distances?
The formal justification comes from the Johnson–Lindenstrauss lemma, which states that a small number of random projections can preserve pairwise distances between points within a small multiplicative error, as long as the data does not contain too many points relative to k. Intuitively, random directions in high-dimensional spaces tend to be orthogonal or near-orthogonal, so when you multiply by a suitably scaled matrix, pairwise distances do not collapse or expand too drastically.
Are there any practical issues with very large datasets?
One drawback is that Gaussian random projection can be expensive when d is large, because creating a full k x d matrix and applying it can require a lot of memory and computation. Methods like Sparse Random Projection or structured random matrices (e.g., using the Fast Johnson–Lindenstrauss Transform) help mitigate this cost by storing fewer non-zero entries or using fast transforms.
What if the data is highly sparse?
When data is extremely sparse, standard Gaussian random projection might destroy sparsity because every projected coordinate can become non-zero. Sparse Random Projection is often used in such cases, because it ensures that many of the elements in the random matrix are zero, thereby preserving some of the sparse structure while still maintaining distance-preserving properties.
Could we use a distribution other than Gaussian?
Yes. In fact, the Johnson–Lindenstrauss lemma does not require a strictly Gaussian distribution; it only requires a sub-Gaussian or suitable distribution that satisfies certain concentration properties. Uniform or certain sparse distributions also work. The Gaussian choice often simplifies mathematical analysis and is widely used in practice.
How do we select k in practice?
The lemma itself provides a theoretical bound on k in relation to the number of data points (n) and the desired error in distance preservation (epsilon). A simplified version often looks like k ~ O(log n / epsilon^2). In practice, you might try values of k and measure how your application’s performance (e.g., classification accuracy, clustering quality) is affected by the dimensionality reduction. Balancing memory usage, computational efficiency, and accuracy is key.
Are there any steps to validate or test the quality of a random projection?
A common strategy is to:
Compare pairwise distances (or a representative sample) before and after projection.
Check if the distortion remains within acceptable limits for your task.
Evaluate your end-to-end pipeline (classification, regression, clustering, etc.) on the projected data to see if performance metrics hold up.
What kinds of data are best suited for Gaussian Random Projection?
Gaussian random projection is quite general and can be applied to dense or moderately sparse data. For extremely high-dimensional and very sparse data, one might consider other methods like hashing-based techniques or Sparse Random Projection to exploit the data’s structure and reduce computation.
These considerations form the basis for using Gaussian Random Projection in real-world scenarios. By following the guidelines—using a matrix of appropriate size, carefully chosen variance, and validating performance—one can harness the benefits of this powerful dimensionality reduction technique.