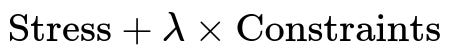ML Interview Q Series: What is Multidimensional Scaling?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Multidimensional Scaling (MDS) is a class of techniques that aims to embed high-dimensional data points into a lower-dimensional space while preserving the pairwise distances (or dissimilarities) among the points as faithfully as possible. The basic idea is that we have a set of data points in some original space, and we know or can compute a measure of dissimilarity between every pair of these points. We want to place these points into a space of lower dimension—often 2D for visualization—such that the distances in the reduced-dimensional representation reflect the original dissimilarities.

MDS comes in different flavors, notably metric (classical) MDS and non-metric MDS. Metric MDS tries to preserve the actual numerical distances, whereas non-metric MDS focuses on preserving the rank-order relationships of those distances. In classical metric MDS, distances are processed via an eigen-decomposition-based approach closely related to Principal Component Analysis. In non-metric MDS, an iterative procedure optimizes an objective function (often called a stress function) that measures the discrepancy between distances in the embedded space and the original pairwise distances.

One of the most common forms of the cost or stress function used in MDS is formulated to measure how well the distances in the embedded space match the original distances. A well-known example of a stress function is shown below.

Here, d_{ij} represents the distance between points i and j in the lower-dimensional embedding, and delta_{ij} represents the dissimilarity (or distance) between points i and j in the original space. The numerator sums the squared differences between d_{ij} and delta_{ij}, and the denominator is a normalization factor to scale the result.

When solving an MDS problem, one typically:

• Computes the pairwise distance (or dissimilarity) matrix from the high-dimensional input data or from any given distance metric. • Chooses a target dimensionality, often 2 for visualization or for obtaining compact features. • Initializes the lower-dimensional coordinates (possibly randomly). • Iteratively optimizes an objective (stress) function by adjusting the coordinates in the lower-dimensional space to bring d_{ij} as close as possible to delta_{ij}.

Classical (metric) MDS uses a closed-form solution under the assumption that the dissimilarities can be directly interpreted as Euclidean distances. Non-metric MDS uses iterative methods (e.g., SMACOF) to preserve the rank ordering of distances.

MDS is frequently used in exploratory data analysis, psychological research, and other fields where the goal is to visualize similarities or dissimilarities between objects (e.g., users, products, documents) in a two-dimensional or three-dimensional plot. It differs from techniques like PCA because PCA seeks directions of maximum variance based on covariance structure, whereas MDS focuses directly on preserving pairwise distances and can use non-Euclidean dissimilarities.

How it Differs from Other Dimensionality Reduction Methods

PCA relies on the covariance matrix and linear projections, producing embedding directions of greatest variance. If the original notion of distance is non-Euclidean or if only pairwise dissimilarities are available (with no direct feature vectors), PCA cannot straightforwardly be applied, whereas MDS can. Additionally, non-metric MDS can handle data for which we only have an ordinal ranking of distances, which is something that standard PCA cannot do.

Computational Considerations

When the dataset is large, storing and processing the entire pairwise distance matrix can be computationally expensive (memory usage grows with the square of the number of data points). Iterative algorithms may become slow. In practice, approximate or stochastic methods can be used to deal with large datasets. Ensuring global optima can be challenging as well, because stress functions can have multiple local minima.

Follow-up Questions

What is the difference between metric and non-metric MDS?

Metric MDS assumes that the original distance measures are true metric distances, and it tries to preserve these distances in the lower-dimensional embedding. This usually involves a direct relationship between the distances in the original space and the distances in the embedded space. Classical MDS, for example, uses eigen-decomposition of a transformed distance matrix to obtain the embedding in one shot.

Non-metric MDS only tries to preserve the rank order of the distances rather than the distances themselves. For example, if delta_{ij} < delta_{kl} in the original dissimilarity matrix, then in the embedded space we want d_{ij} < d_{kl}. The exact numerical values of d_{ij} do not matter as much as their ordering. This form of MDS is more flexible when the data contains only ordinal information or less precise distance measures.

How do we compute distances for MDS when the original data is high-dimensional?

If the original data is given as vectors in a high-dimensional space, we typically compute pairwise distances using a standard metric, such as Euclidean distance or sometimes Manhattan distance. Each pair of vectors x_i and x_j is processed to obtain a single number that represents delta_{ij}, the dissimilarity. These values populate a distance matrix, which MDS then uses.

For non-Euclidean data (like graphs or abstract similarity measures), one can define a custom distance function or domain-specific dissimilarity. MDS does not require an explicit vector space as input; it only needs a complete pairwise dissimilarity matrix.

When might MDS produce undesirable embeddings?

If the dissimilarity matrix is not Euclidean or contains errors/noise (for example, some distances might violate the triangle inequality), then a low-dimensional Euclidean embedding might not exist or might produce severe distortions. Furthermore, iterative optimization can get stuck in local minima if the data is complex. Large datasets and high noise levels can also make convergence to a good global solution difficult, so the final embedding may not faithfully preserve the original distances.

Why is the normalization factor in the stress function necessary?

In the stress function, we often divide by the sum of the squared original distances to scale the stress value into a dimensionless measure, making it easier to compare solutions across datasets of different scales. Without normalization, large scale distances would produce large raw stress values even if the relative differences were quite small.

What is the relationship between classical MDS and PCA?

Classical MDS, when based on Euclidean distances, can be shown to be equivalent to PCA in the sense that the embedding coordinates given by classical MDS are related to the top principal components extracted from the data’s Gram matrix (which is derived from the pairwise distances). In classical MDS, one transforms the distance matrix into a Gram matrix using double centering and then performs an eigen-decomposition. This process parallels PCA’s computation using a covariance matrix, but from the perspective of distances instead of raw data features.

How do we implement a simple MDS algorithm in Python?

A straightforward way to do classical MDS is to compute the distance matrix, convert distances into a Gram matrix, and then perform an eigen-decomposition. Here is an illustrative Python snippet. This is not production-ready code, but it outlines the basic approach for classical MDS.

import numpy as np
from scipy.spatial.distance import pdist, squareform

def classical_mds(data, dim=2):
    # data is assumed to be an array of shape (n_samples, n_features)
    # Step 1: Compute distance matrix
    D = squareform(pdist(data, metric='euclidean'))

    # Step 2: Convert D to a Gram matrix using double centering
    n = D.shape[0]
    J = np.eye(n) - np.ones((n, n)) / n
    B = -0.5 * J @ (D**2) @ J

    # Step 3: Eigen-decomposition of B
    eigenvals, eigenvecs = np.linalg.eigh(B)

    # Sort eigenvalues in descending order
    idx = np.argsort(eigenvals)[::-1]
    eigenvals = eigenvals[idx]
    eigenvecs = eigenvecs[:, idx]

    # Step 4: Select top 'dim' dimensions
    # Take only the positive eigenvalues
    positive_eigenvals = np.maximum(eigenvals[:dim], 0)
    coords = eigenvecs[:, :dim] * np.sqrt(positive_eigenvals)

    return coords

# Example usage:
if __name__ == '__main__':
    # Suppose data is 10 samples in a 5D space
    np.random.seed(42)
    X = np.random.rand(10, 5)
    embedded_coords = classical_mds(X, dim=2)
    print("Lower dimensional coordinates:\n", embedded_coords)

One can adapt more advanced (non-metric) MDS algorithms by replacing the direct eigen-decomposition with an iterative process (like SMACOF) that tries to minimize the stress function.

How to deal with missing distances in MDS?

If the distance matrix is incomplete, classical MDS cannot be applied in its standard form, because the eigen-decomposition needs a full matrix. For non-metric MDS, there are iterative approaches that can be adapted to skip or impute missing values, penalize unknown distances, or incorporate specialized routines that only sum over known distances. These approaches often require custom modifications to the stress function or to the optimization routine.

Potential pitfalls and edge cases

If the data has outliers or extremely large distances, they can dominate the stress function and produce suboptimal embeddings. Preprocessing or outlier detection methods can help. Also, if the target dimensionality is too low compared to the complexity of the original data, the embedding may be unable to preserve distance relationships, leading to high stress values. Finally, when implementing MDS at scale, storing a large distance matrix (size n x n) can exceed memory limits for large n, requiring approximate or incremental methods.

Below are additional follow-up questions

Could you elaborate on the difference in local vs. global structure preservation, and how MDS handles each?

Multidimensional Scaling (MDS) can, in principle, preserve both local and global distances across the entire dataset. The term “local structure” usually refers to the small inter-point distances among neighbors, while “global structure” refers to the overall distances across all points in the dataset.

In classical (metric) MDS, the objective function tries to preserve the absolute pairwise distances. Therefore, the global structure—where points that are far apart must remain far apart in the lower-dimensional embedding—tends to be faithfully represented if the data naturally lives in a low-dimensional Euclidean space. However, if the dimensionality of the underlying manifold is high or the distances cannot be perfectly embedded in a smaller space, global distances can be distorted. Local distances might still be relatively well-preserved, but classical MDS does not focus exclusively on neighborhood relationships.

In non-metric MDS, since the stress function focuses on preserving rank order of distances, local neighborhoods and global relationships both matter in how the points are spread out. Local distances that are ranked smaller should remain among the smallest in the final embedding, and likewise for larger distances. Problems can occur if the data manifold is extremely complex and cannot be captured in just a few dimensions. Then, trade-offs will arise where some local neighborhoods are distorted to achieve better global embedding, or vice versa.

Potential Pitfalls and Edge Cases: • High-variance data can pull apart points in a way that preserves large-scale distances at the expense of local structure. • If the data truly has local manifold geometry (like in some image or text embeddings), MDS may fail to capture subtle local neighborhoods. Methods such as t-SNE or UMAP may be more appropriate if local neighborhoods are the key focus. • Large amounts of noise or outliers can disrupt the global geometry, skewing the embeddings so that local relationships become overshadowed.

Are there any domain-specific applications or modifications that might be needed for MDS in specialized fields?

Different fields, like bioinformatics, text analysis, and image processing, often have specialized distance measures or domain constraints. In some cases, we do not simply use Euclidean distance but incorporate problem-specific definitions of similarity or dissimilarity.

In genomics or proteomics, for example, the distance might be defined in terms of sequence alignment scores rather than geometric distances. In text or document clustering, the distance might come from cosine similarity or a custom word-mover distance. MDS then needs these domain-specific distances as input.

Additionally, certain fields require constraints on how the embedding should look. For instance, in psychology or marketing research, we might know that certain items cannot be placed too closely because they represent conceptually distinct categories. One can then modify the stress function or add penalty terms to enforce these constraints.

Potential Pitfalls and Edge Cases: • Using a non-metric distance (e.g., alignment scores) in classical (metric) MDS can lead to negative eigenvalues in the derived matrices, potentially invalidating a direct eigen-decomposition. • Domain constraints that conflict with natural distances can make optimization more difficult, sometimes causing the iterative MDS process to fail to converge or to converge to suboptimal embeddings. • If the user lacks sufficient domain knowledge to define an appropriate distance metric, MDS may produce misleading visualizations or clusters.

How does MDS compare with t-SNE or UMAP for data visualization tasks?

MDS, t-SNE, and UMAP all aim to project high-dimensional data into a lower-dimensional space, often for visualization purposes, but they emphasize different aspects of the data.

• MDS tries to preserve pairwise distances (metric MDS) or at least rank orders (non-metric MDS) as faithfully as possible. It places equal emphasis on both global and local distances. • t-SNE focuses heavily on preserving local neighborhoods. Points that are close in the high-dimensional space remain close in the embedded space, but global relationships may be less obvious. t-SNE also has parameters (perplexity, learning rate, etc.) that can significantly alter the result. • UMAP also emphasizes local structure while trying to preserve more global aspects than t-SNE. It uses a graph-based approach and can generate more interpretable global structures in many cases, though it is still primarily local-neighborhood-oriented.

Potential Pitfalls and Edge Cases: • MDS can struggle with complex manifolds where local structure is more informative than global distances. • t-SNE can produce visually appealing clusters that may obscure large-scale relationships or appear to form discrete clusters even when the data is more continuous. • UMAP can sometimes create “artificial gaps” or distort distances if parameter tuning is not carefully done. • Choosing the wrong method can lead to misleading conclusions about how the data clusters or how points relate to each other.

Could you discuss strategies for choosing the dimension for embedding in MDS?

Deciding on the target dimensionality is largely driven by the intended application. For visualization, 2D or 3D is common. For feature reduction, higher dimensions might be chosen (e.g., 10, 20) to feed into downstream algorithms while preserving distances.

Common strategies include: • Elbow method on the stress curve: Evaluate the MDS stress (or related measure) for different target dimensions and see if there is a clear “elbow” beyond which increasing dimensions yields diminishing returns in stress reduction. • Cross-validation: If you can define a predictive task or a reconstruction objective, you may choose the dimensionality that best preserves performance or reconstruction accuracy. • Domain knowledge: Knowing that the data likely has a low intrinsic dimensionality (e.g., manifold dimension ~10) can guide the embedding choice.

Potential Pitfalls and Edge Cases: • Overestimating the dimension can lead to overfitting: the distances might appear perfectly preserved, but the embedding could be too large to interpret meaningfully. • Underestimating the dimension can yield a high-stress solution that does not reflect the original distances well, potentially causing clusters or structures to collapse. • The chosen dimension may fail to highlight important features if domain knowledge is overlooked.

Is it possible to incorporate additional constraints or side information into MDS, such as grouping constraints or partial label information?

Yes. One can modify the stress function to include penalty terms that encode side information. For instance, if certain points belong to the same class, one might add constraints to pull them closer together, or if certain points must remain apart, add penalties for small distances between them.

An example is Constrained MDS, where the objective is:

In inline text: The constraints can be a sum of violation terms for points that must be closer or farther based on side knowledge. A higher lambda emphasizes the constraints more than the raw distance preservation.

Potential Pitfalls and Edge Cases: • Overconstraining the problem can make the solution infeasible or lead to embeddings that respect constraints but fail to preserve the original distances well. • Balancing the weight of constraints is tricky: a small lambda might be ignored by the optimization, while a large lambda can dominate the stress function. • Incorporating partial label information may inadvertently distort the distances among unlabeled points if the constraints are not designed carefully.

How do we properly interpret MDS plots in real practice, and what are some common pitfalls when drawing conclusions?

Interpretation of MDS plots requires caution and context: • Clusters in an MDS plot suggest that these points are similar or close in the original dissimilarity measure, but MDS can compress or stretch certain regions to fit into a low-dimensional space. • Axes in an MDS plot are not necessarily aligned with any meaningful direction like in PCA, because MDS simply places points to minimize overall stress. Hence, axis labels usually do not have an intrinsic interpretation. • Proximity in the embedded space indicates relative similarity if the stress is low. However, if the stress is high, many distances are distorted, making close or distant pairs less reliable.

Potential Pitfalls and Edge Cases: • Over-interpreting the axes and concluding that “the x-axis represents feature A and the y-axis represents feature B” is incorrect unless you have strong domain evidence. • If the stress is high, the embedding might visually show clusters that do not accurately reflect the original high-dimensional relationships. • Outliers in the original data can dramatically shift the arrangement of other points, as MDS tries to accommodate very large distances for outliers. • If the data is highly non-Euclidean or violates fundamental distance properties, the embedded plot can be misleading, and standard MDS may not be suitable.