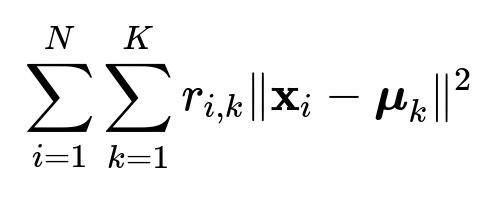ML Interview Q Series: What is the primary reason that k-Means typically relies on Euclidean distance as its preferred measure?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
k-Means Clustering seeks to minimize the total squared distance between each data point and its assigned cluster centroid. The Euclidean distance arises naturally when the goal is to reduce this sum of squared deviations. In more detail, the standard k-Means objective function is:
Here N is the total number of data points, K is the number of clusters, r_{i,k} is an indicator that is 1 if point x_i is assigned to cluster k and 0 otherwise, x_i denotes the ith data point, and mu_k is the centroid of cluster k. The notation ||x_i - mu_k|| refers to the Euclidean norm of the difference between x_i and mu_k.
Minimizing this objective with respect to the cluster centroids mu_k and the assignments r_{i,k} involves solving two subproblems iteratively:
Assignment step: Assign each point to the centroid to which it is closest in terms of Euclidean distance.
Centroid update step: Compute each new centroid as the mean of points currently assigned to it.
The use of Euclidean distance ties neatly into these updates. Specifically, the best centroid (in a least-squares sense) is the mean of the points that belong to that cluster if the distance is Euclidean. This direct relationship between the arithmetic mean and the Euclidean norm makes k-Means algorithmically straightforward and computationally efficient in practice.
Additionally, k-Means relies on the geometry of the Euclidean space, making it simple to compute gradient-like directions for minimization. The Euclidean distance squared is both smooth and differentiable in terms of the centroid, facilitating the straightforward update rule. While other distance metrics can be applied, the connection with the simple mean update step is lost or becomes more complex, and it often requires specialized modifications to the core algorithm.
Why is Euclidean Distance Preferred Over Other Metrics in k-Means?
The arithmetic mean is the minimizer of sum of squared Euclidean distances.
The objective function with squared Euclidean distances is differentiable, enabling neat centroid updates.
Many implementations and libraries are optimized for this distance, contributing to its widespread usage.
Potential Follow-Up Questions
How do you initialize centroids in k-Means, and why is this important?
If initial centroids are chosen randomly, the algorithm can converge to suboptimal (local) minima. This is because k-Means is sensitive to the initial cluster assignments. Popular strategies like k-Means++ attempt to choose initial centroids far apart by selecting the first centroid randomly, then weighting subsequent centroid choices by the square of their distance to existing centroids. This helps the algorithm converge more reliably and reduces the chances of poor local optima.
Is k-Means guaranteed to find the global optimum?
k-Means typically converges to a local minimum, not necessarily the global minimum of the objective function. This local optimum depends on the initial placement of centroids. While each iteration of the assignment-update steps will decrease (or keep unchanged) the objective function, there is no guarantee that the result will be the global best solution. Hence, people often run k-Means multiple times with different initial centroids to pick the best outcome among various runs.
Can we use other distance metrics in k-Means?
You can, but then the centroid update step might not be the simple arithmetic mean. For example, if one chooses a Manhattan distance, the optimal centroid becomes the median, not the mean. This results in an algorithm that is no longer precisely “k-Means” but rather a k-Medians or k-Medoids approach. Such variants are often more robust to outliers but can be more computationally expensive and may lose some of the neat mathematical properties of the Euclidean-based algorithm.
How does the presence of outliers affect k-Means?
Outliers can disproportionately skew the mean, because the arithmetic mean is highly sensitive to extreme values. A single outlier can shift a cluster centroid significantly away from the center of mass of the remaining points. For datasets with many outliers or heavy-tailed distributions, techniques like k-Medians, k-Medoids, or clustering algorithms with more robust distance metrics might be more suitable. One can also use data pre-processing methods like outlier removal or robust scaling before applying k-Means.
What is the computational complexity of k-Means?
A single iteration of the algorithm requires assigning N data points to their closest centroid among K clusters, which is O(N*K). Then, updating each of the K centroids by computing an average of the assigned points is O(N) if the points are already grouped. The algorithm typically converges in a finite number of iterations, but the number of iterations can vary. Although k-Means can be relatively fast, for very large N or very high dimensional data, one may need efficient extensions like mini-batch k-Means or approximate nearest centroid searching.
When might you prefer a different clustering approach?
If you need to cluster data that is not well-separated in Euclidean space or has complex geometrical shapes (e.g., non-convex), density-based methods like DBSCAN can be more suitable.
If your data contains many outliers, median-based clustering approaches like k-Medians might be better.
If the number of clusters is unknown or if you want to detect variable cluster densities, hierarchical or density-based methods might be preferred.
These considerations reflect how fundamental Euclidean distance is to standard k-Means and why that particular metric aligns so well with the arithmetic mean update procedure.