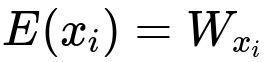ML Interview Q Series: What is the primary purpose of adding an Embedding Layer to a neural network, and what key benefits does it offer?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
An Embedding Layer is commonly used to convert discrete categorical variables—especially words or tokens—into dense, continuous vector representations. This transformation is particularly useful in natural language processing (NLP) tasks, but it can also be applied to recommenders and other domains that involve large vocabularies of categorical features. The layer is learned end-to-end along with the rest of the neural network, allowing it to capture semantic or task-specific relationships in a compact, low-dimensional space.
Dense Representation Versus One-Hot Encoding
A typical approach for categorical data might involve a one-hot encoding that creates a sparse vector for each item in a vocabulary. Such vectors often become very large, especially when dealing with extensive vocabularies, and they do not reflect any notion of similarity between tokens. With an Embedding Layer, each token (e.g., each word) is mapped to a learned embedding vector in a lower-dimensional, continuous space. Embeddings that end up being close together in this space are often semantically or contextually related.
Core Mathematical Operation of an Embedding Layer
Below is the fundamental formula for an embedding lookup, where W is the embedding matrix, x_i is the discrete index of the i-th token, and E(x_i) is the resulting embedding vector.
Here W_{x_i} refers to the row of the embedding matrix W corresponding to the index x_i. The embedding matrix W typically has the shape (vocab_size, embedding_dim). The vocabulary size is the total number of unique tokens, and embedding_dim is the dimension of the dense vector space into which each token is projected.
How the Embedding is Learned
The embedding vectors are optimized during training by backpropagation. The network adjusts these vectors so they become more effective for the specific predictive or classification task. Over the course of training:
Tokens that appear in similar contexts or share some functional similarity in the training data tend to develop embeddings that are close to each other in the embedding space.
The dimensionality of the embedding layer (embedding_dim) is often much smaller than the vocabulary size, leading to a more compact representation than one-hot vectors.
Practical Implementation Example
Below is a brief snippet in PyTorch showing how to define and use an embedding layer for a vocabulary of size 1000, mapping each token to a vector of size 64.
import torch
import torch.nn as nn
vocab_size = 1000
embedding_dim = 64
embedding_layer = nn.Embedding(num_embeddings=vocab_size, embedding_dim=embedding_dim)
# Suppose we have a batch of token indices
token_indices = torch.LongTensor([10, 20, 30, 999])
embedded_output = embedding_layer(token_indices)
print(embedded_output.shape)
# Output might be: torch.Size([4, 64]) -> 4 tokens each mapped to a 64-dimensional vector
The nn.Embedding layer learns a matrix of shape [vocab_size, embedding_dim]. During the forward pass, it looks up the row in that matrix corresponding to each token index.
Advantages of Using an Embedding Layer
There is a compression advantage, where each token is represented in a small dimensional space rather than a massive sparse one-hot vector. More importantly, the learned embeddings preserve semantic relationships, so tokens with related contexts end up being close in the embedding space. This aspect is crucial for capturing patterns in language models and other tasks.
How Do You Choose the Dimensionality of an Embedding Vector?
One common approach is to pick an embedding dimension that balances model capacity and computational efficiency. If the dimension is too large, the model might overfit and become too large to handle. If it is too small, it might not capture enough information about each token. Practitioners often select dimensions in ranges like 50 to a few hundred, although this varies widely depending on the dataset size, the complexity of the language or items, and the available computational resources.
How Do You Handle Tokens Not Seen During Training?
Real-world applications often face out-of-vocabulary (OOV) tokens. One strategy is to have a special "unknown" or "UNK" token. During inference, any token that was not part of the training vocabulary is mapped to this token's embedding. Another strategy is to use subword tokenization (e.g., Byte-Pair Encoding, WordPiece) so that rare or novel words can be decomposed into smaller units that already appear in the embedding matrix.
Why Not Just Use One-Hot Encodings and Rely on a Fully Connected Layer?
One-hot representations are often extremely large and sparse for big vocabularies, which leads to high-dimensional parameter spaces and inefficient training. An Embedding Layer essentially does a matrix multiplication with a one-hot vector internally but stores it in a trainable and compact form. This allows for significantly fewer parameters and captures the relationships between tokens in a more nuanced way.
Can You Use Pretrained Embeddings?
Pretrained embeddings (like GloVe or Word2Vec) can be loaded into the Embedding Layer weights before training. In many frameworks, you can initialize nn.Embedding with a matrix of pretrained vectors and choose whether to keep them frozen or allow further fine-tuning. This is especially helpful when you have limited data, because the pretrained embeddings may already encode rich semantic information from large unsupervised corpora.
What Are Potential Pitfalls When Using an Embedding Layer?
Memory constraints can arise when dealing with extremely large vocabularies. You may need to reduce the vocabulary size by filtering out very rare tokens or use subword/tokenization methods. Another concern is that if your training data does not have good coverage of the vocabulary, some embeddings may not be trained effectively and might not carry meaningful representations.
How Does an Embedding Layer Impact the Overall Model?
The embedding vectors become the first level of representation in many NLP models, shaping how the tokens are perceived by deeper layers like LSTMs, GRUs, Transformers, or fully connected networks. If the embeddings are well-initialized and well-trained, they can greatly improve the convergence and the final performance of the entire model. If they are poorly trained or too limited in dimension, they may bottleneck the entire architecture.
Below are additional follow-up questions
How do you decide whether to freeze or fine-tune an Embedding Layer in a transfer learning scenario?
Freezing the layer means you keep the embedding weights fixed after initializing them (often with pretrained vectors), while fine-tuning allows the backpropagation algorithm to update them during training. Freezing can be beneficial if you have:
Limited training data: This avoids overfitting your embeddings to a small dataset.
Strongly trusted pretrained weights: For example, if they come from very large corpora and already capture the nuances of your language domain.
However, fine-tuning can be advantageous if you have:
Sufficient data: Enough to adjust embeddings to your specific downstream task.
A domain that differs from the original pretraining domain: E.g., biomedical text vs. general English text. The embeddings might need to be adapted to specialized language.
A potential pitfall is overfitting: if the dataset is small and you still decide to fine-tune, you might adapt the embeddings too specifically to the training set. Conversely, if you keep embeddings frozen in a scenario where your domain is drastically different, you might never learn domain-specific representations. A balanced approach sometimes involves fine-tuning only part of the embedding layer or using a smaller learning rate for the embeddings compared to the rest of the network.
How do you handle scenarios where multiple categorical features, not just tokens, must be embedded simultaneously?
Some real-world applications involve multiple categorical features, such as user IDs, item IDs, or other metadata, in addition to text tokens. You can maintain separate Embedding Layers for each feature type. This means each feature has its own embedding matrix, and you can either concatenate or sum these embeddings for the final representation. For instance, a recommender system might embed both users and items and then combine these embeddings in a predictive model.
Pitfalls include misalignment of embedding dimensions if you try to combine them in a naive way. Typically, you ensure each feature embedding has the same dimension if you plan to sum or concatenate them in a consistent manner. Also, careful feature engineering and data cleaning are required because embedding multiple categorical features can lead to a significant increase in total parameters.
What strategies can be used to deal with homonyms or words with multiple meanings within an Embedding Layer?
A single word index in a standard embedding matrix typically corresponds to one embedding vector, regardless of multiple meanings. This can be problematic if a word like “bank” can refer to a financial institution or a riverbank, causing the embedding to be an average representation of multiple contexts.
Possible strategies include:
Contextual Embeddings: Approaches like BERT or GPT produce context-dependent vectors, effectively assigning different embeddings for the same token in different contexts.
Subword/Character Embeddings: Breaking words into smaller units can help distinguish subtle morphological cues.
Word Sense Disambiguation Preprocessing: Identifying the sense of a word in context before using a more traditional embedding can yield more accurate representations.
A major edge case arises in highly specialized domains or languages with many polysemous terms. In such cases, purely static embeddings might fail to capture the intricacy of meaning variations.
How do you interpret or visualize learned embeddings to ensure they are meaningful?
Common methods include dimensionality reduction techniques such as t-SNE or UMAP to project the high-dimensional embeddings down to 2D or 3D space so you can visually inspect clusters of related tokens. You might see synonyms or thematically related tokens co-located.
A subtle pitfall is over-interpretation. Clusters may appear coherent in a 2D projection but could be artifacts of how t-SNE or UMAP compress the data. Also, while visualization can offer insights, it does not provide a definitive measure of how well embeddings perform for a given predictive task. For thorough understanding, combine visualization with quantitative evaluations like word similarity metrics or downstream task performance.
In what ways can an Embedding Layer cause training instability, and how would you mitigate it?
An Embedding Layer, like any parameterized layer, can sometimes lead to unstable gradients, especially when dealing with very large vocabularies or high embedding dimensions. If the initialization is poor, gradients can explode or vanish, slowing or halting training.
Mitigation techniques include:
Proper Initialization: Ensure the weight matrix is initialized with a method that keeps gradients well-scaled (e.g., Xavier or Kaiming initialization if supported by the framework).
Gradient Clipping: Especially if you have an RNN/Transformer downstream, clipping large gradients can keep training stable.
Lower Learning Rates for Embeddings: Sometimes you can use a different (often smaller) learning rate for the embedding layer to avoid large, erratic updates.
Edge cases might arise if the embedding dimension is excessively large or the vocabulary is extremely broad with many rarely seen tokens. Uncommon tokens might have embeddings that barely get updated, ending up undertrained or random.
How do you address catastrophic forgetting in embeddings when continuously training on new data?
Catastrophic forgetting occurs when embeddings learned on initial training examples degrade upon exposure to new data from a different domain or distribution. This is especially relevant in continual or incremental learning setups. Strategies for mitigating this include:
Regularization: Techniques like Elastic Weight Consolidation (EWC) can help preserve important parameters from older tasks by penalizing large shifts in weights that are crucial for previously learned knowledge.
Replay Buffers: Keep a portion of past training examples in memory and interleave them with new data to maintain performance on older distributions.
Gradual Unfreezing: Start by keeping embeddings frozen and only begin fine-tuning them slowly as you introduce new data, so you do not drastically alter representations for older examples.
Potential pitfalls include increased computational overhead with replay strategies or not sufficiently adapting if the new domain differs substantially, which might then require a more aggressive fine-tuning of the embeddings.
How might Embedding Layers be leveraged in non-NLP contexts, and what are the risks?
Embedding Layers are also popular for categorical features in fields like recommender systems, ad-click prediction, and graph representation. You can embed user IDs, product IDs, ad IDs, and so forth. This transforms large discrete ID spaces into learned representations that capture user-product or user-user relationships.
Risks include:
Overfitting: If each user ID is assigned a unique embedding but has few interactions, the model may overfit these sparse IDs.
Memory Constraints: Embedding matrices can become very large if you have tens of millions of users or items.
Cold Start Problem: New users or items not seen at training time might not have meaningful embeddings. You often address this by fallback strategies or user feature embeddings (e.g., demographic info).
Edge cases are especially prominent when the distribution of user/item interactions is skewed. Popular items get heavily trained embeddings, while rarely accessed items remain poorly represented.
What is the difference between factorizing the output layer versus using an Embedding Layer for inputs in language models?
In large language models, it is common to mirror the input embedding matrix in the output layer for efficiency. You essentially project the hidden states back to the vocabulary space for predictions. This approach is sometimes referred to as tying the input and output embeddings so they share weights.
Potential advantages include:
Reduced parameter count: Instead of having two separate large matrices, you reuse the embeddings.
Consistency in representation: The same learned subspace for both input tokens and output predictions can help the model converge better.
However, a potential downside is that the constraints of a shared embedding can limit the expressiveness of the output projection. If your input embeddings need to capture certain nuances differently than what the output layer demands, tying them might be suboptimal. This limitation may become more pronounced if your vocabulary or domain changes after initial training.
How can you integrate embedding dropout and what does it achieve?
Embedding dropout randomly zeroes out entire embedding vectors (rather than individual elements, as done in standard dropout). This forces the model to avoid over-reliance on a single token’s embedding during training. It is commonly used in sequence models like RNNs or Transformers to improve generalization.
Pitfalls include:
Overly aggressive dropout can erase too many embeddings, making the training signals noisy and potentially harming convergence.
Underusing dropout in extremely large models might miss out on a beneficial regularization technique, especially if the model has a tendency to memorize certain tokens.
A balanced approach is to incrementally tune the dropout rate. Start small and gradually increase if signs of overfitting are observed.