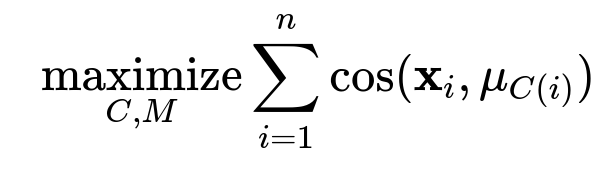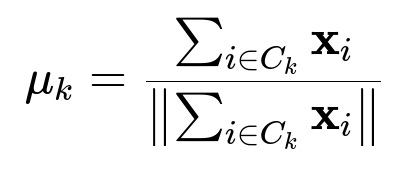ML Interview Q Series: What is the mechanism behind Spherical k-Means when handling data with very high dimensionality, particularly text data?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Spherical k-Means is an adaptation of the traditional k-Means clustering approach designed to work more effectively with data for which directional similarity is more meaningful than Euclidean distance. It is particularly useful in high-dimensional text data (e.g., documents represented as TF-IDF vectors). In text data, the magnitude of feature vectors often varies widely, so focusing on their direction rather than raw Euclidean distance can better capture semantic similarity.
Whereas standard k-Means minimizes the sum of squared Euclidean distances between points and their assigned centroids, Spherical k-Means aims to group points based on cosine similarity or equivalently angular distance. Before the clustering process, each data vector is usually normalized to have unit length, converting them into points on a unit hypersphere. Each centroid is similarly normalized after each update step, ensuring it remains on the unit sphere.
Core Mathematical Details
Below is a commonly used objective function for Spherical k-Means, where it attempts to maximize the total cosine similarity between each data point and its respective cluster centroid:
Here:
n is the total number of data points.
x_i is the i-th data vector (already normalized to unit length).
C(i) is the index of the centroid to which x_i is assigned.
mu_{C(i)} is the centroid (also normalized to unit length) of the cluster assigned to x_i.
cos(a, b) denotes the cosine similarity between vectors a and b, which is (a dot b) / (||a|| * ||b||).
The centroid update in Spherical k-Means also involves normalization to ensure each centroid remains on the unit hypersphere. For the k-th cluster, the centroid update often looks like this:
where:
C_k is the set of data point indices belonging to the k-th cluster.
x_i is the i-th data vector, assumed to be normalized.
mu_k is the normalized mean vector, representing the direction of the cluster k.
When the vectors are on the unit sphere, this update rule ensures that the new centroid remains on the sphere, making the algorithm focus on directions of vectors rather than raw magnitude.
Why Spherical k-Means Is Suitable for Text
Text data often has very high dimensionality, where each dimension corresponds to a word or token in the vocabulary. Such vectors can be extremely sparse, and their magnitudes may not be as informative as their direction. For instance, two documents can have different overall lengths but may still be topically similar if they share many of the same terms, albeit in different absolute frequencies. By normalizing each document vector, Spherical k-Means effectively factors out differences in length or magnitude and focuses on whether two documents share similar “directions” in the high-dimensional feature space.
Practical Implementation
The general steps for Spherical k-Means are:
Normalize each data vector to unit length.
Initialize cluster centroids (e.g., randomly select points as initial centroids).
Assign each point to the centroid with which it has the highest cosine similarity.
Recompute each centroid by summing all vectors in the cluster and normalizing this sum to unit length.
Repeat until convergence or until changes in cluster assignments become negligible.
Below is a simplified Python example:
import numpy as np
def spherical_kmeans(X, k, max_iter=100, tol=1e-4):
# X is assumed to be an (n_samples, n_features) array.
# Normalize all vectors in X to have unit length.
X_norm = X / np.linalg.norm(X, axis=1, keepdims=True)
# Randomly pick initial centroids among the data points.
n_samples = X_norm.shape[0]
idx = np.random.choice(n_samples, k, replace=False)
centroids = X_norm[idx, :]
for _ in range(max_iter):
# Compute cosine similarity between X_norm and centroids.
# cos_sim shape: (n_samples, k)
cos_sim = np.dot(X_norm, centroids.T)
# Assign cluster labels based on maximum cosine similarity
labels = np.argmax(cos_sim, axis=1)
new_centroids = np.zeros_like(centroids)
# Compute new centroids
for cluster_idx in range(k):
# Gather all points assigned to this cluster
cluster_points = X_norm[labels == cluster_idx]
if len(cluster_points) > 0:
centroid_vector = np.sum(cluster_points, axis=0)
# Normalize
new_centroids[cluster_idx] = centroid_vector / np.linalg.norm(centroid_vector)
else:
# In case of an empty cluster, re-initialize randomly
random_idx = np.random.choice(n_samples)
new_centroids[cluster_idx] = X_norm[random_idx]
# Check convergence
shift = np.linalg.norm(centroids - new_centroids)
centroids = new_centroids
if shift < tol:
break
return labels, centroids
This snippet highlights the main differences from conventional k-Means: the use of cosine similarity for assignment and normalization of centroids.
Possible Pitfalls and Special Considerations
Clustering high-dimensional data can be challenging because distances (or similarities) tend to concentrate and the data can be very sparse. Although Spherical k-Means addresses some of these issues by focusing on direction, initialization can still affect the clustering outcome significantly. Also, if the data has outliers or extremely high frequency terms, normalizing all vectors might not fully eliminate the influence of those high-frequency terms, so additional preprocessing steps like TF-IDF transformation or stop-word removal are typically applied.
Follow-up Questions
Why does cosine similarity matter more than Euclidean distance in text data?
Cosine similarity typically captures the overlap in features (words) between documents without getting influenced by differences in length. Text vectors are often sparse and vary significantly in magnitude, so measuring similarity based on direction (angle between vectors) is often a more consistent representation of document-relatedness compared to raw Euclidean distance.
Could we apply Spherical k-Means to other domains besides text?
Yes. Any domain where normalized direction plays a more crucial role than magnitude can benefit from Spherical k-Means. For instance, certain image feature representations, audio signals, or embeddings in NLP tasks could also be clustered effectively with direction-based similarity. The algorithm is not limited to text, but text is one of the most common use cases.
How do we handle convergence and initialization issues?
Spherical k-Means, like standard k-Means, can converge to a local optimum, so initializing centroids in different ways and running multiple times is common practice. Methods like k-means++ (adapted for spherical spaces) can help produce better initial centroids. Checking inertia or the total cosine similarity can be used to track convergence.
Are there any computational complexity concerns with high-dimensional data?
Yes. The computational complexity of each iteration is roughly O(n_samples * k * n_features). In high-dimensional settings, this can be expensive. Techniques such as approximate nearest neighbor searches, dimensionality reduction (e.g., PCA), or specialized data structures can help mitigate these issues, depending on the size of the dataset and the available compute resources.
How do outliers affect the clustering?
If outliers have very different term distributions compared to most of the data, they might still end up forming their own cluster or distorting the centroid calculation, even after normalization. One strategy is to remove or down-weight these outliers before clustering, or employ robust clustering variants that reduce the impact of extreme points.
Why do we normalize the centroids after each update?
Normalizing the centroids forces them to lie on the unit hypersphere, making the algorithm's distance or similarity metric consistent with the data vectors. This ensures that the cluster center represents a direction rather than a point in raw Euclidean space, aligning with the fundamental idea of Spherical k-Means.
In a real-world text-processing pipeline, how would I integrate Spherical k-Means?
You would typically:
Preprocess your text documents with tokenization, stop-word removal, and TF-IDF transformation.
Normalize each TF-IDF vector to unit length.
Perform Spherical k-Means on the normalized vectors.
Use the resulting clusters to identify document groupings or semantic themes.
This approach is common in recommendation systems, search engines, topic clustering, and many other NLP-related tasks.