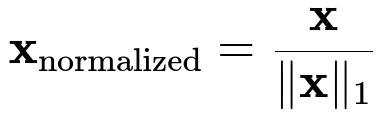ML Interview Q Series: What is the l₁ Normalization of a data?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

l₁ normalization (often called L1 normalization) is the process of scaling a data vector so that the sum of the absolute values of its components equals 1. This method is frequently used in various machine learning and data processing tasks to ensure each data sample has a consistent scale when training models, especially those that rely heavily on feature magnitude comparisons.

When dealing with a vector x in an n-dimensional space, the l₁ norm is defined as the sum of the absolute values of all its components. Mathematically, it can be represented as:

Here, x is a vector [x_1, x_2, ..., x_n]. Each x_i is the ith component of x, and n is the total number of components.

Once we compute the l₁ norm of the vector x, we obtain the l₁-normalized vector x_normalized by dividing each component of x by this norm:

In other words, the ith component of the normalized vector is x_i / (sum of absolute values of all components). This ensures that the resulting vector has a total absolute sum of 1. For example, if x is [2, -1, 3], the l₁ norm is |2| + |-1| + |3| = 6. Dividing each component by 6 yields the normalized vector [2/6, -1/6, 3/6] = [0.333..., -0.166..., 0.5], whose absolute values sum to 1.

A key characteristic of l₁ normalization is that it preserves the sparsity of a vector. If the original vector had many zero elements, they remain zero after normalization because dividing 0 by a constant is still 0. This property can be especially useful in scenarios involving high-dimensional but sparse data, as it maintains the sparsity pattern.

In practical applications, using l₁ normalization is beneficial in certain models where the sum of absolute feature contributions is meaningful. For example, in text processing with term frequency features, scaling by the l₁ norm ensures that each document’s terms sum to 1, making documents more directly comparable in terms of their relative term usage rather than raw counts.

Implementation Example in Python

import numpy as np

def l1_normalize(vector):
    norm_1 = np.sum(np.abs(vector))
    if norm_1 == 0:
        # If the vector is all zeros, return it as is or handle appropriately
        return vector
    return vector / norm_1

# Example usage:
data = np.array([2.0, -1.0, 3.0])
normalized_data = l1_normalize(data)
print("Original:", data)
print("L1 Normalized:", normalized_data)

This simple Python function computes the sum of absolute values of the elements in the vector. If that sum is zero (indicating that every element is zero), we return the original vector to avoid division by zero. Otherwise, we divide by this sum to produce the l₁-normalized version.

What Are The Advantages Of Using l₁ Normalization?

One of the major advantages is that it can make different vectors or data points directly comparable on the same scale, regardless of their original magnitude. This comparability can be helpful in tasks like feature similarity measurements or clustering, where data points’ relative proportions matter more than their absolute values. Another advantage is that it preserves or even encourages sparsity if the data is originally sparse.

How Does l₁ Normalization Compare To l₂ Normalization?

Whereas l₁ normalization scales the vector so that the sum of absolute values is 1, l₂ normalization scales the vector so that the Euclidean length (square root of sum of squares) is 1. l₂ normalization often emphasizes large components more strongly and is more sensitive to outliers, while l₁ normalization treats outliers with less emphasis. The choice between l₁ and l₂ often depends on the nature of the dataset and the downstream model’s requirements.

When Should We Not Use l₁ Normalization?

One important caveat is that if the original data vector is all zeros, or is extremely close to zero in all dimensions, normalization can become undefined or lead to numerical instability. Additionally, if the importance of absolute value sums is not meaningful in the problem domain, l₁ normalization might not be appropriate. In some cases, features may be more suitably normalized by their range (min-max scaling) or standardized to have zero mean and unit variance.

Follow-up Questions

How Does l₁ Normalization Affect Distance-Based Methods?

l₁ normalization can significantly impact distance-based methods such as K-Nearest Neighbors or clustering algorithms that rely on metrics like Euclidean distance or Manhattan distance. Because each vector’s absolute sum is forced to be 1, distances become more focused on the distribution of components rather than their magnitude. This makes sense in contexts where the shape of the vector matters more than its overall scale, such as when analyzing document term distributions in natural language processing.

When using Manhattan distance (sum of absolute differences), normalizing by the l₁ norm essentially fixes each data point on the simplex of all possible vectors whose sum of absolute values is 1. Hence, differences become more about the relative weighting of features instead of absolute magnitudes.

What Happens If The Vector Contains Negative Values?

l₁ normalization in the presence of negative values still follows the same principle. The sum of the absolute values ignores the sign of each component. Negative components will remain negative after normalization, but their absolute values contribute to the denominator in the same way positive values do. For instance, if a vector has components [3, -3], its l₁ norm is 3 + 3 = 6. After normalization, it becomes [0.5, -0.5], which still sums to zero numerically but has an absolute sum of 1.

Is There A Relationship Between l₁ Normalization And Regularization?

Yes, there is a conceptual relationship between l₁ normalization and l₁ regularization, though they serve different purposes. l₁ regularization (also known as Lasso in regression contexts) penalizes the sum of absolute coefficients in a model during training. This penalty often pushes some coefficients to exactly zero, leading to sparse solutions. While l₁ normalization simply rescales a vector, l₁ regularization modifies an optimization objective. Both place an emphasis on the absolute value function but are used at different stages of data processing or model fitting.

How Do We Handle Zero Vectors In Practice?

A zero vector, or any vector whose components are all zero, cannot be normalized by its l₁ norm because the denominator would be zero. In practice, a common approach is to leave such vectors as they are (still zero after an attempted normalization), or to treat them as missing data. The best approach depends on the application. For instance, if all-zero vectors carry no information, a model may safely ignore them or treat them as outliers.

Are There Specific Use Cases Where l₁ Normalization Is Preferable Over Other Normalizations?

l₁ normalization is typically chosen when preserving sparsity is crucial or when relative proportions of the components must be maintained. Text mining, where documents are represented by term frequencies, is a classic example. Another use case is computing probabilities of discrete events in certain modeling contexts, because normalizing by the l₁ norm can directly transform raw counts into probability distributions if all counts are nonnegative.

By understanding these nuances, you can decide if l₁ normalization is the right approach for your problem, or if other normalization or scaling techniques might be more suitable.

Below are additional follow-up questions

How Does l₁ Normalization Affect Feature Engineering?

One subtlety arises when you apply l₁ normalization in conjunction with feature engineering steps such as polynomial expansions or domain-specific transformations. Sometimes, after expanding the feature set (for example, adding interaction terms or polynomial terms), you might have features that vary drastically in magnitude. If you apply l₁ normalization afterward, all features—including the newly created ones—will be rescaled based on the absolute sum of the entire expanded vector. This can reduce the relative importance of the original features or overshadow the new features if one set dominates the sum of absolute values.

A potential pitfall is that polynomial or interaction features might be heavily influenced by the original large-magnitude features, and normalization could end up assigning disproportionate focus to smaller-magnitude features. You might unintentionally skew the model if you do not carefully analyze how normalization interacts with newly created features. It is essential to check whether the relative importance (as signaled by magnitude) should be retained or whether you genuinely want everything to have equal footing in terms of absolute contribution.

Can l₁ Normalization Exacerbate Data Imbalance Issues?

l₁ normalization can sometimes magnify issues related to class or label imbalance. For instance, if you are working with classification data that are heavily skewed—where one class heavily dominates the dataset—some features might already be near zero for minority classes. After normalizing, those near-zero values might become even less distinctive when viewed in a multi-dimensional space, making minority class data points harder to differentiate from one another or from majority class data points.

Moreover, if certain features are consistently zero in minority class samples but non-zero in majority class samples, normalization could lead to a scenario where the minority class vectors appear more uniform and less separable. It might become more challenging to detect unique signals in the minority class. A potential way to mitigate this is to combine normalization with other resampling techniques such as SMOTE or class-weighted training, ensuring that normalization does not inadvertently wash out crucial differences.

How Does l₁ Normalization Interact With Sparse Data Beyond Preserving Sparsity?

While it is true that l₁ normalization maintains zeros as zeros, there are corner cases when dealing with extremely high-dimensional sparse data—like high-dimensional text corpora or one-hot encoded categorical variables—where many features are zero for each sample. If a vector has a large number of zero entries and just a few non-zero entries, those few non-zero entries might get scaled down significantly if they are large in absolute value. This can create a scenario where most normalized vectors start looking very similar if the distribution of non-zero entries is somewhat uniform across samples.

Another subtle effect arises if the non-zero entries tend to cluster around certain features for specific data segments. After normalization, those segments might become more homogeneous, reducing the discriminative power of certain features. As a result, even though zeros remain zeros, you should carefully check if the normalized vectors are losing some of the nuance that was initially present in the magnitude differences of the non-zero entries.

What Are The Challenges Of Using l₁ Normalization In Online Learning Settings?

In online learning or streaming data scenarios where samples arrive incrementally, you may need to update feature representations in real time. With l₁ normalization, you must compute the sum of absolute values of features on the fly for each newly observed data point. If the dimensionality is very high, or if you are receiving data at a rapid rate, this computation might become costly. Additionally, if you are maintaining a model that updates with each new sample, applying l₁ normalization on the streaming data can introduce latency, especially if you need to store and normalize large sparse vectors.

Another challenge is how to handle data points that are partially observed. For example, if some features arrive with a delay, you might initially have incomplete information to calculate an accurate l₁ norm. This can lead to either partial normalization or deferred normalization until all features arrive, which can complicate your pipeline or your real-time predictions.

Can l₁ Normalization Mask Outlier Detection?

If your pipeline includes outlier detection, you should be aware that l₁ normalization might transform the scale in such a way that outliers no longer appear extreme in magnitude. Outlier detection methods often rely on distance metrics or unusual magnitude in certain features. By forcing the absolute sum of the features to 1, an outlier that had a few disproportionately large feature values may no longer stand out as much. It becomes comparable in scale to all other data points, potentially making outlier detection less effective.

In real-world scenarios, you might want to detect outliers before applying normalization, or you might use a separate method that is invariant or only partially affected by feature scaling. One approach is to do outlier detection in the raw feature space first and then apply normalization, ensuring that you do not lose the original scale-based signals that help identify unusual data points.

What Is The Role Of l₁ Normalization In Distance Metric Learning?

In distance metric learning, the choice of normalization can significantly affect how distances are measured. l₁ normalization places every data sample on a simplex, meaning the sum of their absolute values is constrained to 1. This can simplify or complicate distance metric learning tasks depending on the specific loss function used. For example, if you are using Manhattan distance (sum of absolute differences), normalizing by the l₁ norm makes each data point lie in a space where the sum of absolute components is uniform. Distance computations might become more sensitive to relative differences in component proportions.

However, if your task requires capturing the overall magnitude differences between data samples, l₁ normalization can actually remove that signal entirely. Hence, if your distance metric or its learned parameters rely on overall scale disparities, l₁ normalization might diminish the model’s ability to capture them. You need to carefully assess whether your final metric is meant to capture proportion-based similarity (where l₁ normalization is useful) or magnitude-based similarity (where it is not).

What Happens When We Combine l₁ Normalization With Nonlinear Kernels In SVMs?

In Support Vector Machines that use nonlinear kernels (e.g., RBF kernels), the scale of the input space can heavily influence the kernel values. l₁ normalization ensures each data point has an absolute sum of 1, which might or might not align with the assumptions behind the chosen kernel. For instance, if you were using an RBF kernel that is sensitive to Euclidean distances, forcing the input vectors to all have unit l₁ norm might cause distances between points to be primarily driven by which features are non-zero rather than how large they are in magnitude.

A potential pitfall is that hyperparameter tuning of the kernel parameters (like the gamma parameter in an RBF kernel) can become trickier, because the distribution of distances in the transformed feature space is altered by normalization. You might need a more careful grid search or cross-validation procedure to identify suitable kernel hyperparameters. Also, if the kernel is extremely sensitive to small differences, the uniform l₁ norm might inadvertently flatten or sharpen the kernel’s notion of distance, depending on how the features are distributed.

Does l₁ Normalization Impact Gradient-Based Optimization?

l₁ normalization can have implications for gradient-based optimization methods when you are updating parameters of a model that takes normalized inputs (e.g., a neural network). If the inputs to your model are always on the simplex, the gradient signals that flow back into earlier layers may differ substantially from a scenario where inputs are not normalized. This could accelerate convergence in some cases, especially where scale-based differences do not matter. However, it can also hamper optimization if the network architecture or loss function implicitly relies on scale to separate classes or to embed data meaningfully.

An edge case is when your input features occasionally become zero vectors, either by design or by some data corruption. If your training procedure does not handle those zero vectors gracefully, you could see abrupt changes in the gradients or NaN values. For example, if your code attempts to normalize a zero vector by dividing by zero, you might inadvertently insert undefined values into the training pipeline. Proper error handling or a fallback strategy for zero vectors is critical.

How Might l₁ Normalization Influence Ranking Metrics?

In tasks involving ranking (such as information retrieval), the scale of feature values often impacts the ranking score your model produces. If you apply l₁ normalization on each item or document separately, the sum of absolute feature values for each item becomes 1, which might make items that naturally had larger magnitudes lose some of their distinctiveness. This can flatten the range of scores that a ranker might assign, leading to potential ties or near-ties.

For instance, consider a recommendation system that uses item embeddings as features. If the magnitude of an embedding signaled a strong presence or frequency of certain characteristics, l₁ normalization would remove that direct magnitude signal and only retain proportional differences among feature components. Some ranking metrics, such as normalized discounted cumulative gain (NDCG), are sensitive to how items are relatively scored. You might find that the ranking output changes if items no longer have a wide spread of magnitudes.

If your ranking task relies heavily on the absolute intensities of features (like the frequency of user interactions), you should weigh carefully whether l₁ normalization aligns with the nature of your ranking objectives.