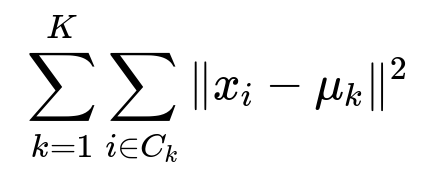ML Interview Q Series: What specific cost function does k-Means attempt to minimize, and how is it formulated?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

k-Means is an unsupervised clustering algorithm that partitions data into K clusters. Each cluster is represented by a centroid, which is the mean position of all points assigned to that cluster. The algorithm aims to minimize the overall dispersion of the data points relative to these centroids. This dispersion is usually measured via the sum of squared distances between each point and the centroid of its assigned cluster.

In this expression:

• K is the number of clusters.

• C_k is the set of data point indices assigned to cluster k.

• x_i is the i-th data point in a d-dimensional feature space.

• mu_k is the centroid (mean) of cluster k.

• The notation \| x_i - \mu_k \|^2 represents the squared Euclidean distance (sum of squared differences across the feature dimensions) between x_i and its assigned centroid mu_k.

Minimizing the above sum of squared distances is the key objective. The algorithm alternates between assigning each data point to its closest centroid (assignment step) and then re-computing the centroid of each cluster (update step) based on the points assigned in the previous step. This iterative procedure continues until convergence, typically meaning the assignments no longer change or the change is below a certain threshold. The solution achieved is a local minimum of the stated objective function.

Because the objective function is not convex with respect to both the assignments and the centroids simultaneously, k-Means can converge to local minima. To mitigate this, practitioners often run the algorithm multiple times with different initializations and choose the result that yields the best (lowest) objective value.

Key Insights and Practical Considerations

One of the motivations for using the squared Euclidean distance in k-Means is that the mean minimizes the squared error to points in a cluster. If a different distance metric (for example, Manhattan distance) is used, the optimal representative of each cluster is the median instead of the mean, leading to variations of k-Means such as k-Medians or k-Medoids.

Scaling of data can significantly affect the objective value because the sum of squared distances will emphasize dimensions with larger magnitude more heavily. Preprocessing steps like feature scaling (standardization or normalization) are commonly used to balance the influence of each dimension.

Typical stopping criteria for k-Means are:

• No change in cluster assignments from one iteration to the next.

• Centroids movement below a certain small threshold.

• A set maximum number of iterations has been reached.

A practical implementation detail is to carefully initialize the centroids to avoid poor local minima. A widely used method for initialization is k-means++ (available in many standard ML libraries) which selects initial centroids in a way that attempts to spread them out in feature space.

Here is a simple Python code snippet illustrating k-Means implementation with scikit-learn:

from sklearn.cluster import KMeans
import numpy as np

# Example data
X = np.array([
    [1.0, 2.0],
    [1.5, 1.8],
    [5.0, 8.0],
    [8.0, 8.0],
    [1.0, 0.6],
    [9.0, 11.0]
])

# Choose the number of clusters
k = 2

# Initialize k-Means model
kmeans = KMeans(n_clusters=k, init='k-means++', max_iter=300, random_state=42)

# Fit model to data
kmeans.fit(X)

# Labels of each point's cluster
labels = kmeans.labels_

# Coordinates of cluster centroids
centroids = kmeans.cluster_centers_

print("Cluster labels:", labels)
print("Centroids:\n", centroids)

Why Does k-Means Use the Mean as the Centroid?

Once a set of points is assigned to a cluster, the centroid that minimizes the sum of squared distances is the mean of those points. This can be verified by taking partial derivatives of the objective with respect to the centroid and setting them to zero, leading to the mean vector solution. Using a mean makes the mathematics particularly simple during the update step and speeds up convergence.

Follow-up Questions

How Does k-Means Handle Different Feature Scales?

k-Means can be sensitive to the range of features because of its reliance on squared Euclidean distance. Features with large ranges can dominate the distance calculation, causing clusters to be formed in a way that ignores the impact of other features. A common approach is standardizing or normalizing each feature so that each dimension contributes more equitably to the distance computation.

Why Does k-Means Require a Predetermined Number of Clusters (K)?

k-Means needs the number of clusters K as a hyperparameter. The algorithm will find exactly K centroids, but if you choose K incorrectly (either too small or too large), you might underfit or overfit the data’s intrinsic cluster structure. Techniques like the Elbow Method or the Silhouette Score are often used to guide the selection of K.

What Happens if k-Means Becomes Trapped in a Local Minimum?

Because the objective function is non-convex with respect to both the centroids and the assignments, the algorithm can settle in a configuration that is not globally optimal. To reduce the chance of ending up in a poor local minimum, multiple runs with different random initializations are usually performed (the best clustering result is then chosen based on the lowest objective value). The k-means++ initialization is also popular for improving the quality of the initial centroids.

Could We Use Other Distance Metrics in k-Means?

When substituting the Euclidean distance with an L1 distance (Manhattan distance), the optimal centroid becomes the median instead of the mean. Variants like k-Medians or k-Medoids (which use actual data points as cluster centers) are used in those contexts. The choice of distance metric depends on the distribution and nature of your data.

Is k-Means Sensitive to Outliers?

k-Means is sensitive to outliers because the centroid is computed using a mean, which can be pulled significantly by extreme values. If the data contains many outliers or extreme values, the clustering results might not reflect the main “bulk” structure. In such scenarios, methods like k-Medoids can be more robust because they choose a representative data point as the cluster “center,” making them less sensitive to outliers.

Can k-Means Handle Non-Convex Clusters?

k-Means implicitly assumes clusters have a roughly spherical shape in the feature space (because it is designed to minimize squared Euclidean distances around a centroid). Consequently, it struggles with data that forms complex or elongated shapes. Other clustering methods, such as DBSCAN or spectral clustering, may be more suitable for complex cluster geometry.

How to Incorporate Categorical Features in k-Means?

k-Means is generally not well suited for purely categorical data because the mean of categorical attributes does not have an obvious interpretation. One workaround is transforming categorical variables into numerical representations (for example, via one-hot encoding), but this can increase dimensionality and still might not capture the correct notion of distance between categories. Algorithms specifically designed for mixed or categorical data (like k-Modes, k-Prototypes) are often used.

All these nuances reflect why, despite its simplicity, k-Means still requires a thorough understanding of its objective function, initialization strategies, and data preprocessing in real-world applications.