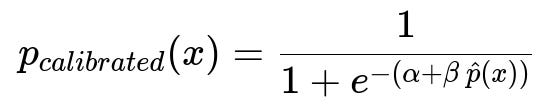ML Interview Q Series: What strategies would you use to adjust a classifier’s output probabilities so that they align more precisely with the actual likelihood of the classes?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Probability calibration is the process by which we transform a classifier's raw score or predicted probability into a better-aligned estimate of how likely each class truly is. The ultimate goal is for the model to produce probabilities that match the real frequency of occurrence. For example, among all predictions labeled with probability 0.7, we hope that roughly 70% of those cases actually belong to the positive class.
Calibration becomes particularly important when predictions feed into downstream decisions (such as medical diagnoses or credit risk evaluation) where the exact probability affects critical thresholds and cost-benefit analyses. Well-calibrated probabilities help ensure that domain experts and automated pipelines can interpret the model’s outputs more confidently.
One common practice is to fit a small secondary model on top of the original classifier's outputs. A straightforward approach is Platt scaling, which uses a logistic (sigmoid) transformation of the raw model outputs, possibly turning a non-logistic classifier into well-calibrated probabilities. Another technique is isotonic regression, a non-parametric method that can flexibly capture the relationship between raw outputs and true probabilities without forcing a single parametric form.
A typical logistic-based calibration might look like this when calibrating raw scores hat{p}(x) from the original classifier:
Here, p_calibrated(x) is the calibrated probability; alpha and beta are parameters (scalar constants) learned on a separate validation set; and hat{p}(x) is the raw model score for input x. Usually, hat{p}(x) might be a log-odds output (or some continuous score) from the original classifier. The calibration step solves for alpha and beta by fitting a logistic regression that predicts the actual outcomes from the raw scores.
Fitting these parameters requires a held-out validation set or cross-validation process. The model that produced hat{p}(x) remains untouched; only alpha and beta are learned so that p_calibrated(x) better matches observed frequencies. Isotonic regression works similarly but uses a piecewise-constant function to map raw scores to probabilities. This is more flexible than a single logistic transformation but can be prone to overfitting if data is sparse.
To evaluate if a model is well-calibrated, practitioners often rely on reliability diagrams or calibration curves. These visuals group predictions by probability bins (e.g., 0.0–0.1, 0.1–0.2, etc.) and compare the average predicted probability within each bin to the actual fraction of positives observed. A perfectly calibrated model’s points in the reliability diagram fall on a 45-degree line. Numerical measures like the Brier score, log loss, or the Expected Calibration Error can further help quantify calibration quality.
Below is a simplified Python code snippet illustrating how one might perform calibration using scikit-learn. It shows an example of training a classifier, predicting probabilities, and then applying a calibration method such as Platt scaling (known in scikit-learn as “sigmoid”) or isotonic regression:
import numpy as np
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.calibration import CalibratedClassifierCV
from sklearn.model_selection import train_test_split
from sklearn.metrics import brier_score_loss
# Generate synthetic data
X, y = make_classification(n_samples=10000, n_features=20, n_informative=10,
random_state=42)
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2,
random_state=42)
# Train a base classifier
base_clf = LogisticRegression()
base_clf.fit(X_train, y_train)
# Obtain raw (uncalibrated) predictions
y_probs_uncalibrated = base_clf.predict_proba(X_val)[:, 1]
# Calibrate the classifier using Platt scaling
calibrated_clf_sigmoid = CalibratedClassifierCV(base_clf, cv='prefit',
method='sigmoid')
calibrated_clf_sigmoid.fit(X_val, y_val)
y_probs_sigmoid = calibrated_clf_sigmoid.predict_proba(X_val)[:, 1]
# Calibrate the classifier using Isotonic Regression
calibrated_clf_isotonic = CalibratedClassifierCV(base_clf, cv='prefit',
method='isotonic')
calibrated_clf_isotonic.fit(X_val, y_val)
y_probs_isotonic = calibrated_clf_isotonic.predict_proba(X_val)[:, 1]
# Compare calibration quality using Brier score (lower is better)
brier_uncalibrated = brier_score_loss(y_val, y_probs_uncalibrated)
brier_sigmoid = brier_score_loss(y_val, y_probs_sigmoid)
brier_isotonic = brier_score_loss(y_val, y_probs_isotonic)
print("Brier uncalibrated: ", brier_uncalibrated)
print("Brier Sigmoid (Platt) calibrated: ", brier_sigmoid)
print("Brier Isotonic calibrated: ", brier_isotonic)
By comparing these different Brier scores, one can see if either Platt scaling or isotonic regression significantly improves calibration compared to the original uncalibrated classifier. The approach generalizes to any classifier’s probability scores (random forests, gradient boosting, neural networks, etc.), as long as a separate calibration dataset is available.
How Would You Evaluate Calibration in Practice?
Evaluating calibration commonly involves two approaches: graphical and numerical. A reliability diagram (or calibration plot) provides a visual tool. You sort predictions into bins according to their predicted probability. For each bin, you calculate the actual fraction of positives. Plotting these fractions (y-axis) against the average predicted probabilities (x-axis) reveals if the model is overconfident (points lie above the diagonal) or underconfident (points lie below the diagonal).
From a numerical standpoint, metrics like the Brier score (the mean squared error between predicted probabilities and actual outcomes) or the log loss provide a combined view of both calibration and discrimination. Some metrics such as the Expected Calibration Error explicitly measure deviations from perfect calibration, focusing solely on alignment of predicted probabilities with true frequencies.
Why Might Platt Scaling Sometimes Fail?
Platt scaling imposes a specific parametric form (logistic) on the relationship between raw scores and calibrated probabilities. If the underlying relationship is more complex, or if the raw scores are not linearly related to the log-odds of the class probabilities, a single sigmoidal curve may not be flexible enough. This limitation can cause underfitting of the calibration function, especially if the base model’s scores do not exhibit a near-logistic shape.
Data scarcity and class imbalance can also make Platt scaling less robust. If there are not enough validation samples, the fitted logistic parameters alpha and beta might not generalize. In such cases, isotonic regression can sometimes provide a more flexible (though also more data-hungry) alternative.
How Do Isotonic Regression and Platt Scaling Compare?
Both methods attempt to produce well-calibrated probabilities, but they differ in their assumptions and flexibility. Platt scaling uses a logistic curve, which enforces a monotonic parametric shape. Isotonic regression, by contrast, is a non-parametric, piecewise-constant method that guarantees a non-decreasing mapping from raw scores to probabilities. It can produce stepwise functions that better capture intricate patterns in the score-to-probability relationship if enough data is available.
However, isotonic regression can overfit when data points are limited, potentially creating abrupt changes. Platt scaling is typically more robust with fewer validation samples, but it may not capture more nuanced relationships. In practice, data availability and the shape of the raw score distribution guide the choice.
What Happens If We Use the Same Data for Model Training and Calibration?
A common mistake is to reuse the same training set or the exact same samples for both fitting the model and calibrating the probabilities. This leads to overly optimistic results because the calibration method memorizes or partially compensates for the model’s idiosyncrasies on that training set. The correct practice is to either split off a separate held-out set or use a cross-validation approach to ensure calibration parameters are learned on data not seen by the original model training process. This helps maintain proper generalization and avoids overfitting the calibration function.
How Would Calibration Work with Multi-Class Problems?
Calibration extends naturally to multi-class settings, although it becomes more complex. One strategy is to build separate one-vs-rest calibrators for each class. Another approach is to use Dirichlet calibration, which generalizes Platt scaling for multiple classes by modeling a set of parameters that transform the raw score vector into a properly calibrated probability distribution. However, these approaches usually require more data and a careful approach to ensure robust calibration across multiple classes.
Could You Combine Calibration with Model Training in One Step?
In principle, some methods integrate calibration directly into the model training loss function, effectively teaching the model to produce calibrated probabilities from the start. Neural networks often do something similar by optimizing cross-entropy, which can encourage well-formed probabilities. Still, networks frequently produce overconfident outputs, suggesting that post-hoc calibration is often necessary. Joint training with calibration constraints can be more complex to implement and tune, so many practical pipelines prefer to keep the calibration step separate.
What if the Model Outputs are Already Calibrated?
Some models, like logistic regression or well-regularized neural networks with certain temperature scaling techniques, can yield fairly well-calibrated outputs from the start. However, it is always wise to validate calibration explicitly rather than assume it. Real-world distributions can change, or the model might not be as well-calibrated as theory might suggest. Monitoring a calibration plot or Brier score on a validation set is still recommended to confirm that the output probabilities align with actual frequencies.
Below are additional follow-up questions
How Does Domain Shift Affect Probability Calibration?
When the data distribution used during calibration differs significantly from the data encountered during inference, the calibration map may not hold. Domain shift arises in many real-world applications—for instance, a model trained on historical financial data may not remain valid during an economic crisis. A key pitfall is that your Platt scaling or isotonic regression could be tuned to a distribution that no longer applies, causing the calibrated probabilities to become unreliable.
Adapting to domain shift often involves periodically recalibrating the model on data representative of the new domain. One approach is continuous calibration, where you routinely collect fresh samples from the evolving data distribution and update the calibration parameters. Alternatively, if you suspect only minor shifts, domain adaptation methods (like distribution matching) can help transform the new data to resemble the calibration dataset, but this can be complicated. In practice, monitoring calibration metrics (e.g., reliability diagrams) on newly observed data is critical to catching domain shift.
Can Temperature Scaling Be Used Instead of Platt Scaling or Isotonic Regression?
Temperature scaling is particularly common in deep learning, where models tend to output overconfident probabilities. The idea is to learn a single temperature parameter T that scales the logit layer before the final softmax for classification. If z is the model’s logit output for a given class, you replace it with z/T and then apply softmax. This method is simpler than Platt scaling because it only requires learning one scalar parameter T instead of two (alpha and beta) or a more complex piecewise mapping.
The main benefit is computational simplicity: temperature scaling rarely overfits because there is only one parameter. However, it assumes that all classes and logits need a uniform temperature adjustment. If your model’s miscalibration is more class- or region-specific, temperature scaling could be too rigid. Unlike isotonic regression, it cannot reshape the probability curve in a highly flexible way. Nonetheless, it can be a good first attempt when calibrating neural networks.
What If My Classifier Only Produces Hard Labels or Ranks Instead of Probabilities?
Some models, such as certain tree-based ensembles in their default mode, produce only predicted classes (0 or 1) or a rank ordering of instances rather than continuous probability estimates. Calibration presupposes you have some type of raw score or probability output to map to a better probability. If your model does not provide these, you have a few options:
Modify or reconfigure the model to produce probability estimates or scores. For random forests, for example, you can enable out-of-bag probability estimation. For SVMs, you could enable probability estimates via Platt scaling built into certain libraries.
Use rank-based calibration methods. Some techniques can convert a ranking into a probability distribution by correlating rank percentiles with empirical class frequencies. But these methods can be less straightforward and require careful binning or isotonic-like transformations.
A pitfall is to force a calibration method on discrete 0/1 outputs. You cannot calibrate a discrete label further; you need an intermediate continuous or at least ordinal score.
Can Overcalibration Degrade the Model’s Discriminative Power?
Overcalibration can occur when the fitting of calibration parameters (like the piecewise mapping in isotonic regression) starts to memorize the noise or peculiarities of the small calibration set. While your reliability diagram may appear nearly perfect on that set, the model might become less generalizable and degrade in terms of discrimination (the ability to rank positive vs. negative instances correctly). A classical symptom is that your calibration performance looks great in-sample but collapses out-of-sample.
The best safeguard against this is to hold out or cross-validate the calibration step—never calibrate on the same data used to train the base model. Monitoring both calibration metrics (Brier score, reliability diagram) and discrimination metrics (AUC, precision-recall) on a separate test set helps verify that you have not impaired the model’s ability to separate classes while improving calibration.
How Do You Handle Highly Imbalanced Datasets During Calibration?
Imbalanced datasets, where one class is much rarer than the other, pose challenges for calibration. Even if the overall accuracy or AUC is high, the model may rarely assign probabilities near 1.0 for the minority class, causing biased calibration curves. A potential pitfall is that standard calibration methods might underrepresent the minority class distribution, leading to systematically skewed calibrated probabilities.
One approach is to perform stratified sampling or weighting so that the calibration procedure sees enough minority examples. Additionally, you can apply class-weighting or oversampling in the calibration set, though you must be careful that such manipulations do not distort real-world frequency. In extremely imbalanced scenarios, the model might produce probabilities that are indistinguishable from near-zero for the minority class; isotonic regression could create large step changes that overfit. Evaluating calibration specifically within each class—sometimes called classwise calibration—can be a more informative approach.
What if the Predicted Probabilities Are Always Extremely Confident (Near 0 or 1)?
Some classifiers—especially deep neural networks—tend to push probabilities toward the extremes of 0 or 1. This can cause calibration difficulties because standard methods like Platt scaling assume a smoother score distribution. If the raw outputs saturate, the calibration model may only see a narrow band of possible scores, making it harder to learn a reliable mapping. Platt scaling might squash everything between, say, 0.99 and 1.0 into nearly the same region.
One solution is to add a regularization term or technique that encourages less extreme probabilities in the base model. Another is to use a more flexible method (e.g., isotonic regression) on a large calibration set. If data is limited and you repeatedly see outputs of 0 or 1, calibration might fail to meaningfully adjust those extreme values, leaving you with a poorly calibrated system. Monitoring calibration curves across all probability bins can help reveal if you are collapsing too many samples into the edges.
How Do We Approach Sequential Calibration in an Online Learning Scenario?
In online learning or streaming contexts, new data arrives continuously. You cannot simply train a model and a calibrator on a static dataset. Instead, you might adopt an incremental calibration strategy. When new data points come in, you update both the base model (or keep it frozen if the model is not being retrained) and the calibration mapping. This could be done with:
A rolling window approach, where older data is dropped as new data arrives, recalibrating periodically.
Online isotonic regression, which is more challenging because standard isotonic regression is not trivially incremental.
Real-time updates to temperature parameters, where small adjustments to T are made as new performance metrics are observed.
A pitfall is that the calibration model might lag behind sudden shifts in the data distribution. Additionally, it can become computationally expensive if you recalibrate too frequently. Balancing the frequency of recalibration with the drift velocity of your data stream is crucial.
Does Calibration Necessarily Improve the Expected Value of the Decision?
Calibration ensures that predicted probabilities align with observed frequencies, but it does not always guarantee better classification decisions if your sole objective is to optimize accuracy or a specific threshold-based metric. For instance, if you only care about maximizing a standard 0.5 threshold classification accuracy, a certain level of overconfidence or underconfidence may not always worsen the final accuracy. However, in many real-world settings, a well-calibrated probability is essential for risk assessment, cost-sensitive decisions, or other tasks where the precise probability matters.
A subtle edge case is when your decision boundary depends heavily on cost functions that might make a slight miscalibration beneficial for some narrow objective. But typically, for fairness and interpretability—especially in regulated industries—being well-calibrated remains a priority.
How Do You Calibrate Stochastic Models That Vary at Inference Time?
Certain ensemble methods or Bayesian neural networks produce variable outputs due to sampling from a posterior distribution at inference. Calibration can become more complicated if the predicted probability itself is a random variable. One strategy is to average predictions from multiple draws to get a mean probability, then calibrate that mean. Alternatively, some practitioners apply calibration to each draw’s predictions, though this is more complex.
A pitfall is ignoring the variance and focusing only on the mean predicted probability. In some applications, the uncertainty (variance) around the probability is crucial, and naive calibration might overlook it. Proper Bayesian calibration approaches can incorporate the posterior predictive distribution instead of a single point estimate. However, implementing these methods can be more involved and requires specialized libraries and theoretical understanding.
Can Post-Hoc Calibration Techniques Fix Poor Feature Representations?
Post-hoc calibration only adjusts the output layer or final predicted probabilities, not the internal representations learned by the model. If your model’s features are deeply flawed or missing critical signal, no amount of calibration can fix the fundamental inability to separate classes well. Calibration may make the probabilities appear more aligned with observed frequencies, but the model might still fail to distinguish positive and negative instances effectively.
An important pitfall is placing too much faith in calibration to rectify an inherently underfitted or mis-specified model. The best practice is to ensure the model itself is well-trained with meaningful features, then apply calibration as a finishing step. If the base model is severely biased or lacks discrimination, further data collection or feature engineering might be more impactful than trying to calibrate a fundamentally poor predictor.