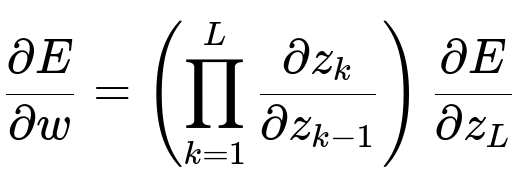ML Interview Q Series: What strategies exist to handle a cost function that yields vanishing or exploding gradients for very deep networks?

📚 Browse the full ML Interview series here.

Hint: Think about gradient clipping, residual connections, or reparameterization.

Comprehensive Explanation

Vanishing or exploding gradients are serious issues encountered in the training of very deep neural networks. These problems arise because during backpropagation, the gradient gets multiplied many times by small or large values, causing it to either shrink to near zero or blow up to very large magnitudes.

One way to see how vanishing and exploding gradients occur is by examining the repeated multiplication of partial derivatives through the chain rule. Consider a deep network with many layers. Let E be the loss function, and z_k be the output at layer k before any nonlinear activation. Backpropagation uses a chain of derivatives to compute the gradient with respect to parameters w in earlier layers. At a high level:

Here, L is the total number of layers. If the term partial(z_k)/partial(z_{k-1}) is consistently less than 1 in magnitude, the product shrinks as the number of layers increases. Conversely, if those partial derivatives are larger than 1, the product can grow very rapidly and produce exploding gradients.

Below are some commonly used strategies to mitigate these problems:

Careful Weight Initialization

Initializing weights so that the variance of the activations and gradients remains stable is critical. Techniques such as Xavier initialization (which scales weights based on the number of input and output neurons) and He initialization (which takes into account ReLU-like activations) help ensure gradients neither explode nor vanish excessively in the initial stages of training.

Gradient Clipping

Gradient clipping is a straightforward method that enforces a predefined maximum norm (or value) on the gradients. If the gradient norm exceeds a specified threshold, it is scaled down proportionally, ensuring its magnitude does not become excessively large.

In code, this can look like the following (using PyTorch as an example):

import torch

model = MyDeepModel()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)

for data, target in dataloader:
    optimizer.zero_grad()
    output = model(data)
    loss = loss_function(output, target)
    loss.backward()
    torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=2.0)
    optimizer.step()

Residual Connections

Residual (or skip) connections, popularized by ResNet architectures, directly add the input of a layer to its output. This short-circuiting helps gradients flow back more directly through earlier layers without always being multiplied by many small or large derivatives. In practice, a residual block has the form:

def residual_block(x):
    y = F.relu(conv1(x))
    y = conv2(y)
    return x + y  # Skip connection

The skip connection ensures that even if part of the gradients vanish or explode in the deeper transformations, there is still a direct path for gradient flow.

Normalization Layers

Batch Normalization, Layer Normalization, or other normalization techniques can help stabilize hidden activations and reduce internal covariate shift. These normalization steps can alleviate some of the vanishing or exploding gradient problems by keeping activations in a manageable range. For example, Batch Normalization normalizes the output of a layer across a mini-batch to have mean=0 and variance=1 (then learns an affine transform for shift and scale). This regularizes training and can help maintain stable gradient magnitudes.

Reparameterization

Reparameterization can help in some contexts (like Variational Autoencoders or certain architectures prone to large parameter updates). Instead of learning parameters directly in forms that cause large gradient magnitudes, one reparameterizes them. A classic example is the reparameterization trick in Variational Autoencoders: instead of sampling from Normal(mu, sigma), one samples from a standard Normal(0,1) and then shifts and scales by learned parameters. This approach can sometimes reduce gradient variance, though it is more commonly used to enable backpropagation through stochastic nodes. More generally, reparameterizing or transforming the parameter space can help stabilize gradients if done carefully.

Using Appropriate Activation Functions

Choosing activation functions such as ReLU or its variants (Leaky ReLU, ELU, GELU) is often more effective at mitigating the vanishing gradient problem than using saturating non-linearities like the sigmoid or tanh, especially in very deep networks.

Regularization and Smaller Learning Rates

When gradients become very large, sometimes simply lowering the learning rate can help avoid instability. Additionally, standard regularization techniques like weight decay (L2 regularization) or Dropout can limit parameter growth and help keep gradients in check.

Overall, each of these strategies addresses a different dimension of the vanishing/exploding gradient challenge. In practice, a combination—such as using residual connections, proper initialization, normalization layers, and gradient clipping—often proves most effective.

How does gradient clipping get implemented in practice?

Gradient clipping is typically done right after the gradient is computed (loss.backward() in PyTorch, for example) but before the optimizer step. Most deep learning frameworks provide utility functions to clip gradients by their value or their norm. By clipping the gradients, we ensure the maximum allowable size of the gradient is limited to a safe range. This prevents very large updates to model parameters that could otherwise cause instability or divergence during training.

Why do residual connections help avoid vanishing gradients?

Residual connections add a direct path for the gradient to flow from the output layer back to earlier layers. Without them, the gradient has to pass through each layer's transformations, which can lead to repeated multiplication by small values and result in vanishing gradients. By adding the identity mapping, we bypass part of this repeated multiplication, thereby preserving more of the original gradient signal even in very deep networks. This approach makes training deep architectures (like 50, 101, or even more layers) practical.

What is the reparameterization trick, and how does it help with gradients?

The reparameterization trick is often used in stochastic computations such as Variational Autoencoders. Instead of sampling z ~ Normal(mu, sigma), one samples epsilon ~ Normal(0, 1) and then sets z = mu + sigma * epsilon. This approach allows the gradient to flow through mu and sigma because the random sampling is isolated to epsilon, which does not depend on learnable parameters. In contexts where large updates or gradient variance are problems, reparameterizing can make the backpropagation more stable, since the direct dependence on parameters is somewhat “factored out” by the transformation. Although it is not a universal fix for vanishing or exploding gradients, it can help in architectures that rely on stochastic nodes.

Under what scenarios might gradient clipping be detrimental?

While gradient clipping helps curb exploding gradients, it can also interfere with learning by uniformly scaling down all gradients when the threshold is crossed, potentially obscuring important gradient signals. If the clipping threshold is too small, training may slow down or get stuck. Additionally, if exploding gradients were indicative of some deeper problem in the model (e.g., incorrect parameter initialization or architecture design), clipping only treats the symptom, not the underlying cause. Hence, although it can prevent catastrophic updates, it is not a substitute for a well-constructed network architecture and good hyperparameter choices.

How do normalization layers specifically address the exploding or vanishing gradient issue?

By keeping the distributions of layer activations more consistent across different mini-batches and timesteps, normalization layers reduce the variation of outputs. This means the subsequent layers receive inputs that are not overly large or small, helping to keep gradients within a more stable range. Additionally, normalization layers help reduce the sensitivity to network initialization and can speed up training convergence. This stability in intermediate activation distributions lowers the chance of repeatedly multiplying by very large or very small values, which is the root cause of exploding or vanishing gradients.

Below are additional follow-up questions

How do data preprocessing and feature scaling affect vanishing or exploding gradients?

Data preprocessing and feature scaling can significantly influence the stability of gradients in deep networks. If features vary by orders of magnitude or contain outliers, the neural network may produce disproportionately large or small activations in the early layers, propagating through the network and affecting subsequent gradient magnitudes. Standardizing data (subtracting mean and dividing by standard deviation) or applying min-max scaling helps maintain consistent input distributions, which allows backpropagated gradients to stay within more reasonable ranges.

In real-world scenarios, many datasets have skewed distributions with heavy tails. A big pitfall is that if you fail to detect these heavy tails, large values can pass into the network, causing instabilities in the forward pass and potentially exploding gradients during backpropagation. Another subtlety is that for time-series or streaming data, normalization parameters (mean, variance) may shift over time, so a static normalization might become outdated. In such cases, you might need online or rolling statistics for normalization. Skipping or inadequately performing such preprocessing can be detrimental, especially for deeper architectures.

What are some specific indicators that vanishing or exploding gradients might be happening?

One obvious indicator is when your model’s training or validation loss stops decreasing or even becomes NaN. Another sign is that the updates to parameters become extremely large or extremely small. For instance, if you track model weights across iterations and observe that they remain almost unchanged, you might suspect vanishing gradients. Conversely, if you see your model weights blow up to extremely large magnitudes or start oscillating wildly, that suggests exploding gradients.

Additional deeper diagnostics include: Monitoring gradient norms per layer: If the norm in deeper layers is consistently much smaller (in the case of vanishing) or larger (in the case of exploding) than in shallower layers, you know precisely where the problem occurs. Visualizing activation histograms: If activation outputs in certain layers saturate at the extremes of the activation function, that often points to vanishing or exploding gradient issues in those layers. One subtle pitfall is that sometimes gradients do not explode immediately but gradually become larger over multiple epochs. Therefore, tracking gradient norms over time and not just at the start of training can reveal such creeping issues.

In which specific circumstances would using saturating activation functions like sigmoid or tanh still be advisable despite the risk of vanishing gradients?

Saturating activations like sigmoid or tanh can help when you want an output that is constrained within a specific range. For instance, if you need a probability-like output (0 to 1) or if you are building an autoencoder that requires compressed representations in a bounded space, you might use these activations near the output layer.

Sigmoid or tanh units can still be used effectively in certain shallow architectures or in the gating mechanisms of recurrent networks like LSTMs or GRUs, where the gating structure compensates for some of the saturation effects. Even though these gating functions are sigmoidal, they are surrounded by other design elements (like cell states) that help preserve gradients in practice.

A real-world edge case is a system with extremely small memory or computational resources, where more advanced activation functions might not be supported or might be computationally expensive. In such a case, careful design with normalized inputs, short network depth, or specialized architectures can mitigate the vanishing gradient problem sufficiently to still use these traditional nonlinearities.

How does the choice of optimizer (e.g., SGD vs. Adam vs. RMSProp) relate to vanishing or exploding gradients?

Different optimizers handle gradient magnitudes and direction updates in distinct ways. For example, vanilla SGD uses a constant learning rate and applies gradient updates as is. If gradients explode, vanilla SGD often fails quickly unless you manually tune the learning rate or apply gradient clipping. On the other hand, Adam and RMSProp keep per-parameter running statistics of the gradients, adaptively scaling updates based on recent gradients’ variance or magnitude. This adaptive approach can sometimes mitigate the risk of exploding gradients by reducing the effective learning rate for parameters with large gradients.

A hidden pitfall is that if your data is very noisy or poorly normalized, adaptive optimizers can still end up with large updates in the early stages. Consequently, even Adam and RMSProp might require gradient clipping or other strategies in extremely deep or complex models. Another subtlety is that adaptive optimizers, while helping to manage some forms of gradient explosion, do not necessarily solve all vanishing-gradient issues, especially in very deep networks with saturating activations.

Can multi-branch architectures (e.g., Inception-like networks) exacerbate or alleviate vanishing/exploding gradients?

Multi-branch architectures can alleviate gradient problems if they incorporate skip connections or if each branch is relatively shallow. The separate branches can effectively act like parallel paths for gradient flow, helping mitigate some of the repeated multiplication. However, in complex branching structures without careful design, one branch might carry extremely large or small gradient signals that do not get averaged effectively with other branches. This leads to potential instability when combining gradients at the merging layers.

In real-world scenarios, if one of the branches is significantly deeper or uses a different activation function with different scaling properties, that branch might produce gradient magnitudes that overshadow the others. Hyperparameter tuning for each branch, such as the learning rate, weight initialization, or normalization strategy, becomes more complex. Pitfalls arise when the network is not well balanced, leading to vanishing or exploding gradients in only certain branches, making debugging much harder.

How do recurrent networks (LSTMs, GRUs) deal with vanishing or exploding gradients, and what pitfalls remain?

Recurrent architectures with gating mechanisms like LSTMs and GRUs specifically address the vanishing gradient problem by introducing a cell state or hidden state that can carry information over many timesteps. The gates (input, forget, and output) control how information flows in or out of these states, mitigating repeated multiplications by small derivatives that characterize simple RNNs.

Despite this, exploding gradients still occur in RNNs when inputs are long sequences with highly correlated features, causing partial derivatives to become very large. This is why gradient clipping is almost standard for training RNNs. Additionally, if the gating functions saturate repeatedly, vanishing gradients can resurface, particularly in poorly initialized or extremely deep recurrent architectures (like stacked LSTMs). A subtle pitfall is that if the forget gate is constantly set to near 1, the cell state might accumulate large or uninformative values over time. This can cause extremely large weight updates once the gradient is finally able to flow back through the gating function.

What role does the design of the loss function play in vanishing/exploding gradients?

Some loss functions produce higher gradient magnitudes than others. For example, a mean squared error loss can yield larger gradients than a cross-entropy loss if the model predictions are very inaccurate. Also, particular custom loss functions might involve exponentials or polynomials that rapidly escalate the gradient when the predicted value is far from the target. If combined with a deep architecture, this can amplify exploding gradient issues.

Choosing a loss that is well-scaled for your problem is crucial. In classification, cross-entropy typically generates stable gradients. However, for specialized tasks like sequence-to-sequence learning or certain generative models, you might rely on custom objectives (e.g., adversarial losses, partial differential equation-based constraints, etc.). In these cases, a small mistake in the loss design can create large mismatch signals that lead to gradient blow-up. Another subtlety is that some tasks require multi-objective losses; if one objective has a very different scale than the others, the combined gradient can fluctuate dramatically, exacerbating instability.