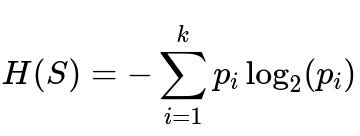ML Interview Q Series: When constructing a decision tree, in what way do you determine which feature is used to split at every node?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
A common approach in decision tree induction is to select the feature that maximizes some purity metric at each step. In practice, most algorithms (like ID3, C4.5, CART) use measures such as Information Gain, Gain Ratio, or Gini Impurity to evaluate the quality of each potential split.
Entropy and Information Gain
Entropy is a measure of disorder or impurity in the dataset. It quantifies the uncertainty in the distribution of class labels. A lower entropy value means the dataset is more “pure,” and a higher entropy value indicates the dataset is more “mixed.” For a set S with classes i = 1 to k, where p_i is the proportion of samples in class i:
where S is the current subset of samples we are measuring entropy for. Each p_i is the fraction of samples belonging to class i out of the total samples in S. If all samples in S belong to the same class, then p_i is 1 for some i and 0 for the rest, making the entropy 0. If samples are equally distributed among k classes, entropy is at its maximum value.
When deciding which feature X to split on, we measure Information Gain, which is the reduction in entropy from the parent node to the children nodes. We compute the expected entropy after splitting on a particular feature and see how much it decreases from the original entropy.
Gini Impurity
Decision Tree implementations such as CART often use Gini Impurity. This is another measure of how often a randomly chosen sample from S would be incorrectly labeled if we pick labels according to the distribution in S. It is calculated as follows for a set S with classes i = 1 to k:
where each p_i is the fraction of samples in class i out of the total in S. Similar to entropy, a lower Gini indicates higher purity. When evaluating a split on some feature X, we check the weighted Gini after the split and compare it to the Gini of the parent node, choosing the feature that achieves the largest reduction in Gini.
Gain Ratio
In some cases (notably in C4.5), a variant called Gain Ratio is used. It handles the bias that Information Gain sometimes has toward attributes with many distinct values. Gain Ratio adjusts the Information Gain by the “split information,” which measures how broadly the data is divided by a particular attribute. This is especially useful for attributes that might have as many unique values as there are samples.
Practical Splitting Criteria
In summary, at each node, the algorithm:
Calculates a purity metric (like entropy or Gini) on the current set.
Considers each candidate feature, splitting the data according to possible values of that feature.
Computes the resulting purity in each child node, then aggregates this into an expected measure of impurity for the split.
Chooses the feature whose split yields the largest decrease in impurity (or the largest Information Gain, or highest Gain Ratio, depending on the tree algorithm used).
This process is repeated recursively until stopping criteria (such as maximum tree depth, minimum samples per node, or a purity threshold) are met.
How does entropy relate to Information Gain when deciding on the best split?
Information Gain is defined as the difference between the entropy of the parent node and the weighted sum of entropies of the child nodes after a split. The more the entropy decreases from parent to children, the higher the Information Gain, and hence the more beneficial the split is deemed to be.
What is the difference between Gini Impurity and Entropy?
Both are measures of impurity. Entropy has roots in information theory and can be more computationally intensive due to the log operation, whereas Gini is often simpler to compute. In many empirical settings, they tend to produce similar results, although in practice Gini is slightly faster to compute. Some believe Gini may have a slight advantage in performance for classification tasks, but the differences are often minor.
What if an attribute has many distinct values—does that not influence the splitting criteria unfairly?
Yes, a pure Information Gain criterion can favor features that have many unique values (like an ID attribute), causing overfitting. To mitigate this, algorithms like C4.5 use Gain Ratio, which penalizes splitting on attributes that partition the data into many small segments.
How do we handle continuous features when we choose which attribute to split?
For continuous attributes, decision tree algorithms typically search for the best threshold that partitions the data into two subsets, e.g., feature < threshold and feature >= threshold. This threshold is selected to maximize purity in the resulting subsets, similar to how discrete attributes are handled.
How does overfitting come into play when using these criteria?
Purely selecting splits that maximize purity can grow very complex trees that perfectly classify the training set but fail to generalize. To counteract this, we may apply:
Early stopping criteria (limit tree depth or require a minimum number of samples in a node).
Pruning strategies, where subtrees that do not contribute significantly to performance on validation sets are trimmed.
Can we use different metrics like classification error as a splitting criterion?
Yes, theoretically. However, classification error is not as sensitive to changes in node impurity as entropy or Gini. Entropy and Gini detect smaller changes in distribution, making them more effective for identifying good splits earlier in the tree-building process. Classification error can sometimes lead to suboptimal splits or might require deeper trees to achieve the same performance.
Are there computational efficiency concerns for large datasets?
For large datasets, repeatedly calculating entropy or Gini for all features and thresholds can be time-consuming. Techniques like presorting continuous features, approximation methods, or distributed frameworks (e.g., parallelizing the splitting calculation) can be employed to handle big data efficiently.
Do tree ensembles change the way we select splits?
Methods like Random Forests still use the same metrics (e.g., Gini or entropy) but only consider a random subset of features at each split. This provides diversity among trees in the ensemble and helps reduce correlation between individual models.
How would you confirm that the chosen attribute indeed improves the model's performance?
One would often:
Check the split’s effect on a validation set (or via cross-validation) in terms of classification accuracy, F1-score, or other metrics.
Evaluate whether the split leads to overfitting by comparing training performance with validation performance.
This ensures that the chosen attribute meaningfully contributes to better generalization rather than just memorizing training specifics.