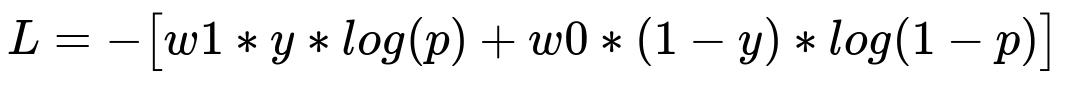ML Interview Q Series: When dealing with imbalanced datasets, what modifications or weighting strategies can be applied to the cost function to handle class imbalance? Give a concrete example.
📚 Browse the full ML Interview series here.
Hint: Focal Loss, weighted cross-entropy, and class-weighting in logistic/cross-entropy.
Comprehensive Explanation
Class imbalance occurs when one or more classes significantly outnumber the other classes in a dataset. This imbalance can lead to models that are biased toward predicting the majority class, ignoring the minority classes. To address this problem at the loss function level, the common strategies involve introducing class-dependent weights or modifying the shape of the loss function to penalize misclassification of minority classes more heavily.
One way to implement such strategies is to introduce weights into the standard cross-entropy or logistic loss. Another way is to modify the loss function using techniques like Focal Loss, which places increased focus on hard-to-classify examples.
Weighted Cross-Entropy
Weighted Cross-Entropy is a direct extension of the standard cross-entropy or logistic loss, with an additional weight that scales the loss for each class. For binary classification, the weighted cross-entropy can be written in a simple form where w1 is applied to the positive class, and w0 is applied to the negative class.
Here:
y indicates the true label, 1 for positive and 0 for negative.
p is the predicted probability of the positive class.
w1 is the weight for the positive (minority) class.
w0 is the weight for the negative (majority) class.
By choosing w1 > 1 relative to w0, the loss places greater emphasis on correctly classifying the minority class. This encourages the model to pay closer attention to examples from the minority class, reducing the effect of imbalance.
Focal Loss
Focal Loss is designed to tackle the problem of class imbalance by dynamically scaling down the loss contribution from easy examples and scaling up for hard or misclassified examples. The factor (1-p) in the term for a positive class misclassification (or p in the term for the negative class) is raised to the power gamma, which controls how heavily to down-weight easy examples.
Here:
alpha is a weighting factor for class imbalance (often between 0 and 1).
gamma >= 0 is the focusing parameter that adjusts how much to down-weight well-classified examples.
p is the predicted probability for the positive class.
y is the actual class label.
This loss function is especially popular in object detection tasks with highly imbalanced foreground vs. background classes.
Example of Applying Class Weights
Suppose you have a binary classification dataset where only 10% of the samples belong to the positive class and 90% belong to the negative class. The simplest weighting scheme is to invert the class frequencies, which sets w1 = 1 / freq(positive) and w0 = 1 / freq(negative). In this scenario, w1 would be 1 / 0.1 = 10 and w0 would be 1 / 0.9 ~ 1.11. You can scale these by any factor (the relative magnitude is what matters most).
Code Example
Below is a small Python snippet using PyTorch’s built-in weighted cross-entropy for a multi-class problem. For binary classification, the approach is similar but typically uses BCEWithLogitsLoss or a variation of cross-entropy.
import torch
import torch.nn as nn
# Suppose you have two classes, class 0 and class 1
# Let’s say class_0_weight = 0.3 and class_1_weight = 0.7
# Typically, you derive these from the class distribution in your dataset
class_0_weight = 0.3
class_1_weight = 0.7
weights = torch.tensor([class_0_weight, class_1_weight])
# Create a weighted cross-entropy loss function
criterion = nn.CrossEntropyLoss(weight=weights)
# Imagine a batch of predictions and targets
# predictions are raw logits (not probabilities) for each class
predictions = torch.tensor([[2.5, 0.3], [0.1, 1.0], [3.2, 0.2]], dtype=torch.float)
# targets must be the class indices, 0 or 1
targets = torch.tensor([0, 1, 0], dtype=torch.long)
loss_value = criterion(predictions, targets)
print("Weighted CrossEntropy Loss:", loss_value.item())
This code snippet demonstrates how to incorporate the class weights directly. For each sample in the batch, the loss for class 1 is scaled up by 0.7 while the loss for class 0 is scaled by 0.3. In practice, you might choose weights that reflect the ratio of class frequencies or an even more aggressive weighting for minority classes.
Potential Follow-up Questions
How can we select appropriate class weights for Weighted Cross-Entropy?
One common approach is to derive the weights from the inverse frequency of each class. For instance, if 10% of your samples belong to the positive class and 90% to the negative class, you can set the positive class weight = 1 / 0.1 = 10 and the negative class weight = 1 / 0.9 ≈ 1.11. However, there is no universal best way to set these weights; sometimes you might tune them as hyperparameters. If your minority class is very small and the resulting weight is extremely large, you might cause the training to overemphasize the minority class, so it can be beneficial to experiment with scaled versions of inverse frequency or other heuristics.
What is the difference between Focal Loss and Weighted Cross-Entropy?
Weighted Cross-Entropy simply rescales the loss of each class to give more importance to the minority class. However, once the class weight is set, it remains constant for every example belonging to that class. Focal Loss includes an additional factor that focuses more on harder examples. When gamma > 0, easy examples that are correctly classified with high confidence get their loss contribution down-weighted. This dynamic nature can be especially helpful in object detection tasks and other highly imbalanced settings where a large portion of examples are easy negatives.
How can class weighting be combined with other strategies like oversampling or undersampling?
Yes, you can combine sampling techniques with loss weighting. For instance, you might apply oversampling to the minority class (e.g., using SMOTE or random oversampling) and also use Weighted Cross-Entropy or Focal Loss for additional fine control. The key is to be mindful that aggressive oversampling combined with very high weights might lead to overfitting the minority class. Many practitioners conduct ablation studies to see whether weighting alone, sampling alone, or a combination works best for the specific task.
Can these methods be extended to multi-class imbalanced classification?
Yes, you can assign weights to each of the K classes in a multi-class setting, either by computing an inverse frequency for each class or using some domain-specific knowledge about class importance. Frameworks like PyTorch allow a weight tensor of size K for multi-class cross-entropy. Focal Loss can also be extended to multi-class tasks by applying the focusing factor to each class output.
Are there any caveats when using Weighted Cross-Entropy?
One potential caveat is that the gradient updates become more skewed toward improving performance on the minority class, which can sometimes degrade overall performance if the model ends up making too many false positives on the minority class. Another practical consideration is to check how your validation and test sets are balanced. If they are not representative, you might get a misleading picture of performance or incorrectly tune the weighting scheme. It is also a good practice to combine these weighting strategies with robust evaluation metrics such as confusion matrices, Precision-Recall curves, and the F1-score so that you do not rely solely on accuracy.
These strategies of weighting and loss modification are powerful tools for handling imbalanced datasets. They help shift the learning focus where it is most needed—on the minority or hard-to-classify examples—thereby improving the model’s overall performance on imbalanced tasks.
Below are additional follow-up questions
How can we ensure numerical stability when using extremely large or small class weights?
One common pitfall is that large class weights can cause the loss values to explode, leading to numerical instability or gradient overflow. For instance, if a dataset has a minuscule positive-class frequency, the corresponding weight might become very large. This can make the loss excessively sensitive to even small classification errors on the minority class.
A practical way to handle this is to normalize or clip the class weights. Some practitioners take the inverse frequency but then scale the weights by a constant factor so that they remain within a reasonable range (e.g., 0.5 to 3). Additionally, using stable optimizers such as Adam or RMSProp can help mitigate instability. Another approach is to ensure that the floating-point precision in your training framework supports the dynamic range of loss values, e.g., switching from float32 to float64 in extreme cases, though at a performance cost.
What happens if there are very few samples in the minority class, and how do we mitigate overfitting in such scenarios?
When the minority class has extremely few samples—on the order of tens or even less—applying large class weights or focusing heavily on that class can cause the model to overfit to those few examples. This can manifest as perfect classification of the minority examples in training but poor generalization for unseen data.
Several techniques can mitigate this:
Data Augmentation: For image data, applying transformations (rotations, crops, color jittering) can artificially increase the number of minority samples.
Oversampling with Caution: If you choose to oversample, ensure that you do not simply replicate the same examples; using techniques like SMOTE can create synthetic, slightly varied samples for the minority class.
Regularization: Strong regularization methods (e.g., dropout, L2 weight decay) help prevent the model from memorizing the few minority examples.
Cross-Validation: Evaluate your training using methods like stratified cross-validation to verify that the performance improvements generalize beyond the small minority set.
How do we handle partial or missing labels in an imbalanced dataset?
In some real-world scenarios, certain data points may have incomplete or uncertain labels, particularly for the minority class. Ignoring those samples might worsen the class imbalance even further, while making a naive assumption (e.g., treating missing labels as belonging to the majority class) can introduce biased training.
One approach is to use semi-supervised or weakly supervised learning techniques where unlabeled or partially labeled examples can be used to refine the decision boundary without fully relying on strict labels. Another strategy is to apply multi-task learning if there are auxiliary tasks that provide some extra information about unlabeled samples. For instance, if you know partial labels indicating the sample might be "suspected minority," you can incorporate that as a separate task.
Which evaluation metrics are best when using Weighted Cross-Entropy or Focal Loss for imbalanced datasets?
Accuracy can be very misleading with high class imbalance. Metrics like Precision, Recall, F1-score, ROC AUC, and PR AUC are typically preferred. Moreover, the following can add more insight:
Precision-Recall Curve: Particularly valuable because it focuses on the performance in the minority class region.
Confusion Matrix: Helps to see how minority and majority classes are getting confused relative to each other.
Macro-Averaged Precision/Recall: Averages metrics across classes, giving equal importance to minority and majority.
Weighted F1-score: Weights the F1-scores of individual classes by their support. This can be beneficial if you still want to reflect the overall distribution but also care about minority classes more than raw accuracy does.
How does mixing Weighted Cross-Entropy or Focal Loss with data augmentation techniques impact training?
Data augmentation can be especially beneficial in highly imbalanced scenarios, as it generates variations of the minority class, allowing the model to see more distinct (though synthetic) samples. However, you must pay attention to the combined effect of augmentation and loss weighting:
Risk of Over-Transformation: Overly aggressive image transformations can produce unrealistic samples that do not help the model generalize.
Consistency in Labeling: If you are mixing up images (e.g., Mixup) or applying transformations that blend images of different classes, you should ensure that labels are also properly updated. This is particularly important for minority classes where you cannot afford label noise.
Potential Overemphasis: If the class weights are already high and you generate a large number of augmented samples for the minority class, you could still create a bias that the model memorizes certain augmented minority examples rather than learning generally discriminative features.
In a production environment, how do we tune class weights or hyperparameters for Focal Loss?
In practice, hyperparameter tuning for Weighted Cross-Entropy or Focal Loss typically involves iterative experimentation:
Grid or Random Search: Over alpha and gamma (for Focal Loss) or over the class weighting distribution (for Weighted Cross-Entropy).
Automated Tools: Use Bayesian optimization or other advanced search strategies if computational resources allow, especially where the range of alpha and gamma is not well-known.
Early Stopping and Monitoring: Continuously monitor validation metrics (F1, PR AUC, etc.) as the model trains. If the model quickly overfits or the validation metrics start to plateau, that could indicate your weights are too large (or your gamma is too high).
Domain-Specific Intuition: Weights or gamma might be more or less sensitive in different domains (e.g., medical imaging vs. credit card fraud detection). Leverage domain knowledge to set sensible initial ranges.
Are there pitfalls when using Weighted Cross-Entropy or Focal Loss in regression tasks with heavily skewed target distributions?
Weighted Cross-Entropy and Focal Loss are classification-oriented. In regression tasks with skewed numeric targets (like a heavy-tailed distribution), these classification-specific losses do not directly apply. You might see misguided attempts to discretize a continuous target into bins and then apply Weighted Cross-Entropy, but this can introduce new challenges such as loss of resolution in the numeric targets.
For purely regression tasks with skewed targets, other techniques like transforming the target variable (e.g., log transform) or using quantile-based metrics might be more appropriate. If you do discretize the target, ensure that the binning approach is carefully designed to reflect the data distribution and that the weighting is applied in a way that truly addresses the underlying skew.
How do we apply these class weighting strategies or Focal Loss to multi-label classification problems?
In multi-label scenarios, each instance can belong to multiple classes simultaneously. You typically use a sigmoid output per label rather than a softmax over mutually exclusive classes. For Weighted Cross-Entropy, you can assign a separate weight to each label, depending on how frequent or important that label is. For Focal Loss, you adapt it by applying the focal term to each label independently:
Independent Sigmoid Outputs: Each output label has its own probability. You apply a loss function that sums (or averages) over all labels for each example.
Per-Label Weights: If label j is rarely present, you can set that label’s weight higher.
Careful Tuning: The interplay among different labels can be complicated. If certain labels co-occur, you might inadvertently over- or underemphasize them when combining weighting with multi-label correlations.
How does the size of the model or network architecture influence the effectiveness of Weighted Cross-Entropy and Focal Loss?
Larger or deeper networks might have more capacity to model minority class nuances, but they also might overfit more easily, especially with heavy class weighting. Smaller models might underfit if the imbalance is extreme, since they do not have sufficient capacity to represent minority-class nuances. Some considerations:
Regularization in Large Models: If you combine a large model with Weighted Cross-Entropy or Focal Loss, ensure strong regularization. This helps avoid overfitting on the minority class examples.
Architecture Choice: Sometimes simpler architectures with the right weighting or focusing strategy can outperform highly complex models that overfit.
Compute Constraints: Very deep networks also take more time to train, and the hyperparameter search for weighting factors might become computationally costly. You might do initial experiments on smaller models to find a ballpark range of weights before moving to production-scale networks.
How do you evaluate improvement in minority-class performance without hurting the majority-class performance too much?
This is a common dilemma. Boosting minority-class accuracy may degrade performance on the majority class. One strategy is to plot multiple metrics together, such as a precision-recall curve specifically for the minority class alongside overall macro- or weighted averages. Another approach is to define a business or domain-specific cost matrix that quantifies the trade-offs (e.g., how costly is a false negative on the minority class vs. a false positive on the majority class?). This matrix then helps you choose the weighting or focusing parameters that achieve the best trade-off according to real-world needs.