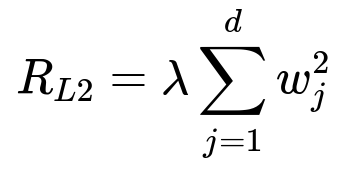ML Interview Q Series: When is L1-norm regularization more advantageous compared to L2-norm regularization?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Regularization techniques impose additional constraints or penalties on a model's parameters to combat overfitting. Both L1-norm and L2-norm regularization are widely used, but they exhibit distinct properties that make each suitable for different scenarios.
L1-norm Regularization (Lasso)
L1-regularization applies a penalty proportional to the absolute value of the weights. The penalty term can be expressed as:
Here, w_j denotes the jth parameter, d is the total number of parameters, and lambda is a hyperparameter controlling the strength of the regularization penalty. Because the penalty depends on the absolute values of the parameters, solutions often contain weights that are exactly zero. This leads to sparsity in the parameter vector.
L1-regularization is typically chosen when:
You require built-in feature selection. Zeroed-out weights effectively remove corresponding features.
You suspect that only a small subset of features truly contribute to model predictions (sparse models).
Interpretability is paramount, and you want a clearer understanding of which features are most influential.
L2-norm Regularization (Ridge)
L2-regularization applies a penalty proportional to the square of the weights. The penalty term is:
Because the penalty squares the weights, it discourages large parameter values but does not force them to become zero. L2-regularization spreads out weight adjustments more uniformly, reducing variance and improving numerical stability.
L2-regularization is typically chosen when:
You prefer to control the magnitude of parameters without driving them all the way to zero.
You need more stability in the presence of correlated features. L2-norm keeps all features (though shrinking them), often balancing correlated predictors.
You want to reduce the risk of overfitting in a situation where nearly all features have at least some minor contribution.
Choosing L1 vs. L2
You would favor L1 over L2 norm in the following scenarios:
Sparsity or Feature Selection: If you want to automatically discard irrelevant or redundant features, L1 is often preferred.
High-Dimensional Data: When the number of features far exceeds the number of samples, L1 helps isolate a small subset of important predictors.
Interpretability: L1 can produce a simpler model with fewer nonzero coefficients, which can be easier to interpret.
By contrast, you might still lean toward L2 if:
You do not necessarily need feature elimination but still need to reduce overfitting.
Your features are highly correlated, and you want to share shrinkage across them rather than picking one or few at random (as L1 might).
You seek smoother optimization since the L2 penalty is differentiable everywhere, while L1 requires subgradient-based methods or coordinate descent to handle the absolute value function.
Practical Example in Python
Below is a short code snippet using scikit-learn to demonstrate how one might use Lasso (L1-regularization) versus Ridge (L2-regularization) in linear modeling:
import numpy as np
from sklearn.linear_model import Lasso, Ridge
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# Generate some synthetic data
np.random.seed(42)
X = np.random.randn(100, 10)
true_w = np.array([3, 0, -1, 0, 2, 0, 0, 0, 0, 0]) # Sparse true weights
y = X.dot(true_w) + 0.1 * np.random.randn(100)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# Lasso Regression (L1)
lasso_model = Lasso(alpha=0.1) # alpha ~ lambda
lasso_model.fit(X_train, y_train)
lasso_predictions = lasso_model.predict(X_test)
lasso_mse = mean_squared_error(y_test, lasso_predictions)
# Ridge Regression (L2)
ridge_model = Ridge(alpha=0.1)
ridge_model.fit(X_train, y_train)
ridge_predictions = ridge_model.predict(X_test)
ridge_mse = mean_squared_error(y_test, ridge_predictions)
print("Lasso Coefficients:", lasso_model.coef_)
print("Lasso MSE:", lasso_mse)
print("Ridge Coefficients:", ridge_model.coef_)
print("Ridge MSE:", ridge_mse)
In many runs, the Lasso coefficients will have several exact zeros, illustrating its sparsifying nature. Ridge coefficients, on the other hand, will be mostly nonzero but smaller in magnitude compared to an unregularized solution.
What if you want both L1 and L2 properties?
The Elastic Net regularization combines L1 and L2 penalties. This is particularly helpful if you want to both select features (like L1) and still manage correlated variables more gracefully (like L2). Elastic Net blends these two properties by introducing a mixing parameter that balances the ratio of L1 and L2 penalties.
How does L1-norm achieve sparsity in practice?
L1 produces sparsity because it has a constant gradient magnitude whenever the parameter is nonzero. This can cause the parameter to be driven to exactly zero during optimization if the gradient is strong enough to overwhelm the parameter’s contribution. Mathematically, its absolute value function has a slope that does not diminish as w_j gets smaller (in contrast to the quadratic slope of L2 which goes to zero as w_j approaches zero).
Under what circumstances might L1 fail?
One potential pitfall of L1-regularization is in the presence of highly correlated features. The L1 penalty might zero out some features from a correlated set while leaving others with nonzero weights. This could lead to unpredictable behavior if domain knowledge suggests multiple correlated features are all valid. L2 typically handles this case more smoothly, shrinking correlated coefficients toward each other rather than arbitrarily eliminating some.
How do you tune the regularization strength?
Both L1 and L2 use a hyperparameter lambda (often called alpha in certain libraries) that determines how strong the regularization penalty is. You can tune lambda through approaches like cross-validation. A larger lambda increases the penalty, leading to simpler (and potentially underfitting) models; a smaller lambda lowers the penalty, which might allow overfitting.
Could L1 be combined with other forms of regularization or constraints?
Yes. Real-world scenarios might call for custom penalties or constraints. For instance, group lasso extends the L1 idea to enforce sparsity at the group level instead of the individual parameter level. Some practical implementations also impose monotonicity or other domain-specific restrictions while still incorporating L1 to encourage sparsity.
How does the gradient of L1 differ from L2 in implementation?
L2 has a straightforward derivative 2 * w_j for each parameter. L1's derivative is sign(w_j) if w_j != 0, and it is undefined at w_j = 0 (though in practice a subgradient approach is used, assigning a gradient in the range [-1, 1] when w_j = 0). Many machine learning frameworks handle this internally with coordinate descent or proximal gradient methods.
Summary of Key Takeaways
L1-norm (Lasso) is best when you want model sparsity and feature selection.
L2-norm (Ridge) is ideal when you want to shrink coefficients without forcing any to exactly zero, especially in correlated settings.
Sparsity can be extremely valuable for interpretability, computational efficiency, and dealing with high-dimensional data.
Mixing L1 and L2 (Elastic Net) can balance their respective advantages.