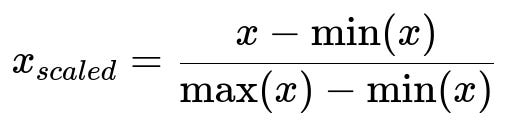ML Interview Q Series: When you want (and do not want) to scale or standardize a variable prior to model fitting?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Scaling or standardizing a variable generally means transforming the original values into a specific range or distribution. This often proves valuable in machine learning models that are sensitive to the magnitude of individual features (for example, distance-based methods). However, for certain classes of models, scaling can be less critical or even unnecessary. Understanding when to scale and when not to scale involves analyzing how the underlying learning algorithm treats feature magnitudes, how optimization is performed, and whether interpretability is a factor.
Core Mathematical Concepts
Scaling usually involves either standardization or normalization (min-max scaling). Standardization transforms values so that they have zero mean and unit variance:
Here x denotes the original value of the feature, mu is the mean of that feature over the dataset, and sigma is the standard deviation of that feature over the dataset.
Min-max scaling transforms each value into a [0,1] range by using:
In this expression, x is the original value, min(x) is the minimum value in the dataset for that feature, and max(x) is the maximum value for that feature.
When Scaling or Standardization Is Beneficial
One reason to scale is that many machine learning algorithms assume features share a similar scale or distribution. If features vary widely in magnitude, this can slow down or even destabilize training. Below are scenarios where scaling or standardizing helps significantly:
Distance-based Algorithms
Models like k-Nearest Neighbors, k-Means clustering, and support vector machines (especially with distance-based kernels such as RBF) rely on distance metrics. Unscaled features can dominate the distance calculations, thus biasing results towards features with larger numeric ranges.
Gradient-based Optimization
Algorithms that train via gradient-based methods (like logistic regression, linear regression with gradient descent, and neural networks) often converge faster and more reliably when features have comparable scales. Large feature values can lead to exploding gradients or unbalanced weight updates, whereas standardized inputs typically stabilize training.
Regularized Methods
Lasso (L1 regularization) and Ridge (L2 regularization) can behave more predictably if features have comparable magnitudes. Without scaling, a feature with very large values could overshadow other features during regularization.
Neural Networks
Neural networks, especially deep architectures, benefit significantly from input data that is normalized or standardized. This ensures that the initial range of activations is well-controlled, helping training converge more smoothly.
Feature Importance Comparison
When you want to compare the relative importance of features or interpret the scale of coefficients in methods that rely on coefficient values (like linear models), standardizing can help align your understanding of which features have more impact (though interpretability of the original units is lost).
When Scaling Is Not Necessary
Not all algorithms rely on feature magnitude. In certain cases, scaling or standardization may not be strictly required:
Tree-based Methods
Decision trees, random forests, and gradient-boosted trees split data based on feature thresholds. The magnitude of a feature has no bearing on how the algorithm finds optimal splits. Thus, scaling does not usually impact the final predictions.
Rule-based Methods
Methods like rule-based classifiers (for example, some variations of decision rules) do not rely on distance metrics or gradient-based optimization. The absolute scale is not a primary concern.
Purely Categorical Features
If a feature is purely categorical (especially if it is one-hot encoded), scaling does not apply in the same sense as for numeric data, because each dimension after encoding is just a binary indicator. Transforming 0/1 values to another range often does not provide additional benefits for distance-based or tree-based models, though for certain neural network settings, one might consider small transformations to binary indicators.
Interpretation in Original Units
Sometimes, you deliberately do not want to lose interpretability. In linear regression, for example, you may want to interpret the coefficient as "for every one unit increase in feature X, the response changes by some amount of Y." Standardizing or normalizing could conceal that direct interpretation in the feature’s original measurement units.
Practical Considerations
Handling Outliers
Standardization (subtracting mean, dividing by standard deviation) can be sensitive to outliers, since a few extreme values might inflate the standard deviation. If the dataset has outliers, robust scalers (using median and interquartile range) or ignoring outliers in the scaling calculation might be preferred.
Different Distributions
If one feature is expected to follow a normal distribution, and another is heavily skewed, a single universal approach may not be optimal. Sometimes log transformations or other domain-specific transformations offer better results than generic scaling.
Data Leakage
Scaling must be fitted only on training data. Then, the same transformation is applied to validation or test data. Otherwise, you risk leaking information about the distribution of the entire dataset into the training process.
Example in Python
import numpy as np
from sklearn.preprocessing import StandardScaler, MinMaxScaler
# Sample data: 2 features with vastly different scales
X = np.array([
[1, 1000],
[2, 800],
[3, 1200],
[4, 950]
], dtype=float)
# Standardization
scaler_std = StandardScaler()
X_std = scaler_std.fit_transform(X)
# Min-Max scaling
scaler_mm = MinMaxScaler()
X_mm = scaler_mm.fit_transform(X)
print("Original Data:")
print(X)
print("\nStandardized Data (mean=0, var=1):")
print(X_std)
print("\nMin-Max Scaled Data (range=[0,1]):")
print(X_mm)
Potential Edge Cases
Data with Extreme Skews
Features with heavy tails can degrade standardization. Consider log transforms or robust scalers.
Feature with Single Unique Value
If a feature has the same value for every row (variance=0), standard scaling can cause a divide-by-zero error. Typically, that feature is uninformative and might be dropped.
Sparse Data
When scaling sparse data (like word counts in text classification), standard methods could produce dense matrices. Specific care is needed to avoid memory issues.
Follow-up Questions
Could I use partial scaling on some features but not others?
Yes. You might selectively scale only the features whose magnitude differences could bias the model. Categorical or binary-encoded variables often do not need scaling, while numeric features on very different scales likely do. Also, domain knowledge can guide which features require normalization. If a feature already has a bounded scale (like a percentage from 0 to 100) or is on a consistent scale with others, it may be left as is.
Why might scaling be beneficial for neural networks beyond just faster convergence?
Neural networks often use activation functions (like ReLU, sigmoid, or tanh) that can saturate if inputs are too large or too small. Keeping the distribution of each input feature relatively similar helps the network more effectively learn internal weight parameters, avoid vanishing or exploding gradient issues, and maintain stable intermediate representations. Scaling also makes the initial gradient updates more uniform across different network layers, speeding up and stabilizing training.
Is scaling mandatory in linear or logistic regression?
While not always mandatory, scaling is frequently recommended for gradient-based solvers like stochastic gradient descent, because it can accelerate convergence. For methods using closed-form solutions (such as the normal equation in linear regression with small feature sets), scaling does not change the solution but can reduce numerical instability. For logistic regression with regularization, scaling usually simplifies the choice of regularization parameters and ensures each feature is penalized more uniformly.
How does standardization affect interpretability?
Once you standardize a feature, the learned model parameters or coefficients no longer correspond to changes in the original measurement units. Instead, they reflect changes in “standard deviations” of that feature. While this can be beneficial for directly comparing which features matter more (in the standardized space), it can become harder to communicate results outside the modeling context. If interpretability in the original units is crucial, you may prefer not to scale or to at least keep track of the inverse transformation.
What if the data contains outliers?
Outliers can inflate the mean and the standard deviation, leading to distorted standardized values. Using robust scalers (based on the median and interquartile range) or employing transformations (like logarithmic if the data is strictly positive) might be more reliable. Alternatively, outlier detection methods can be used to remove or cap extreme values before scaling.
In what cases might min-max scaling be preferred over standardization?
Min-max scaling ensures all features lie strictly within [0, 1] (or a chosen range). This can be advantageous if you know downstream algorithms or steps assume normalized inputs within a specific interval (e.g., certain image processing or transformations). However, min-max scaling is more sensitive to outliers than standardization. If your features must be in a bounded interval—perhaps for neural network inputs that assume [0, 1]—min-max scaling can be a straightforward solution, provided outliers are handled or do not exist.
Below are additional follow-up questions
Does scaling prior to performing PCA (or other dimensionality reduction methods) matter?
Performing Principal Component Analysis (PCA) or other linear dimensionality reduction methods like SVD relies on the covariance structure of the features. If different features vary in scale, the resulting covariance matrix can be dominated by features with larger magnitudes. This often leads to principal components that prioritize the features with higher numeric ranges, potentially obscuring useful variance in other features.
By scaling or standardizing features before applying PCA, you ensure that each feature contributes more equally to the variance-covariance structure. This typically leads to a more balanced extraction of principal components, each reflecting meaningful variance from a variety of features rather than being driven primarily by large-scale features.
A related pitfall is forgetting to apply the same transformation to new data. For example, if you perform PCA on training data that was standardized, you must also use the same scaling parameters (mean and standard deviation of each feature derived from the training set) to transform your test data. If you re-fit the scaler on the entire dataset (including test data) or forget to scale new data at all, your test features will be in a different scale domain than the training set, rendering the PCA components inconsistent.
How does cross-validation interact with scaling, and should I use different scaling for each fold?
When performing cross-validation, the standard approach is to split your data into k folds. For each training fold, you fit the scaler (computing means and standard deviations or min and max values) and transform the training data. Then, you apply that same transformation to the validation fold. This ensures that no information from the validation set influences the scaling parameters, thereby preventing data leakage.
A common pitfall is to scale the entire dataset (both train and validation) before performing cross-validation splits. This leaks validation data statistics (like mean and standard deviation) into the training process, artificially boosting performance estimates. Always fit the scaler solely on the training fold (or training subset) and use that same transformation for the validation fold.
How does scaling affect ensemble methods combining both distance-based and tree-based models?
Some ensemble methods might combine models that are sensitive to feature magnitude (like an SVM or k-NN) with tree-based models (like random forests). Tree-based models do not require scaling, but the distance-based models do. In such a setting, you typically still scale all numeric features, primarily for the distance-based learners.
From a practical standpoint, including tree-based methods in an ensemble that uses scaled features does not harm those tree-based models. They still will search for split thresholds just as before. Therefore, applying scaling consistently across all features and all models in the ensemble simplifies the workflow and prevents you from accidentally overlooking the needs of your distance-based or gradient-based components.
A subtle pitfall is if your implementation merges raw predictions or merges internal representations in an ensemble pipeline, you must confirm that consistent transformations are carried over. Mixing unscaled and scaled versions of the same data without a purposeful design might create confusion or degrade final performance.
How should you handle scaling or normalization differently for time-series data compared to i.i.d. data?
In time-series data, future observations should not affect the scaling parameters for historical observations, or you risk future-information leakage. One approach is a rolling or expanding window scaler: you compute scaling parameters (mean, standard deviation, min, max, etc.) only up to a specific point in time and then apply them to that time segment.
If you scale your entire time series using overall min and max from the entire dataset, you might introduce knowledge about future values into your current data transformation. This can lead to overly optimistic performance estimates. It is more rigorous to incrementally update your scaling parameters as you move forward in time, but carefully ensuring you never peek into the future data.
Another subtlety is seasonality. If your data exhibits strong seasonal patterns, the mean and standard deviation might shift over time. You may need to keep track of these shifts by recalculating scaling factors in a rolling window that aligns with your seasonality period.
What are the key differences among various robust scaling methods, and when might you prefer them?
Robust scaling typically downplays the influence of outliers by using statistics less sensitive to extreme values (like median and interquartile range instead of mean and standard deviation). Some common robust methods include:
RobustScaler (using median and interquartile range): Each feature is centered around the median, and scaled according to the interquartile range. This reduces the impact of extreme values.
QuantileTransformer: Transforms features to follow a uniform or normal distribution by mapping them to their corresponding quantiles. While powerful for addressing skew, it can distort the relative distances between data points in unexpected ways.
PowerTransformer (Box-Cox or Yeo-Johnson): Applies a power or log-like transform to stabilize variance and reduce skew, which can help if your data spans several orders of magnitude.
You might prefer robust scaling when your dataset has several outliers or heavy-tailed distributions, and you want to keep them in the dataset without letting them dominate standardization. However, robust methods can sometimes degrade performance if the outliers are truly informative or if the distribution is not heavily skewed. You also have to consider the interpretability of these transformations, as they can be less intuitive than standardization or min-max scaling.
Is it ever useful to apply multiple scaling transformations sequentially on the same feature?
Generally, you want to pick the transformation that most closely aligns with the data characteristics and the needs of your model, rather than stacking different scalers on the same feature. For example, applying standard scaling and then min-max scaling in sequence is redundant or contradictory. However, there are specialized scenarios in fields like image processing or signal processing where a domain-specific transform (e.g., log transform for spectral data) might be followed by a conventional standardization.
When combining transformations, you have to ensure each transform is truly adding value. Over-transforming the data can make it less interpretable and risk distorting meaningful relationships. Validate transformations systematically, for instance by checking model performance on a validation set, and confirm each step is justified by domain knowledge or empirical improvement.
Could scaling be dynamic during training if the data distribution shifts?
In an online learning context or streaming scenario where the data distribution changes over time, you might need to re-estimate scaling parameters on a regular basis or use an online approach to updating them. This can be done via a moving average and moving standard deviation, or a robust approach for median and interquartile range if outliers are expected.
A potential pitfall here is deciding how frequently to update these parameters. Updating too often can make the model overly reactive to noise, while updating too infrequently might cause the scaling to drift out of alignment with the true distribution. Also, each update must be applied carefully, ensuring you do not incorporate future data in the recalculation, preserving the temporal integrity of the scaling process.