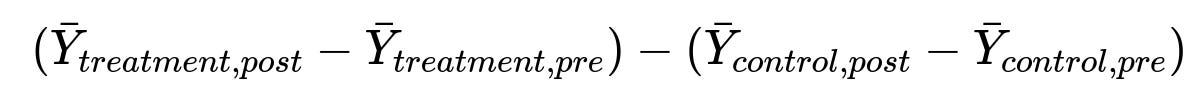ML Interview Q Series: Which factors would you consider significant for a push notification experiment, and should it be broadly rolled out?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
A standard approach when examining experimental results is to identify which metrics truly changed in a way that is both statistically and practically meaningful. In this scenario, a few typical performance indicators could be:
Engagement: Daily Active Users (DAU), session length, number of logins, or time spent in-app shortly after receiving the notification.
Trading Behavior: Frequency or volume of trades conducted following the push notification.
Revenue/Conversion Metrics: Any in-app purchase or transaction fees that might increase or decrease.
User Retention and Uninstall Rate: Whether push notifications cause fatigue, leading to uninstalls or push disablement.
Statistical Significance
To determine if these metrics are “significant,” analysts usually compare the control group (no notification) with the treatment group (notification). If certain metrics (like session length, average number of trades, etc.) show a measurable difference that surpasses a predefined threshold of statistical significance—often a p-value threshold of 0.05 or a desired confidence interval—then we can infer that the push notification has a genuine effect rather than random fluctuations.
For instance, if the primary objective is to see whether there is a difference in proportions (e.g., proportion of users who trade), one might apply a two-proportion z-test. A key formula for the test statistic in a difference of proportions is:
Where:
hat{p_1}is the proportion of a certain behavior (e.g., trades placed) in the treatment group.hat{p_2}is the proportion of the same behavior in the control group.hat{p}is the pooled proportion across both groups.n_1is the size of the treatment group, andn_2is the size of the control group.
If this statistic crosses a critical boundary (determined by the desired confidence level, e.g., 1.96 for 95% confidence), we conclude that there is a statistically significant difference in the proportion measure.
Practical Significance
Large sample sizes (like 1,000,000 participants) can render even trivial differences statistically significant. A difference might be real from a statistical perspective, yet minimal from a practical standpoint. So beyond p-values, we should check:
Effect Size: Even if it is statistically significant, is the improvement in engagement/trades large enough to justify potential user annoyance or development cost?
Confidence Intervals: A difference might be small but uncertain (wide interval) or consistently pointing in a positive direction (narrow interval).
Rolling Out to All Users
Deciding whether to extend push notifications to everyone hinges not only on statistical significance but also on potential benefits versus negative outcomes like push fatigue. Key concerns could be:
User annoyance leading to turning off push notifications or uninstalling.
Differences in behavior for newly installed users vs. those who have used the app for months. A certain user segment might still find the alerts valuable, while another might not.
Time zone variations: Market opens at a specific time, but user distribution is global. Some might receive notifications in the early morning hours, others in midday.
Balance of short-term vs. long-term effect: Over time, users who get frequent notifications might become immune or uninterested in them, causing novelty effects to fade.
If the experimental data shows clear improvements in user engagement, trading volume, or retention for the group that receives the notification—and the metrics such as uninstalls or opt-outs do not rise sharply—then rolling it out more broadly can be justified. However, if the effect size is very small or there are worrisome signals (like heightened uninstalls), a safer path is to iterate the messaging strategy or test with different user segments.
Potential Follow-Up Questions
How would you account for user-level factors like trading history or risk appetite?
You might segment users by their past trading behavior (e.g., active vs. passive investors) and track if the notification is more effective in driving re-engagement for casual users. Frequent traders might not need daily reminders, but occasional traders might find them helpful. By analyzing subgroups, we can see if the effect is consistent or varies.
What are possible confounding variables or biases?
One common pitfall is self-selection bias, where if the test is not strictly randomized, certain user types may naturally receive the notification. Historical trends can also confound results: if the market is going through unusual volatility, engagement changes might be driven by that rather than the push notification. Controlling for these factors is crucial (e.g., using random assignment, measuring baseline activity before the test, etc.).
How would you mitigate the risk of push notification fatigue?
Possible strategies:
Personalization: Send notifications only to users who have shown interest in early-morning trading or who are specifically active around market open.
Frequency capping: Ensure the user does not receive an abundance of app notifications in one day.
User feedback signals: Monitor if users are disabling notifications or ignoring them, then adjust accordingly.
If the experiment barely shows an overall positive impact, would you still roll it out?
This depends on the cost-benefit ratio:
Implementation cost: How difficult is it to maintain these push notifications?
Impact on user satisfaction: Even a small improvement might be helpful if it doesn’t degrade user experience.
Opportunity cost: If there are bigger features or push strategies with higher potential ROI, those might take priority.
How would you decide on alpha levels or confidence intervals for a large-scale experiment?
With very large sample sizes, tiny differences can yield p-values < 0.05. It’s common to lower alpha to something like 0.01 or 0.001 to filter out trivial differences. Alternatively, more emphasis could be placed on practical metrics such as minimum detectable effect or the cost of false positives.
How might you run future experiments around notifications?
Multivariate Testing: Different messages, times, or frequency.
Geographic or Demographic Segmentation: To observe if certain locales respond more positively to the notification.
Longitudinal Studies: Evaluating whether the effect diminishes after the novelty wears off.
Such experiments allow iterating on messaging strategy without risking the entire user base.
Below are additional follow-up questions
How would you determine the optimal sample size for such an experiment?
To decide how large each group (control versus treatment) should be, you can use typical power analyses. The goal is to ensure a high probability of detecting a true difference in key metrics if one exists (often aiming for 80% power or above). Factors to consider include:
Effect Size: A smaller effect size (like a tiny increase in engagement) will require a larger sample to detect reliably.
Variability of the Metric: If the metric of interest (e.g., trade volume per user) has high variance, you need more participants to gain clarity in results.
Significance Level (alpha): If you set a more stringent alpha, such as 0.01 instead of 0.05, the sample size generally must increase to maintain sufficient power.
Multiple Testing Corrections: If you test many metrics simultaneously (e.g., session length, purchase volume, times app opened), you may need to increase sample size to offset the risk of false positives.
A common approach for a continuous metric is to use known formulas or libraries like statsmodels in Python to compute needed sample sizes. Here’s a hypothetical code snippet:
import math
from statsmodels.stats.power import TTestIndPower
# Example parameters:
alpha = 0.05 # Significance level
power = 0.8 # Desired power
effect_size = 0.2 # Cohen's d or standardized difference
analysis = TTestIndPower()
required_n = analysis.solve_power(effect_size=effect_size, alpha=alpha, power=power, alternative='two-sided')
print(f"Estimated sample size per group: {math.ceil(required_n)}")
This helps ensure that your experiment’s groups are large enough to detect meaningful shifts in metrics.
How do you handle correlated metrics when deciding whether an experiment is successful?
Often, experiments do not revolve around just one metric (like daily active users); they might include session duration, trading frequency, retention, and more. These metrics can be correlated. For example, users who spend more time in the app might naturally trade more. The challenge is:
Inflated False Discovery: If you run multiple tests on correlated metrics, the chance of seeing at least one significant difference by random chance increases.
Choosing a Primary Metric: To avoid confusion, clearly define a single primary metric (e.g., percentage of users who trade) to gauge the main success criterion. Additional metrics become secondary or exploratory.
Multivariate Correction: Methods such as the Holm-Bonferroni procedure or Benjamini-Hochberg can adjust p-values to account for multiple correlated tests.
Joint Modeling: In some cases, you can set up a multivariate model that includes multiple correlated endpoints. This approach captures interaction effects between metrics, although it’s more complex.
Pitfall: If the most important metric does not show improvement, but a secondary metric does, there might be a temptation to declare victory anyway. Avoid “metric shopping.” Decide in advance which metrics are primary and which are supportive.
How might you assess the experiment’s impact on brand perception?
Though harder to measure, brand reputation can be significantly influenced by push notifications. Users receiving too many or poorly timed messages might find it annoying. Potential approaches:
In-App Surveys: Randomly sample users and ask if they find morning notifications useful or intrusive.
Social Media Sentiment Analysis: Track if push notifications trigger any changes in sentiment on Twitter, Reddit, or other forums where finance app users interact.
Net Promoter Score (NPS): Compare NPS or similar brand loyalty measures before and after the experiment. If heavy push notifications drive dissatisfaction, NPS may dip.
Edge case: A short-term increase in trades might be accompanied by a slow, steady decline in user sentiment. This negative brand perception can eventually cause churn. Hence, combining quantitative user metrics with qualitative feedback is essential.
How would you analyze a staggered launch approach to test different start times for the notifications?
Sometimes, sending notifications exactly at market opening might be suboptimal for certain time zones. A staggered launch approach sends notifications at different times for user segments. To evaluate results:
Segment the Population by Geographic Zone or Behavior: Some cohorts get the notification at actual market open, while others might get it an hour before. Compare engagement or trading behavior across these cohorts.
Difference-in-Differences (DiD): If you want to compare user activity in these staggered groups before and after the intervention while accounting for baseline differences, you can use a DiD approach. The core calculation for a simple DiD model can be expressed as:
Where:
bar{Y}_{treatment,post}is the average outcome (e.g., trades per user) for the treatment group in the post-intervention period.bar{Y}_{treatment,pre}is the average outcome for the treatment group in the pre-intervention period.bar{Y}_{control,post}is the average outcome for the control group in the post period.bar{Y}_{control,pre}is the average outcome for the control group in the pre period.
This helps control for ongoing trends that affect both groups and isolates the effect of the new notification timing.
How would you identify and handle novelty or “Hawthorne” effects in this experiment?
A novelty effect (or Hawthorne effect) occurs when users change their behavior simply because they know they are being observed or have something “new” happening. After a while, excitement can wane, and usage might revert to baseline. Strategies to detect and mitigate:
Extended Observation Window: Run the experiment long enough (beyond just a few days) to watch for any dip back to baseline.
Repeated Measurements: Track weekly trends. If improvements fade quickly (e.g., after two weeks), you might attribute a portion of the initial uplift to novelty.
Delayed Launch Group: Include a group that receives notifications later, so you can compare the immediate effect for the newly treated group with the sustained effect for those who’ve been receiving it for a while.
Pitfall: Basing decisions on short-lived increases might lead to overestimating the true long-term benefit.
How would you design a mechanism to let users opt into or out of these notifications, and still assess the impact of the experiment?
Allowing users to choose their preference is good for user satisfaction, but it introduces self-selection bias (users who want notifications might differ fundamentally from those who don’t). Potential approaches:
Encouraged “Opt-In” Experiment: Randomly show different prompts encouraging users to opt in to notifications. Compare outcomes between those shown the “encouragement” prompt and a control group.
Instrumental Variable Methods: If you have a random “push” to opt in, that random assignment can act as an instrument for the actual behavior (opting in or not), helping disentangle the causal effect of notifications from self-selection.
Hybrid Model: Enable full random assignment for a subset of users (those who have never set any preference), and track them to see the effect of forced treatment vs. forced control. Another subset can have the freedom to choose. That helps measure real-world usage while preserving some causal insight.
Edge case: If the majority of users opt out, you may see minimal overall effect, even if notifications are beneficial to those who remain subscribed. Always consider what fraction of users genuinely engage with these alerts.
How do you handle technical glitches or partial rollouts that occur during the experiment?
In large-scale deployments, not all targeted users might receive notifications due to server issues, mobile OS constraints, or missed registrations. This can skew results. Recommended strategies:
Intent-to-Treat (ITT) Analysis: Users who were assigned to the treatment but never actually received the notification (due to technical errors) are still considered in the treatment group. This preserves randomization integrity and reveals the “real-world effectiveness.”
Per-Protocol Analysis: Analyze only those who definitely received the notification as expected. This shows an “ideal” scenario effect but breaks random assignment and can introduce bias if the reasons for not receiving the push are non-random.
Monitoring and Logging: Track success/failure rates of notification delivery. If these rates are low, revisit infrastructure or message timing to ensure the test reflects real conditions.
Pitfall: If a large proportion of users never received the treatment, your observed “treatment effect” might diminish, and the power of the study can be compromised.