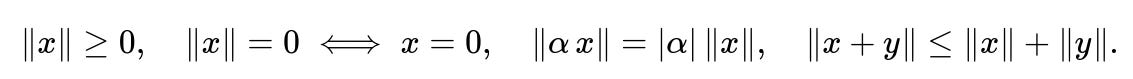ML Interview Q Series: Which fundamental properties must a function fulfill in order to qualify as a norm?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
A norm is a function that assigns a nonnegative real value to vectors in a vector space, reflecting the notion of “size” or “length.” The following four conditions must be satisfied. These conditions capture non-negativity, definiteness, homogeneity, and the triangle inequality. One way to represent them together in symbolic form is shown below.
Below is an inline textual explanation of each parameter:
x and y are vectors in a vector space.
alpha is any scalar (real or complex, depending on the underlying field).
|alpha| is the absolute value (or modulus) of alpha.
norm(x) denotes the norm of vector x.
These properties ensure that the function truly captures all the intuitive aspects of length. Non-negativity and definiteness (the first two conditions) guarantee that there is no concept of “negative length,” and only the zero vector has norm zero. Homogeneity (the third property) ensures scaling by alpha directly scales the norm by the absolute value of alpha. The triangle inequality (the fourth property) ensures that the norm of the sum of two vectors does not exceed the sum of their norms, mirroring the intuitive geometric idea of how the sides of a triangle relate to each other.
A classic example is the Euclidean norm in R^n, defined in plain text form as sqrt(x1^2 + x2^2 + ... + xn^2). Other examples include L1 norm or L_infinity norm, each satisfying the same four basic properties but measuring length differently.
Potential Misinterpretations
Some might conflate norms with other concepts like metrics. Though related, a metric has a weaker requirement: d(x, y) must measure distance between points x and y in a space, whereas a norm is specifically a distance-from-origin measure that induces a metric by defining d(x, y) = norm(x - y).
Another common oversight is ignoring the absolute value in the homogeneity property. Failing to take the absolute value leads to violation of the norm definition in the case of negative scalars.
Follow-up Questions
How does a seminorm differ from a norm?
A seminorm lacks strict definiteness. In other words, a seminorm p(x) can be zero for nonzero x. It still satisfies non-negativity, homogeneity, and the triangle inequality, but it might not fulfill the condition p(x) = 0 if and only if x is zero. This is often seen in functional analysis, where seminorms are used as intermediate tools before constructing full normed spaces.
Why does the scaling property use the absolute value of the scalar?
The goal of a norm is to measure “length” rather than track any sense of direction or sign. If alpha were negative, failing to use the absolute value would allow the norm to become negative, which contradicts the non-negativity property. By using |alpha|, we capture how scaling a vector by alpha changes its length but not the positivity of the length.
Can a norm induce a metric on a vector space?
A norm on a vector space induces a distance function (a metric) through d(x, y) = norm(x - y). This meets all metric axioms:
d(x, y) >= 0.
d(x, x) = 0.
d(x, y) = d(y, x).
d(x, z) <= d(x, y) + d(y, z). That final requirement is a direct consequence of the triangle inequality for norms.
Do all norms come from inner products?
Not every norm arises from an inner product. Those that do must satisfy the parallelogram law, which states 2 * (norm((x + y)/2)^2 + norm((x - y)/2)^2) = norm(x)^2 + norm(y)^2. If the parallelogram law holds, then the norm is induced by an inner product. Otherwise, it is still a valid norm but not necessarily tied to any underlying inner product.
What are some pitfalls in real-world applications?
In practice, one must be careful about numerical stability and representation. For example, high-dimensional vectors with large coordinate values might lead to numerical overflow when squared, especially in Euclidean norm calculations. Sparse data representations can also change how we compute norms, favoring norms like L1 for interpretability and computational efficiency. Ensuring these four properties hold allows you to apply well-defined geometric or optimization-based methods.
Could you show a brief code snippet to compute different norms in Python?
import numpy as np
def l1_norm(vector):
return np.sum(np.abs(vector))
def l2_norm(vector):
return np.sqrt(np.sum(vector**2))
def linf_norm(vector):
return np.max(np.abs(vector))
# Example usage:
v = np.array([3, -4, 2])
print("L1 norm =", l1_norm(v)) # 3 + 4 + 2 = 9
print("L2 norm =", l2_norm(v)) # sqrt(9 + 16 + 4) = sqrt(29)
print("Linf norm =", linf_norm(v)) # max(|3|, |4|, |2|) = 4
Each of these examples satisfies the four norm-defining properties listed earlier, though they measure “size” differently.