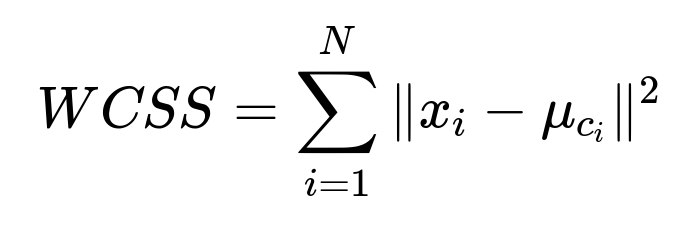ML Interview Q Series: While using K-means clustering, how can we decide on the optimal value of k (number of clusters)?

📚 Browse the full ML Interview series here.

Short Compact solution

One widely adopted way is the elbow method, which involves plotting the explained variation or within-cluster sum of squared distances against different values of k. As k increases, the total within-cluster variation drops, but at some point this decrease becomes more gradual. That point, which often looks like an “elbow” in the curve, is taken as a sensible choice for k. Another frequently used approach is the silhouette method, which measures how well each sample fits within its assigned cluster compared to other clusters. Higher silhouette scores indicate better-defined clusters. Finally, real-world insight or business considerations can also guide the selection of k, since there is rarely a single, perfect mathematical approach that works for every dataset or domain.

Comprehensive Explanation

A fundamental challenge in K-means clustering is determining the number of clusters, k. The dataset itself will not always suggest a clear number of natural groupings, and K-means can produce different clusterings for different k values. Below are key ideas behind choosing k and how they work in practice.

Relationship Between k and Variation

K-means attempts to minimize the total within-cluster sum of squared distances between points and their cluster’s centroid. This quantity is often referred to as the Within-Cluster Sum of Squares (WCSS). The objective is to find cluster centroids that minimize this metric across all clusters.

where ( x_i ) is the ( i )-th data point, and ( \mu_{c_i} ) is the centroid of the cluster ( c_i ) to which ( x_i ) belongs.

When k increases, WCSS generally decreases because more clusters means each centroid can be positioned to reduce the distances within its cluster. However, if k is too large, you may over-partition the data (possibly isolating individual points as their own clusters). This is why we look for an optimal balance that offers sufficiently low WCSS without overfitting.

Elbow Method

The elbow method typically involves the following steps:

Plot the WCSS (or a related measure of cluster variance) for various k values. Observe how the curve changes as k increases. Locate a point beyond which adding more clusters yields diminishing returns in decreasing WCSS.

If an obvious “elbow” or sharp corner is visible, that usually marks a strong candidate for k. However, in some cases, the curve can be smooth or show multiple bends, making the choice less clear. This ambiguity can be common in high-dimensional data or data that doesn’t have clearly defined separations.

Silhouette Method

The silhouette coefficient evaluates how similar each point is to points in its own cluster relative to points in other clusters. For a data point (i), let (a_i) be the average distance to other members of the same cluster, and let (b_i) be the average distance to the nearest cluster’s members. The silhouette coefficient (s_i) is defined as:

A silhouette coefficient near 1 indicates the sample is appropriately assigned to its cluster, a value near 0 suggests the sample is on the boundary between two clusters, and values below 0 suggest possible misassignment. By computing an average silhouette score across all points for different k values, one can select k that maximizes this average silhouette value. Although robust, the silhouette method is more computationally demanding for large datasets because it requires distance computations among points across clusters.

Domain Knowledge and Visualization

Choosing k also benefits from domain-specific context. For instance, if the dataset represents different customer segments, there might be an expectation of how many distinct segments are meaningful from a business standpoint. Visualizations such as Principal Component Analysis (PCA) projections can also help identify potential group structures or highlight whether the data forms continuous variations rather than distinct clusters.

Caveats and Practical Considerations

In real-world datasets, there is not always a single best k. The decision might require a combination of technical methods (elbow or silhouette) and practical insight (domain knowledge, interpretability, etc.). If the data does not separate cleanly, these metrics may not reveal an obvious elbow or a well-defined maximum silhouette score. Sometimes no clear “drop” or “peak” appears. Additionally, K-means assumes clusters with roughly spherical shapes and similar sizes. If the dataset’s structure is non-spherical or has clusters of very different densities, the standard K-means algorithm’s notion of sum-of-squared distances might not capture the best grouping, and the methods for finding an optimal k might be misleading.

Follow-up Question: Why does the elbow plot sometimes fail to reveal a clear elbow?

Elbow plots can fail to produce a distinct corner if the dataset is either composed of overlapping clusters or if the total variation decreases steadily without a single large inflection. Real data might form complex structures or have several clusters that merge into each other in ways the simple K-means assumption does not capture. In such cases, the curve of within-cluster variation versus k may appear smooth, and no single point stands out. Practitioners typically combine the elbow approach with other diagnostic methods, such as examining silhouette scores or applying domain knowledge to see if certain cluster counts are more meaningful for the application.

Follow-up Question: What if the data is not well-suited to spherical clusters?

K-means can struggle with elongated, non-convex clusters, or clusters of dramatically different sizes, because it optimizes distance to centroids. One workaround is to transform or engineer features so clusters become more spherical in feature space. Alternatively, one could switch to algorithms designed for more general cluster shapes, such as DBSCAN or hierarchical clustering. However, if K-means remains the chosen method, the discovered “optimal” k might represent only a local optimum that fits the spherical-cluster assumption.

Follow-up Question: How do we implement the elbow and silhouette methods in Python efficiently?

Both methods can be explored using libraries like scikit-learn. Below is a rough, unnumbered code outline demonstrating how to do an elbow plot and compute silhouette scores:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score

# Suppose X is your dataset as a NumPy array
# Elbow method: compute within-cluster sum of squares for k in [2..max_k]
wcss_scores = []
max_k = 10
for k in range(2, max_k+1):
    kmeans = KMeans(n_clusters=k, random_state=42).fit(X)
    # inertia_ is the sum of squared distances within clusters in scikit-learn
    wcss_scores.append(kmeans.inertia_)

# Plot elbow
plt.plot(range(2, max_k+1), wcss_scores, marker='o')
plt.xlabel("Number of clusters (k)")
plt.ylabel("Within-Cluster Sum of Squares (WCSS)")
plt.title("Elbow Method")
plt.show()

# Silhouette method: compute silhouette scores for k in [2..max_k]
silhouette_scores = []
for k in range(2, max_k+1):
    kmeans = KMeans(n_clusters=k, random_state=42).fit(X)
    labels = kmeans.labels_
    score = silhouette_score(X, labels)
    silhouette_scores.append(score)

# Plot silhouette scores
plt.plot(range(2, max_k+1), silhouette_scores, marker='x', color='red')
plt.xlabel("Number of clusters (k)")
plt.ylabel("Average Silhouette Score")
plt.title("Silhouette Analysis")
plt.show()

In real scenarios, you might try a larger range for k or tweak initialization parameters for K-means (like “n_init” in scikit-learn) to ensure more stable cluster assignments. You can also combine these plots with domain knowledge, or do extra steps like visualizing the distributions in each cluster.

Follow-up Question: If the dataset is huge, how can we scale these methods?

Computing distances for silhouette scores can be expensive in very large datasets. A common strategy is to use a representative sample of data instead of the entire dataset when computing silhouette coefficients. Techniques like mini-batch K-means can also speed up clustering, approximating standard K-means while coping better with large volumes of data. Additionally, applying dimensionality reduction (e.g., PCA) before clustering can reduce computational overhead, though one has to confirm that the compressed representations preserve enough critical structure to form reliable clusters.

Follow-up Question: What if multiple k values give similar metrics?

This could happen if the data supports multiple plausible cluster resolutions, or if the dataset has substructures that can be validly clustered at different scales. In practice, choosing among these k values depends on your application requirements or how you plan to interpret or use the clusters. You might pick the smaller k for simpler interpretation, or the larger k if you need more granular groupings. Often, you will also check how stable clusters remain across different random initializations. If multiple k values produce consistent, equally good clustering, business or domain context often settles the final choice.

Below are additional follow-up questions

How do random initializations in K-means impact the choice of k?

Random initialization can influence how cluster centroids are placed at the start of the K-means process. If the data has complex structure or if the initial centroids are poorly positioned, the resulting within-cluster sum of squares (WCSS) might be higher or lower for a particular k than it otherwise would be with better centroid seeds. This can lead to misleading elbow plots or different silhouette scores, potentially causing you to pick a suboptimal k.

In real-world applications, a common practice is to run K-means multiple times with different random seeds (the “n_init” parameter in popular libraries) and take the run that yields the best overall clustering metric (e.g., the lowest WCSS). By doing so, you reduce your risk of being misled by unlucky initialization. You might also use specialized initialization strategies such as k-means++ to improve centroid placement, although even that does not guarantee avoiding local minima in every scenario.

Pitfall: If the data is large, you may be tempted to reduce the number of times you run K-means to save computation time. Fewer runs mean a higher chance of poor initial seeds influencing the results, so it’s vital to balance the computational budget with sufficient random restarts to ensure a robust outcome.

What if new data arrives over time and shifts the underlying distribution?

Real-world datasets often evolve. For instance, user behavior can change, new products can appear, or sensor inputs can drift. If you initially pick a certain k based on a snapshot of data, that choice may become suboptimal as the distribution shifts. In practice, you might need to re-run your clustering periodically or develop an online or incremental clustering approach that adapts to new data.

A practical strategy:

1. Schedule periodic model updates and recalculations of WCSS or silhouette scores to see if the original k remains suitable.

2. Consider methods like mini-batch K-means or streaming variants of clustering that allow continuous updates.

3. Continuously track cluster characteristics (e.g., cluster sizes, average distances) to detect significant drift.

Pitfall: Failing to notice data drift can result in outdated clusters that no longer reflect the true relationships in your data. This issue is particularly serious in domains like e-commerce, user behavior analytics, or time-series data from sensors.

Does the presence of outliers skew the elbow or silhouette method?

Outliers can disproportionately affect K-means since the algorithm attempts to minimize squared distances. A single outlier can shift the centroid significantly, especially in smaller clusters, leading to inflated within-cluster sums of squares. Consequently, the elbow or silhouette analyses might show suboptimal or misleading patterns.

Mitigation strategies:

• Outlier detection and removal (or capping) before clustering.

• Using robust distance metrics (e.g., using a different clustering algorithm more tolerant to outliers, such as DBSCAN or Gaussian Mixture Models with robust covariance estimates).

• Applying feature transformations like log-scaling or standardization so that extreme values exert less undue influence.

Pitfall: In many business contexts, outliers could represent critical cases (e.g., fraudulent transactions or VIP customers). Automatically removing them might lose important insights. Always check whether those “outliers” contain valuable information before you decide to filter them.

Could interpretability concerns dictate how we select k?

Interpretability plays a significant role in deciding the number of clusters, especially in fields like healthcare or finance where you need clear explanations for why each group exists. Even if mathematical methods point to a certain k, stakeholders might prefer fewer clusters that are easier to interpret. For instance, a hospital might want 3 risk groups rather than 10, even if 10 yields a slightly better WCSS or silhouette score.

Pitfall: Sacrificing too much clustering quality for the sake of a low-dimensional explanation can overlook meaningful subgroups. On the flip side, picking a high k might produce complicated groups that are too fine-grained to be practical. Balancing interpretability with mathematical rigor is usually solved with close collaboration between data scientists and domain experts.

Are there other methods like the gap statistic that can supplement the elbow or silhouette methods?

Yes. The gap statistic method is another approach to estimate the number of clusters. It compares the within-cluster dispersion of your actual data with that of reference data (generated under a null hypothesis of no obvious cluster structure). If there’s a significant difference in the dispersion, it suggests that your data exhibits substantial clustering. By running this comparison for various k values, you can find a k that maximizes the gap between real and reference dispersion.

In certain scenarios, the gap statistic can be more robust than the elbow method, especially if the elbow plot is ambiguous. However, the gap statistic itself can be computationally heavy, since it typically requires multiple runs on both real data and synthetic reference data. It also depends on how you generate the reference distributions, which can sometimes be tricky for very high-dimensional data.

Pitfall: If the reference data you generate doesn’t reasonably mimic the real data’s bounding region or distribution, the comparison could be off. Additionally, the method can become computationally expensive for large datasets, and parameters need to be tuned carefully to ensure it’s a fair comparison.

Does dimensionality reduction before clustering affect the choice of k?

In high-dimensional datasets, distance measures become less meaningful (the curse of dimensionality). Many practitioners therefore apply dimensionality reduction (e.g., PCA, t-SNE, or UMAP) to compress the data into a smaller number of dimensions before performing K-means. While this can help the algorithm find more meaningful clusters, it also changes the feature space, which may shift where the “elbow” or the maximum silhouette occurs.

If you’ve reduced your features from, say, 500 to 10 principal components, the distance relationships among points might be fundamentally altered. This might affect the location of the elbow in your WCSS plot or how the silhouette coefficients distribute. You may discover, for instance, that the best k in the reduced space is smaller than it was in the original space, simply because the main variation is captured in fewer dimensions.

Pitfall: Overly aggressive dimensionality reduction might merge distinct groups or hide small but important variations. Underly cautious dimensionality reduction (e.g., using too many principal components) might not alleviate high-dimensional noise enough to reveal good clusters.

How could we handle categorical or mixed-data types in K-means when determining k?

Standard K-means is best suited for continuous, numerical features, primarily because it relies on Euclidean distances. For categorical or mixed-type data (part categorical, part numerical), basic K-means may not be appropriate, making the elbow or silhouette methods less meaningful if used with Euclidean distance on purely categorical attributes. Specialized algorithms—like K-modes for categorical data—have different cost functions and distance measures.

When dealing with mixed-data:

1. Convert categorical features into numerical encodings (like one-hot encoding or embeddings).

2. Use distance measures more suited to categorical attributes (e.g., Hamming distance).

3. Consider alternative clustering algorithms (e.g., hierarchical with an appropriate linkage method) that can handle mixed distances.

Pitfall: Forcing K-means on data with primarily categorical variables often leads to misleading cluster centroids, especially if the encoding scheme inadvertently exaggerates certain categories. Also, if your encoding is too high-dimensional (like extensive one-hot vectors), the curse of dimensionality might degrade distance metrics.

Does K-means always converge to the same clusters for a given k?

Not necessarily. K-means is a local search algorithm that depends heavily on initial centroid placement. Even with the same k, two runs of K-means can produce different final clusters if they begin with different seeds. In practice, it’s common to run K-means multiple times and select the clustering with the best objective value (lowest WCSS). However, there’s no guarantee you’ve found the global minimum. If the dataset has many local minima, you can end up with slightly different partitions.

Pitfall: If the data is very large, repeated runs become expensive. Some people settle for fewer runs, but risk missing better cluster configurations. Failing to replicate your results with multiple seeds also might hamper the reliability of your chosen k, especially if the elbow and silhouette scores vary significantly from run to run.