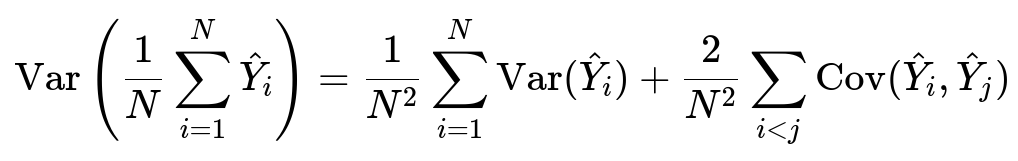ML Interview Q Series: Why do ensemble methods typically achieve better performance when their constituent models have low correlation?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

Ensemble methods combine multiple base learners to produce a single predictive model with higher accuracy, robustness, and generalization capacity. One major reason these techniques excel is their ability to reduce overall variance when the individual models’ errors are not highly correlated with each other.

When base learners share similar mistakes or are heavily correlated in how they make predictions, the ensemble might not deliver substantial gains in overall performance. On the other hand, if their errors differ substantially (indicating low correlation among models), the averaging or voting process tends to cancel out individual weaknesses, producing a more reliable final prediction.

A helpful perspective is to look at the variance of the ensemble prediction. For an ensemble of N models, let each model’s prediction be denoted by hatY_i. The ensemble prediction can be considered as the average of all individual predictions. A key mathematical formula for the variance of the mean of multiple random variables (under some simplifying assumptions) is shown below.

Here, hatY_i is the random variable representing the prediction from model i. N is the total number of models in the ensemble. Var(hatY_i) is the variance of the prediction from model i, and Cov(hatY_i, hatY_j) is the covariance between predictions from models i and j.

The expression reveals that when the models have low correlation, their covariances are small, making the second summation term significantly reduced. Consequently, the variance of the ensemble’s average is lower compared to the variance of each individual model. This typically leads to improved prediction stability and better generalization.

Models can have low correlation if they are trained on different subsets of data (as in bagging), different features (feature sub-sampling in random forests), or different target transformations. They can also be forced to reduce correlation by introducing randomization at various stages of training or by using diverse model architectures (e.g., mixing decision trees, neural networks, and linear models).

Ensuring the models are diverse helps the ensemble to “hedge its bets” across different kinds of patterns. If one model fails in a certain pattern region, another model that does not share that failure can mitigate the overall error.

How do you measure correlation among models in practice?

One common approach is to make predictions on a fixed validation set or out-of-bag data for each base learner. Then you can compute either the Pearson correlation coefficient or look at other similarity metrics among the prediction vectors. For classification tasks, you can also consider how frequently two models make the same incorrect predictions. The idea is that if two models are perfectly correlated, their prediction vectors will be almost identical on the validation set, offering little variance-reduction benefit when averaged. If they are only weakly correlated, you observe a larger net gain from combining them.

What if the models are too uncorrelated or produce contradictory predictions?

If base learners are extremely different and contradictory, the ensemble might become unpredictable in regions where these contradictions arise. Although low correlation is generally desirable, it must be combined with each model having a reasonable level of individual accuracy. If some models are effectively “guessing,” then including them might inject random noise, potentially degrading the ensemble’s performance. The goal is to ensure each base learner is better than random guesswork, while still maintaining diversity in how each model arrives at its predictions.

Can correlation alone determine ensemble performance?

Correlation is a key piece of the puzzle, but not the entire story. The bias and variance of each individual model also matter. If every base learner is poorly fit and has high bias, simply combining them may not produce a good result, even if they have low correlation. In ensemble theory, it is often said that each model should be “accurate and diverse.” Accuracy refers to having at least moderately strong predictive power (low bias) and diversity is related to ensuring that the models are not all making the same mistakes (low correlation).

Which methods can be used to reduce correlation among ensemble models?

There are several strategies:

• Randomizing the training data by subsampling (bagging): Each model is trained on a different bootstrap sample of the data, which creates diversity.

• Randomizing features (random forests): Each tree is trained on a subset of features, reducing correlation and promoting diverse splits.

• Using different base architectures: For instance, combining gradient boosting machines with neural networks can reduce correlation if they capture different patterns.

• Stacking or blending: Where one model’s predictions are used as features for another. This can reduce correlation if the meta-model corrects for systematic errors of the base learners.

What are practical strategies for ensuring low correlation among base learners?

You can experiment with different hyperparameters or use different data subsets or feature subsets during training. This ensures that each learner is exposed to varied training conditions. Another practice is employing early stopping or different initializations (particularly useful in neural networks) so that each model’s convergence path differs. Using cross-validation-based out-of-bag estimates to select only the models that disagree the most (but still maintain acceptable accuracy) is another targeted way to manage correlations.

All these techniques balance the need to have strong individual models (low bias) with the requirement that they not mirror each other’s mistakes (low correlation).