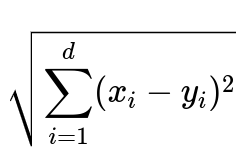ML Interview Q Series: Would you use K-NN for large datasets?

📚 Browse the full ML Interview series here.

Comprehensive Explanation

K-Nearest Neighbors (K-NN) is a non-parametric method that essentially memorizes the entire training dataset. When a new data point needs to be classified or regressed, K-NN searches for the K closest data points (neighbors) in the training set, then aggregates their labels in some way (e.g. majority vote for classification or average for regression).

One of the primary considerations with K-NN is the distance metric used to measure similarity between two points. A common choice is the Euclidean distance. In d-dimensional space, the Euclidean distance between x and y can be expressed as:

where x_i and y_i are the i-th features of the vectors x and y respectively, and d is the dimensionality of the data. This formula essentially measures the straight-line (L2) distance in d-dimensional space.

While straightforward and intuitive, the downside of K-NN is that it can be expensive to run for large datasets. The core issue is that the method requires scanning through all training examples to find the nearest neighbors for each new data point. If you have N data points and a dimensionality of d, a naive distance computation approach leads to high inference latency, since for each query you may need to compute distances to all N points in d-dimensional space. Memory usage is also large because K-NN needs to store the entire dataset.

Hence, if the dataset is massive, naive K-NN often becomes prohibitive in both computational cost and memory requirement. There are optimizations and techniques like approximate nearest neighbor search, dimensionality reduction, and specialized data structures (e.g. KD-trees, Ball trees, VP-trees) that can make K-NN more tractable, but even those have limitations, especially in high-dimensional data. Therefore, unless these specialized optimizations are employed, using K-NN directly on very large datasets is typically not recommended.

How to Overcome K-NN Challenges for Large Datasets

One common approach is to reduce dimensionality before performing K-NN. Methods such as PCA, t-SNE, or UMAP can decrease d, which can speed up nearest neighbor calculations. Another approach is to use approximate methods like locality-sensitive hashing (LSH) or specialized libraries that perform approximate searches, often good enough in practice and dramatically faster than the exact approach.

If exact nearest neighbor searches are still required, using a tree-based data structure like a KD-tree can speed up searches in moderate dimensions. However, in very high-dimensional spaces, these tree-based data structures can degrade to linear scan performance. There are also clever indexing approaches like the Annoy library (Approximate Nearest Neighbors Oh Yeah) and FAISS (Facebook AI Similarity Search) which can handle large amounts of data efficiently by using approximate searches.

Potential Follow-up Questions

Why is distance computation in high-dimensional spaces problematic?

When the dimension d grows very large, many distance metrics become less meaningful because distances between points start to concentrate, meaning the difference in distances between nearest and farthest points becomes small. This phenomenon is sometimes referred to as the "curse of dimensionality." It reduces the discriminative power of distance measures and makes K-NN less effective.

Additionally, tree-based indexing methods that rely on partitioning the space lose efficiency as d grows, leading to performance closer to a brute force linear search. Techniques like dimensionality reduction or approximate nearest neighbor methods are often required to mitigate these issues.

How would you implement approximate nearest neighbor search in practice?

One pragmatic way is to rely on libraries like FAISS (by Meta), Annoy (by Spotify), or ScaNN (by Google). These libraries implement specialized data structures that support sublinear or near-sublinear search times in practice. They typically achieve this by creating cluster-based indexes or using hashing-based approaches to group nearby points so that distance computations are constrained to only a subset of points.

A sample code snippet in Python using Annoy might look like:

from annoy import AnnoyIndex
import numpy as np

# Suppose we have data of dimension 100
dim = 100
t = AnnoyIndex(dim, 'euclidean')

# Build the Annoy index
for i in range(num_data_points):
    v = np.random.rand(dim)
    t.add_item(i, v.tolist())

t.build(10)  # 10 trees

# Query for nearest neighbors of a sample point
query_point = np.random.rand(dim).tolist()
neighbors = t.get_nns_by_vector(query_point, 5)  # get 5 nearest neighbors
print("Nearest neighbor indices:", neighbors)

This is much faster than performing a naive distance computation for each query.

Does the choice of distance metric impact performance for large datasets?

Yes, it can. Some distance metrics compute faster (like Manhattan distance which avoids square roots). However, the bigger issue is typically the scaling with N. Even if each distance computation is marginally faster, an O(N) approach may remain too slow for large datasets. The main speedup arises from data structures and indexing approaches that reduce the number of distance computations needed per query.

How does K-NN compare with parametric models on large datasets?

Parametric models (like linear/logistic regression, SVM with certain kernels, neural networks) usually learn a fixed set of parameters independent of N after training. Inference time for these models is often faster because inference relies on a function parameterized by a bounded set of weights or coefficients, rather than referencing all training samples. With K-NN, large datasets directly translate into large memory usage and slower query times, so parametric models can be more appealing for large datasets if they can maintain acceptable accuracy.

What are potential pitfalls when using KD-trees or Ball trees in high-dimensional data?

KD-trees and Ball trees are efficient in lower dimensions, where the number of divisions in the data structure is not too high relative to data dimension. As dimension increases, the partitions become less effective, leading the tree to degenerate. In high-dimensional scenarios, these trees offer little practical benefit compared to naive linear scans. The threshold where “high-dimensional” starts depends on factors like data distribution and the specifics of the dataset, but it can happen even at moderate dimensions such as a few tens.

How do you handle streaming data or real-time updates with K-NN?

A major downside of K-NN is that it can be costly to update if your dataset changes frequently. Each new data point might necessitate rebuilding or updating the entire structure (like a KD-tree or approximate index). Incremental approaches exist for some data structures (e.g. Annoy or Flann can be partially updated), but it can still be expensive. For truly real-time updates, parametric models that can be incrementally trained (like some online learning algorithms) may be more convenient.

How would you choose the value of K for a large dataset?

There is no single formula for choosing K; it is usually guided by cross-validation. The optimal K often increases with the number of data points. Smaller K can lead to noisier predictions, while larger K might smooth out the decision boundary too much. As the dataset grows, cross-validation remains the trusted approach to select K systematically. One also needs to keep in mind the increased computational cost when searching for more neighbors.

Does normalizing or standardizing features matter when using K-NN?

Yes, it can be critical because K-NN relies on a distance metric. If one feature has a much larger numerical range than others, it can dominate the distance calculation. Standardizing or normalizing features ensures that each dimension contributes roughly equally to the distance. This step becomes even more important for large, diverse datasets containing features on widely different scales.

What if the dataset is not only large but also imbalanced for classification?

When the dataset is imbalanced, the distance-based majority vote might become biased toward majority classes. One way to alleviate this is to weigh neighbors according to their distance or to resample the dataset. Another approach could be using a specialized metric, or weighting classes inversely proportional to their frequency.

How do you evaluate the efficiency of K-NN on large datasets?

You can monitor: • Inference time per query. • Memory usage for storing all points and indexing structures. • Scalability as data grows. • Accuracy metrics if approximate methods are used.

In practice, if queries are very frequent and the dataset is large, you might find that building a parametric or approximate neighbor approach yields better trade-offs.

Would you use K-NN for large datasets?

K-NN can be used, but not in its naive form unless the dataset is still within practical scale. Typically, you would consider approximate nearest neighbor methods or dimensionality reduction to mitigate K-NN’s computational and memory challenges. If those methods do not preserve accuracy or are still too slow, you might switch to a parametric or other non-parametric but more scalable model.

Below are additional follow-up questions

How do you handle concept drift in K-NN if the distribution changes over time?

When the data distribution changes (also called concept drift), the notion of “closeness” may shift significantly. If the model was trained on historical data that no longer reflects current conditions, nearest neighbors from the old distribution might not be representative of new points. An example is user behavior in an online system that changes seasonally or after a major event.

To handle concept drift, one approach is a sliding window that retains only the most recent data. Instead of maintaining all historical samples, you keep a buffer of the latest points (for instance, the last few million or thousand, depending on memory constraints). Then, you only perform K-NN queries on that recent buffer, ensuring the neighbors reflect the current distribution.

Another method is to use a weighting scheme that decreases the importance of older samples over time, so that new points have a higher influence on the final decision. In streaming contexts, incremental or online algorithms can adapt to new data as it arrives, though K-NN is typically more static and might need data structure rebuilds or partial updates to reflect the latest distribution.

Pitfalls: • If the data distribution changes rapidly and unpredictably, updating the nearest neighbor index can become frequent and expensive. • In non-stationary environments, ignoring older data too aggressively can cause the model to lose valuable contextual information, particularly if distribution periodically reverts to older patterns.

What is the role of interpretability in K-NN for large datasets?

K-NN is often considered interpretable in the sense that you can point to the neighbors that influenced a prediction (“these are the 5 neighbors that voted for this class”). This can be helpful for explaining certain predictions. However, for large datasets: • Storing and referencing all data points might be impractical for manual inspection. If each prediction is influenced by thousands or millions of data points, interpretability becomes less transparent. • If your data has high dimensionality, it can be difficult to visualize or intuitively understand why certain neighbors are close, diminishing the clarity of interpretation.

One might still attempt local explanations by sampling a smaller subset of relevant features or neighbors. Yet for truly huge datasets, interpretability often needs more specialized techniques (like local surrogate models or dimensionality reductions) to produce summaries of why specific neighbors are chosen.

Pitfalls: • Simply showing the nearest neighbors without summarizing their main distinguishing features might not be very enlightening for business stakeholders. • High dimensional spaces can have counterintuitive distance metrics, leading to misleading interpretations of neighbor proximity.

How can missing or incomplete features affect K-NN in large datasets?

K-NN relies on computing distances in a feature space, so missing or incomplete features can impede distance computations. If certain features are missing for some samples, you need a strategy: • Imputation: Fill missing values with means, medians, or model-based estimates. Large datasets allow you to train imputation models that can fill in missing values more reliably. • Distance definition: You might modify the distance metric to skip missing features, or to penalize them differently. Sometimes, a distance-based approach can automatically handle missing data if the distance function is carefully designed. • Removal of incomplete data: With very large datasets, you may remove rows having missing features if they are relatively rare. However, this might cause bias if the missingness is not random.

Pitfalls: • Imputation at scale can be computationally expensive if done naively. One must ensure it can handle large volumes of data. • Overly simplistic imputation (like replacing missing values with the mean) can distort the underlying feature distribution and degrade the distance measure.

Does K-NN scale well in a distributed computing environment?

K-NN can be parallelized to some extent by splitting the training data across multiple machines and performing partial distance computations in parallel. Each machine computes distances to its local portion of the dataset, and then results are aggregated (e.g., by merging partial neighbor lists).

However, you still must be able to distribute the dataset among workers, handle potential network overhead in sending partial neighbor results, and maintain consistent indexing structures. Approximate methods like FAISS also support distributed indexing, but the complexity of distributed synchronization can be significant.

Pitfalls: • Large-scale distributed K-NN might suffer from communication bottlenecks if each node has to send large amounts of distance computations or neighbor indices over the network. • Maintaining a global index or updating it frequently as data changes in a distributed environment can be tricky, especially if the system demands real-time queries.

When might random subsampling be beneficial for K-NN on extremely large datasets?

One strategy when dealing with extremely large datasets is to perform random subsampling to reduce the training set to a more manageable size. This can substantially reduce memory and computation costs at the expense of some accuracy. By sampling, you effectively approximate the overall distribution while limiting the data used during inference.

• Random sampling is straightforward to implement, but the choice of sample size matters. Too small a sample may degrade accuracy significantly, whereas too large undermines the purpose of sampling. • Stratified sampling can preserve class proportions, which is important in classification tasks to avoid skewing the neighbor distribution.

Pitfalls: • If there are rare classes or tail distributions, naive sampling might eliminate or underrepresent them. This can lead to poor performance for minority classes or outlier detection tasks. • Sampling might lose local structure if the data is very heterogeneous or has many subtle clusters.

What if we use weighted voting or distance-weighted K-NN for large datasets?

In the standard K-NN algorithm, each neighbor’s vote is typically weighted equally. Alternatively, one can give more weight to neighbors that are closer and less weight to those farther away. The distance-weighted approach can sometimes increase accuracy by reducing the influence of points that are near the boundary of the neighborhood.

For large datasets, distance weighting can help: • If data is dense, slight differences in distance might be significant. Weighting provides more fine-grained discrimination when multiple neighbors are close but not equally close. • It can mitigate the effect of an outlier neighbor if that neighbor is slightly farther than the “good” neighbors.

Pitfalls: • Distance-weighted voting still requires the same overhead of identifying the nearest neighbors. • If the dimension is large, small differences in distance might be lost in distance concentration effects, limiting how much benefit weighting can provide.

Can you use K-NN in an online or streaming manner without rebuilding an index each time?

K-NN is typically a lazy learner, meaning you store all data points and classify at query time. For an online or streaming scenario, new data points continuously arrive. If you maintain a data structure like a KD-tree or an approximate nearest neighbor index (Annoy, FAISS, etc.), you may need to rebuild or update this structure regularly.

Some structures (e.g. Annoy) support adding new items incrementally, but updates might still require partial re-indexing or building additional trees. For truly high-volume streams, maintaining a fully up-to-date index can be computationally intensive. The alternative is to let the index lag behind by a certain number of records or rely on a sliding window approach (dropping old data and adding new data in segments).

Pitfalls: • If the structure is not kept up-to-date, the neighbors might be stale and degrade prediction quality. • Continual insertion or deletion in large indexes can become a bottleneck, overshadowing any advantage in classification accuracy from K-NN.

How might you handle anomalies or outliers in a large dataset when using K-NN?

Outliers can distort neighbor-based predictions, especially if K is small. One approach is to perform outlier detection as a preprocessing step, removing or diminishing the influence of outliers. Alternatively, you can use robust distance measures (like median-based approaches) that reduce outlier impact.

In large datasets: • A few outliers may not significantly affect many queries if the data is densely clustered. However, they can still be an issue for queries in sparse regions. • Some advanced indexing structures have the option to exclude outliers or down-weight them during index building.

Pitfalls: • Outlier detection at scale might require additional passes over the data and can be time-consuming. • In some domains, what appears to be an outlier might actually contain essential signals (e.g., fraud detection). Automatically removing outliers could remove key patterns.

What trade-offs arise when combining dimensionality reduction with K-NN for large datasets?

Dimensionality reduction (e.g., PCA, autoencoders, UMAP) often speeds up neighbor searches by embedding the data in fewer dimensions. This can significantly reduce search times, but: • The reduced dimension might lose vital information, causing distances to be less accurate representations of true relationships in original feature space. • Non-linear dimensionality reductions can be computationally expensive for very large datasets, so you need to find a balance between feasible dimensionality reduction and speed gains in neighbor search.

Pitfalls: • Overly aggressive dimensionality reduction can collapse distinct classes or clusters, hurting performance. • If an embedding approach is misapplied or not tuned, you might introduce artifacts in the reduced space that degrade K-NN accuracy.