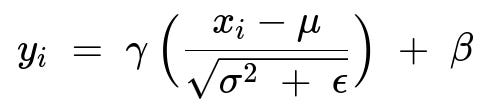ML Interview Q Series:How do Batch Normalization,Instance Normalization & Layer Normalization differ & can you describe any challenges that might arise when using Batch Normalization in deep networks?
📚 Browse the full ML Interview series here.
Comprehensive Explanation
Batch Normalization, Instance Normalization, and Layer Normalization are techniques designed to stabilize and accelerate the training of neural networks by normalizing intermediate activations. While they share a common theme of reducing internal covariate shift, they differ in how they compute the mean and variance, and this leads to variations in performance under different scenarios.
Underlying Formula for Normalization
They all rely on a similar transform, where the intermediate activation x_i (in plain text to avoid inline LaTeX) is normalized using mean and variance statistics, then scaled and shifted by trainable parameters gamma and beta. One can represent the core operation as:
Here, x_i is the activation for a given dimension i (depending on which axes are considered), mu is the mean over those chosen axes, sigma^2 is the variance over those chosen axes, epsilon is a small constant for numerical stability, gamma is a learnable scaling parameter, and beta is a learnable shifting parameter.
In each method, the difference lies in how mu and sigma^2 are computed:
Batch Normalization computes mu and sigma^2 across an entire batch of data for each feature channel.
Layer Normalization computes mu and sigma^2 across the features of a single sample.
Instance Normalization computes mu and sigma^2 across each channel in a single sample, typically used in tasks like style transfer.
Batch Normalization
This method calculates mean and variance across the batch dimension for each channel (in a convolutional network context) or feature (in a fully connected network context). Specifically, if you have a batch of size N, then for each feature channel, you compute the mean and variance over all N samples in the batch (plus spatial dimensions in CNNs). The normalized activations are then scaled and shifted.
Batch Normalization can dramatically speed up training and make networks less sensitive to initialization. It can, however, introduce some problems when batch size is very small or when the distribution of inputs to the network changes significantly between training and inference. Also, in certain architectures such as recurrent neural networks, it might be less effective unless applied with caution or replaced by alternative normalization layers.
Layer Normalization
Layer Normalization is applied across the features of each individual example. This approach is often used in recurrent or transformer-based architectures. By normalizing the entire set of features within a single example, Layer Normalization remains stable even when the batch size is small. It also ensures that each training sample is normalized independently of others, which can be particularly beneficial when training data are processed in non-i.i.d. ways or in tasks that deal with sequences.
Instance Normalization
Instance Normalization is similar to Layer Normalization, but in a convolutional setting, it normalizes across the spatial dimensions of each individual feature map within a single example. This is often used in style transfer tasks where the style representation is captured by the statistics of individual feature maps. Because each example’s channels are treated independently, Instance Normalization can remove certain style-specific features (e.g., illumination changes), making it popular in image generation tasks.
Potential Problems with Batch Normalization
When using Batch Normalization in deep neural networks, you can encounter:
Challenges with very small batch sizes. With extremely small batches, the estimated mean and variance for each batch may be unstable, leading to noisy updates.
Difficulty in matching training and inference statistics. During inference, fixed running estimates of mean and variance are used, which might be inaccurate if training batches are not representative or if the distribution changes.
Sensitivity in certain architectures. In recurrent networks, applying Batch Normalization can lead to less predictable behavior unless carefully designed. Alternatives like Layer Normalization or Group Normalization often work better in these cases.
Code Example in PyTorch
Below is a simple usage example in PyTorch. Batch Normalization is typically used right after a convolution (or fully connected) operation:
import torch
import torch.nn as nn
model = nn.Sequential(
nn.Conv2d(in_channels=3, out_channels=64, kernel_size=3, stride=1, padding=1),
nn.BatchNorm2d(64),
nn.ReLU()
)
To use Layer Normalization:
layer_norm_layer = nn.LayerNorm(normalized_shape=(64, 32, 32))
In the above snippet, (64, 32, 32) could be the shape of the convolutional layer’s output if it has 64 channels and a 32x32 spatial resolution.
Could you elaborate on situations where Layer Normalization outperforms Batch Normalization?
Layer Normalization often shines in sequence models or transformer architectures, where the batch size might be small or variable and the distribution of activations can change quickly over time. Because Layer Normalization normalizes across the features of a single example, it avoids the issue of computing statistics across the batch dimension. This makes training stable even if each batch has very few examples. It also allows the network to handle sequences of varying length more effectively, which is particularly useful in NLP tasks. In scenarios where you have large, consistent batch sizes, Batch Normalization might still be preferable due to its strong empirical performance in many vision tasks.
How does one handle the small batch size issue in practice when using Batch Normalization?
One strategy is to use a larger effective batch size through techniques like gradient accumulation, where gradients are accumulated over several mini-batches before performing an optimization step. Another method is to switch from Batch Normalization to a normalization approach that does not rely on the batch dimension, such as Layer Normalization or Group Normalization, especially when small batch sizes are unavoidable. Group Normalization is a compromise between Layer Normalization and Batch Normalization, where features are split into groups, and mean/variance are computed within each group.
When might Instance Normalization be more beneficial than other normalization techniques?
Instance Normalization is particularly useful in style transfer and artistic image generation tasks. In those applications, normalizing each feature map individually helps remove instance-specific contrast information while retaining structure. This manipulation of contrast across channels within an image is key to re-styling or re-coloring images. However, it might not always be beneficial for tasks requiring consistent, global understanding, such as classification on large and diverse datasets.
Are there performance implications of using Batch Normalization compared to Layer Normalization?
In many large-scale vision tasks with sufficiently large batches, Batch Normalization can deliver faster convergence and potentially better final performance due to the regularizing effect of using batch-level statistics. Layer Normalization, meanwhile, is more consistent across different batch sizes and is often preferred in NLP or whenever you want independence from the batch dimension. The computational cost of BN vs. LN is typically comparable, although BN can sometimes be optimized more heavily in certain deep learning frameworks due to its widespread usage.
What considerations should be made when using these normalizations in production?
When deploying models, the behavior of normalization layers can differ between training and inference modes. With Batch Normalization, one must ensure that running averages for mean and variance are properly updated during training and then used during inference. If these estimates are inaccurate, you can see a performance drop in production. Layer and Instance Normalization do not rely on batch-level running statistics, so they often have more predictable behavior in production, as normalization is consistently applied at each forward pass.
How would you summarize the key differences for real-world use?
While Batch Normalization is the default for many convolutional networks, it can struggle with small batches or non-vision tasks. Layer Normalization applies well to RNNs and Transformers, ensuring stable training across varying sequence lengths or batch sizes. Instance Normalization is invaluable in tasks like style transfer, focusing on per-image normalization of each feature map. The choice often depends on batch size constraints, dataset diversity, and the specific architecture.
Below are additional follow-up questions
How does Batch Normalization behave in large-scale distributed training, and what are the key considerations?
When training neural networks in a large distributed environment, each worker usually handles a portion of the training data. If Batch Normalization aggregates statistics at the local worker level rather than the global batch level, each worker may end up with different mean and variance estimates. This discrepancy can lead to instability during training or inconsistent updates of the running statistics, especially if some workers see very different data distributions.
One approach is to synchronize batch statistics across workers so that all workers share the same mean and variance. This involves additional communication overhead since the local mean and variance from each worker have to be combined at each step or mini-batch iteration. Another approach is to adopt techniques like Ghost Batch Normalization, where a large mini-batch is artificially formed by combining smaller sub-batches from each worker. However, this still demands efficient communication schemes to avoid a heavy slowdown. A mismatch between training-time statistics and inference-time statistics can arise if the distribution of data across different workers is not well balanced, which can degrade model performance significantly during inference.
A subtle challenge emerges when the global batch size is extremely large or extremely small. With a large global batch, the batch statistics become more stable, but the updates to model parameters might be less frequent. With a very small global batch, the fluctuation in the estimates can increase, possibly requiring modifications such as increasing the momentum used for running estimates or switching to a normalization method that is independent of batch size, like Layer Normalization or Group Normalization.
Are there particular pitfalls to watch for when using Batch Normalization with reduced-precision or quantized models?
In reduced-precision or quantized scenarios, numerical stability becomes even more critical. When using half-precision (FP16) or int-based quantization, the computation of mean and variance can suffer from rounding errors or overflow. This can produce inaccurate estimates of the batch statistics, thus making the normalization less stable. Moreover, in very deep networks, accumulated errors might become more pronounced layer by layer, especially if the variance values become too small or too large to be properly represented in a lower-precision format.
To address this issue, some frameworks implement a mixed-precision approach where certain calculations, like variance or mean, are kept in higher precision (FP32) even if the rest of the network runs in half-precision. Another strategy is to ensure that the batch size is large enough to reduce the per-sample variance in the mean and variance calculations. There might also be a need for carefully tuning the epsilon hyperparameter in the normalization formula, because in lower-precision regimes, even small numeric changes to epsilon can significantly impact stability.
What happens to Batch Normalization in the face of domain shifts or distribution changes over time?
Batch Normalization learns moving averages for mean and variance during training under the assumption that these statistics remain representative of the data seen at inference. If the underlying data distribution changes (commonly referred to as domain shift), the stored running averages become inaccurate. For instance, if a model trained on one domain is deployed on data with different lighting conditions, camera properties, or demographic attributes, the mismatch between training and deployment distribution can degrade model performance.
A typical mitigation strategy is to update the running statistics continuously during deployment, assuming you have access to unlabeled (or partially labeled) data in the new domain. This online adaptation can ensure that the BN layers reflect the new distribution. Alternatively, methods that are less dependent on batch-level statistics, such as Layer Normalization or Instance Normalization, can be more robust in situations where domain shifts are frequent or unpredictable. Another nuanced scenario arises if the distribution drifts slowly over time, making it unclear how frequently or aggressively to update the BN statistics.
Can you compare the advantages and disadvantages of Group Normalization relative to Batch and Layer Normalization?
Group Normalization splits the features into groups, computing the mean and variance for each group. It does not rely on the batch dimension, so it is more stable for small batch sizes compared to Batch Normalization. At the same time, it retains a level of feature grouping, which can outperform Layer Normalization in some vision tasks.
However, one must carefully choose the number of groups because grouping too few features can behave similarly to Instance Normalization, sometimes removing too much global context. Grouping too many features can approximate Layer Normalization or even revert to requiring large global batch statistics. Another subtlety is that Group Normalization might introduce slightly higher computational overhead compared to Batch Normalization in frameworks where BN kernels are heavily optimized. Additionally, the best choice of group size often depends on domain-specific factors like resolution and channel count, so there is typically an extra hyperparameter search overhead for finding an optimal configuration.
What considerations should be made if you freeze certain layers during transfer learning but keep Batch Normalization layers trainable?
In transfer learning, it is common to freeze a large portion of the network and only fine-tune the last few layers or a smaller subset of layers. If you freeze convolutional or dense layers but keep the Batch Normalization parameters trainable, a mismatch can occur. The running mean and variance might be updated based on activations that were originally calculated for a trained domain. By changing only partial layers, the data distribution at the BN layers can shift in unexpected ways.
If BN layers remain trainable while earlier layers are frozen, you might inadvertently change the statistics to reflect the new dataset’s distribution more accurately in the deeper layers. This could be beneficial, but it can also degrade performance if the newly learned BN statistics do not align well with the fixed representations from earlier layers. One possible strategy is to keep the BN parameters fixed as well, effectively using the original mean and variance. Alternatively, you can partially unfreeze earlier layers to allow them to adapt along with BN statistics, but that can require more computation and memory. Tuning the momentum parameter for the running estimates becomes crucial, as it governs how quickly these statistics adjust to the new domain.
In what ways can Batch Normalization affect the interpretability or visualization of feature activations?
Activations normalized by BN might mask certain signals that are otherwise visible when directly inspecting the raw distributions of neuron outputs. For instance, a neuron that used to produce high absolute values for specific data samples will have its range compressed after BN. This compression can make certain interpretability techniques, such as activation maximization or saliency maps, less straightforward to analyze.
Moreover, changes in BN parameters (gamma and beta) can make it harder to attribute changes in the output to specific neurons or layers, as these parameters effectively rescale and shift all activations at once. While BN helps in training stability and speed, it modifies how we interpret raw activation magnitudes. A recommended practice is to consider the pre-BN or unnormalized output if you aim to visualize raw channel responses. Another strategy is to disable BN (setting gamma to 1, beta to 0) at inference when generating visual explanations, though that can also alter the model’s performance. This trade-off means interpretability is often not as direct in BN-based architectures as in networks without normalization.
Does Batch Normalization behave differently in generative models compared to discriminative models?
In generative models, particularly Variational Autoencoders (VAEs) or Generative Adversarial Networks (GANs), the distribution of generated samples and the generator’s internal activations can change rapidly during training. Batch Normalization in the generator can introduce correlation among samples within the same batch, potentially leading to artifacts, especially if the batch statistics dominate. In some GAN variants, instance-level normalization or adaptive instance normalization is used to fine-tune style-related features without forcing correlation across a batch.
An additional pitfall is mode collapse in GANs, which can be exacerbated or alleviated depending on how BN is configured. If the batch size is small, then the BN statistics for the generator may not be stable, causing training dynamics to oscillate. Another subtlety is that the discriminator and generator often have competing objectives; BN might help one sub-network train more smoothly, but this can unbalance the adversarial training if the other network struggles to maintain consistent statistics. Consequently, many successful GAN architectures either do not rely heavily on BN or carefully tune it in combination with other normalization layers (e.g., instance or pixel normalization) to achieve stable training.