Not All LLM Reasoners Are Created Equal
LLMs still has a long way to get good at Math
LLMs still has a long way to get good at Math
This @GoogleDeepMind and @Microsoft paper shows, LLMs show strong performance on individual math problems but struggle with chained problems where the answer to one informs the next, raising questions about their true reasoning abilities.
Techniques in this Paper 🧠:
• Created Compositional GSM dataset: Pairs of grade-school math problems
• Q1 answer needed for Q2 solution
• Evaluated LLMs on individual problems and combined pairs
• Compared combined accuracy with expected individual accuracy
• Tested various models: Gemini series, GPT-4o, Llama 3, specialized math models, etc.
Key Insights from this Paper 💡:
• LLMs struggle with multi-hop reasoning, leading to a "reasoning gap"
• Reasoning gap might stem from distraction and excessive context
• Larger LLMs generally outperform smaller, specialized models
• Fine-tuning on grade-school math can lead to overfitting
• Instruction tuning and code generation improvements vary by model size
• High scores on standard benchmarks don't reflect true multi-step reasoning abilities
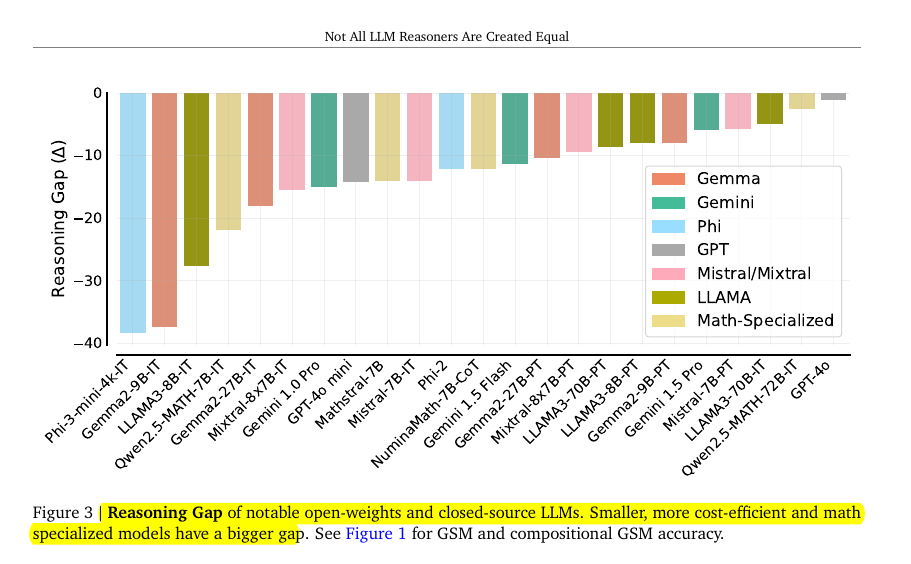
Results 📊:
• Reasoning gap (Δ): 30-40% for smaller models, 1-5% for frontier LLMs
• Larger models (e.g., Gemini 1.5 Pro, GPT-4o) show smaller reasoning gaps
• Specialized math models (e.g., Mathstral-7B, NuminaMath-7B-CoT) exhibit larger gaps
• Fine-tuning: Performance on Compositional GSM drops after 100 steps while GSM8K improves
• Code generation: Improves Compositional GSM accuracy by 69-149% for smaller models
LLMs excel at individual math problems but falter on chained tasks, revealing limitations in multi-step reasoning.
Reasoning Gap: Most models demonstrate a noticeable gap between their reasoning performance on GSM8K and compositional GSM, in which pairs of GSM8K test questions are chained together so that the answer of the first question (Q1 ) is a variable in the second one (Q 2). The model is required to correctly answer both questions to solve the problem.