One Initialization to Rule them All: Fine-tuning via Explained Variance Adaptation
Explained Variance Adaptation (EVA) improves LoRA by letting data guide weight initialization and rank distribution across layers.
Explained Variance Adaptation (EVA) improves LoRA by letting data guide weight initialization and rank distribution across layers.
LoRA + Smart Data Analysis = EVA: Like giving your model a data-driven compass.
So EVA helps LoRA work smarter, not harder, by studying the data first
Original Problem 🔍:
Parameter-efficient fine-tuning methods like LoRA lack data-driven initialization and adaptive rank allocation, leading to suboptimal performance on downstream tasks.
Solution in this Paper 🛠️:
• Explained Variance Adaptation (EVA) method proposed
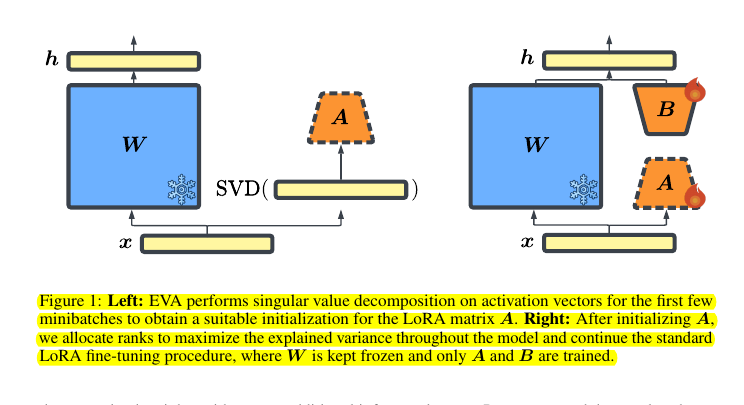
• Performs SVD on minibatches of activation vectors for data-driven initialization
• Redistributes ranks across model layers to maximize explained variance
• Combines advantages of data-driven initialization and adaptive ranks
Key Insights from this Paper 💡:
• Data-driven initialization leads to more effective fine-tuning
• Adaptive rank allocation improves performance over uniform ranks
• Combining EVA with other LoRA variants further boosts results
• EVA is particularly effective for in-domain tasks
Results 📊:
• EVA consistently achieves highest average performance across tasks
• Language generation: Highest scores on math and reasoning tasks
• Language understanding: Improves average performance on GLUE benchmark
• Image classification: Highest average score on 19 diverse VTAB-1K tasks
• Reinforcement learning: Exceeds LoRA and full fine-tuning performance
👉 The main innovations of Explained Variance Adaptation (EVA) are:
Data-driven initialization: It initializes LoRA weights by performing singular value decomposition (SVD) on minibatches of activation vectors from the downstream task data.
Adaptive rank allocation: It redistributes ranks across model layers to maximize explained variance, rather than using a uniform rank distribution.
👉 Key steps of the EVA method:
Compute SVD on activation vectors for minibatches of downstream data
Initialize LoRA matrix A with top singular vectors
Redistribute ranks across layers based on explained variance
Continue with standard LoRA fine-tuning