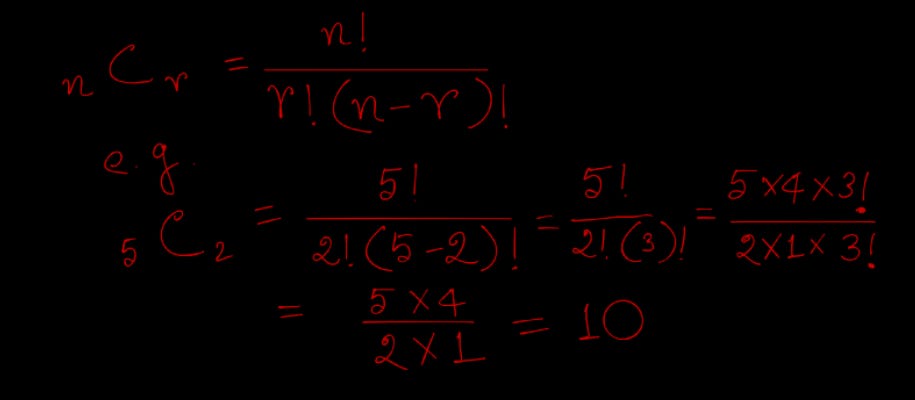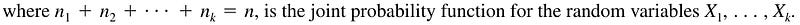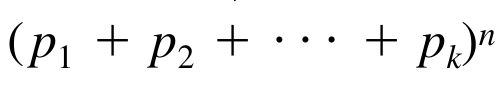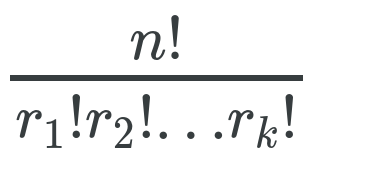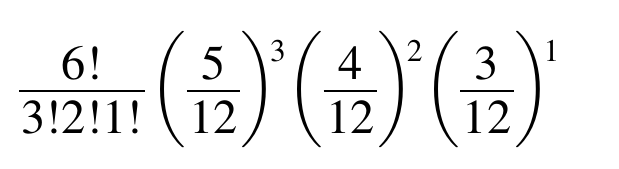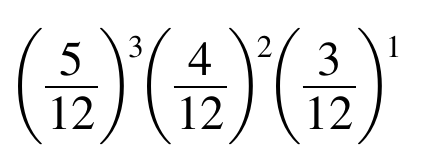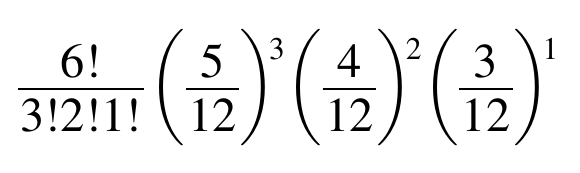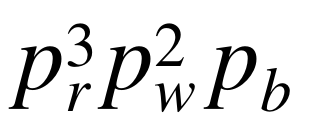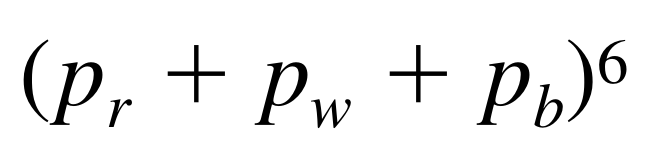Probability Problem-Solution series for Data Science -Part-1

First some fundamental formulas

First some fundamental formulas

The combination of n different things taken r at a time is denoted by nCr and used the formula for calculation is below

If two dice are rolled, what is the probability that the sum of the upturned faces will equal 7?

Solution — We shall solve this problem under the assumption that all of the 36 possible outcomes are equally likely. Since there are 6 possible outcomes-namely, (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), and (6, 1)-that result in the sum of the dice being equal to 7, the desired probability is 6/36 = 1/6

Problem -1 asked at a Google Interview:

If the probability of seeing a car on the highway in 30 minutes is 0.95, what is the probability of seeing a car on the highway in 10 minutes? (assume a constant default probability)

Some clarifications that can help are:

“Seeing a car” means “seeing at least 1 car.”

“Constant default probability” basically means there is a constant probability rate of seeing a car (there’s no picking of probability during rush hour traffic, for example). Mathematically this can be stated as —Probability of observing a car in any given non-overlapping time interval of equal length are equal and independent.

With this assumption, I can think of the probability of seeing a car during a time interval is like a coin flip event, which also occurs with “Constant default probability”

So, now, think about each 10-minute interval like a coin flip. Suppose the probability of not seeing a car in 10 minutes is p.

Now first recount the Probability Multiplication Rules

The multiplication rule is about the probability of two events happening at the same time. There are two multiplication rules. The general multiplication rule formula is:

P(A ∩ B) = P(A) * P(B|A)

means “the probability of A happening given that B has occurred”.

If the two events are independent. In other words, it only works if one event does not change the probability of the other event then,

P(A and B) = P(A) * P(B)

Let’s divide 30 minutes time intervals into three 10 minutes intervals as A, B, and C.

P(not A) = Probability of not seeing a car in the first 10 minutes

P(not B) = Probability of not seeing a car in the second 10 minutes

P(not C) = Probability of not seeing a car in the third 10 minutes

As all are independent events with constant default Probability, so

P(not A) = P(not B) = P(not C) = lets say p

Then what is the probability of not seeing a car in 20 minutes? This is the probability of not seeing a car in 10 minutes, followed by the same event.

Pr(no cars in 20) = Pr(no cars in 10) Pr(no cars in 10)

= p * p = p²

Similarly, the probability of not seeing a car in 30 minutes is the probability of not seeing a car in 20 minutes, followed by the event of not seeing a car in another 10 minutes.

Pr(no cars in 30) = Pr(no cars in 20) Pr(no cars in 10) = p² * p = p³

Now the probability of seeing at least 1 car in 30 minutes can be calculated as the complement event, equal to 1 minus the probability of seeing no cars in 30 minutes.

Pr(at least 1 car in 30) = 1 — Pr(no cars in 30) Pr(at least 1 car in 30) = 1 — p³

We are given this is equal to 0.95. We can solve for p:

1 — p³ = 0.95 p³ = 0.05 p = (0.05)^1/3 ≈ 0.368

This is the probability of seeing no cars in 10 minutes. The probability of seeing at least 1 car is the complement event, equal to 1 minus the probability of seeing no cars in 10 minutes.

Pr(at least 1car in 10) = 1 — Pr(no cars in 10) Pr(at least 1 car in 10) = 1 — p Pr(at least 1 car in 10) ≈ 0.632

So the final answer — the probability of seeing at least 1 car on the highway in 10 minutes is approximately 63 percent.

Probability Problem-2

First the formulae of The Multinomial Distribution

This distribution, which is a generalization of the binomial distribution, is called the multinomial distribution since the above equation is the general term in the multinomial expansion of

---

Probability Problem-3

A box contains 5 red balls, 4 white balls, and 3 blue balls. A ball is selected at random from the box, its color is noted, and then the ball is replaced. Find the probability that out of 6 balls selected in this manner, 3 are red, 2 are white, and 1 is blue

Method 1 (by formula):

Lets first calculate the total Probabilities of choosing a colored ball out of Total 12

P(Total prob of red at any drawing) => 5 / 12

P(Total prob of white at any drawing) => 4/12

P(Total prob of blue at any drawing) => 3/12

Now the formulae we are going to apply is that of Finding the Number of Permutations of n Non-Distinct Objects which is

And also the by the Multiplication theorem of probability / Formula for Joint Probability

If A and B are independent events, we can reduce the formula to

P(A and B) = P(A) * P(B)

This means the probability of choosing any red ball is 5 / 12. Then the probability of choosing 3 red balls is (5 /12)^3

So, then the required probability for our problem is

---

Explanations

The probability of choosing any red ball is 5 /12. Then the probability of choosing 3 red balls is (5 /12)^3. Similarly, the probability of choosing 2 white balls is (4/ 12)^ 2, and of choosing 1 blue ball, (3 12)^1.

And therefore, the probability of choosing 3 red, 2 white, and 1 blue in that order is

But the same selection can be achieved in various other orders, and the number of these different ways is

Then the required probability is

Method 2 (by the law of multinomial expansion) :

The required probability is the term

in the multinomial expansion of

where

p_r = 5 /12,

p_w =4/ 12, and

p_b =3/12.

By actual expansion, the above result is obtained.