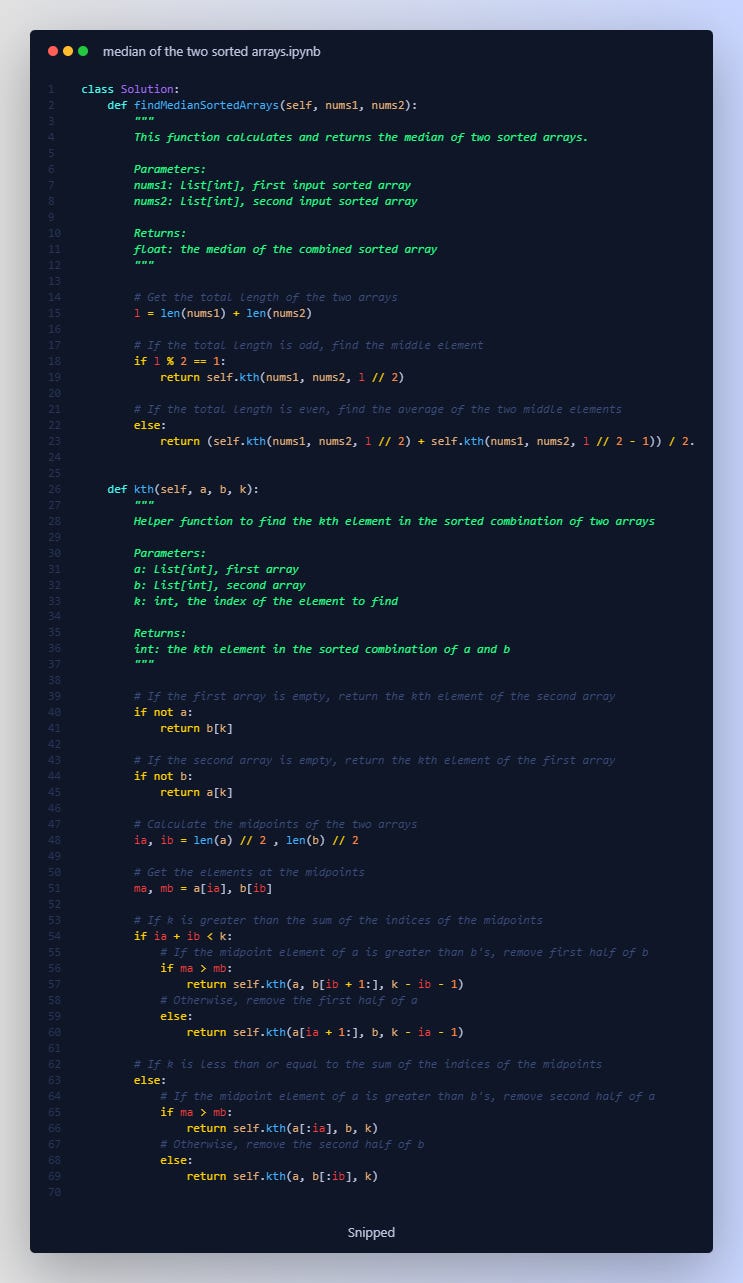
Python Interview Problem (famous in Leetcode) - Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays

🚀 Great Python Interview Problem (famous in Leetcode) - Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays 🚀🚀

And its in the 'HARD' Category of Leetcode

The overall run time complexity should be O(log (m+n)).

Example 1 of how the function should work:

Input: nums1 = [1,3], nums2 = [2]

Output: 2.00000

Explanation: merged array = [1,2,3] and median is 2.

Example 2 of how the function should work:

Input: nums1 = [1,2], nums2 = [3,4]

Output: 2.50000

Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.

-----------------------

The solution here is an implementation of a divide and conquer approach to find the median of two sorted Barrays. It uses the concept of binary search in an innovative way.

**Step-by-step Explanation**

1. 👉 **findMedianSortedArrays Function**: It starts by calculating the total length of the combined array and then, it checks if this total length is odd or even.

   - If the length `l` is odd, it implies the combined sorted array will have a single middle element, and that will be the median. In this case, it calls the helper function `kth` with `l // 2` as the value of `k` (since `k` is zero-based indexed, `l // 2` will point to the middle element).

   - If the length `l` is even, it implies the combined sorted array will have two middle elements, and the median will be the average of these two. In this case, it calls the `kth` function twice with `l // 2` and `l // 2 - 1` as the values of `k`, and calculates the average of the returned results.

2. 👉 **kth Function**: This is a helper function which is used to find the kth element of two sorted arrays `a` and `b`.

   - If array `a` is empty, it returns the kth element of array `b` (as all elements in `b` are guaranteed to be larger).

   - If array `b` is empty, it returns the kth element of array `a` (for the same reason).

   - It then calculates the indices `ia` and `ib` as the midpoints of `a` and `b`, and `ma` and `mb` as the elements at these midpoints.

   - The key insight is that if `ia + ib < k`, the kth element must be located in the second half of `a` or `b`. If `ma > mb`, it must be in the second half of `b`, otherwise, it's in the second half of `a`. Hence it discards the first half of the appropriate array and repeats the process.

   - If `ia + ib >= k`, the kth element must be located in the first half of `a` or `b`. If `ma > mb`, it must be in the first half of `a`, otherwise, it's in the first half of `b`. Hence it discards the second half of the appropriate array and repeats the process.

-------------------

👉 Explanation of the below block from the above solution

```py

 if ia + ib < k:

            # If the midpoint element of a is greater than b's, remove first half of b

            if ma > mb:

                return self.kth(a, b[ib + 1:], k - ib - 1)

            # Otherwise, remove the first half of a

            else:

                return self.kth(a[ia + 1:], b, k - ia - 1)

```

This portion of the code operates based on the principle of binary search and exploits the property of the sorted arrays.

The expression `ia + ib < k` is checking if the combined length of the two halves of `a` and `b` (i.e., up to their median indices) is less than `k`. If so, this means that the `kth` element we are searching for falls in the second half of either array `a` or array `b`.

The reason for this is as follows: If `ia + ib` is less than `k`, then the `kth` element of the combined array lies beyond the midpoint of both arrays `a` and `b`.

Let's say we have two sorted arrays `a` and `b`, and we are looking for the 5th element of the combined sorted array. For example:

```py

a = [1, 3, 8]  # length is 3, so midpoint index is 1 (0-based index)

b = [2, 7, 9, 10, 11]  # length is 5, so midpoint index is 2

```

If `k = 5`, the sum of the midpoint indices `ia + ib` is 3, which is less than `k`. Therefore, we know that the `kth` element (in this case, the 5th element) must be in the second half of either `a` or `b`.

The subsequent if-else block within this then decides which array's first half to discard. It compares the median elements `ma` and `mb` of arrays `a` and `b`, respectively.

- If `ma > mb`, we can safely eliminate the first half of `b` (i.e., all elements up to the median of `b`), because they cannot be the `kth` element. This is because they are all less than or equal to `mb`, and `mb` is less than `ma` (and thus also less than all elements in the second half of `a`). Since we have removed some elements from `b`, we also decrease `k` by the number of elements we've removed (`ib + 1`) to reflect this change.

- If `ma <= mb`, we eliminate the first half of `a`, for similar reasons. All elements in the first half of `a` are less than or equal to `ma`, which is less than or equal to `mb` (and thus also less than all elements in the second half of `b`). We decrease `k` by the number of elements we've removed (`ia + 1`).

In either case, we perform a new call to `kth`, but with a smaller array and a correspondingly reduced `k`.

By iteratively applying this process, we can find the `kth` element of the combined array in logarithmic time, as each step approximately halves the size of the search space.

-------------------

👉 **Time Complexity**:

The solution algorithm here follows a binary search type pattern, with each step discarding about half of one of the arrays.

Therefore, the time complexity is O(log(min(m,n))) where `m` and `n` are the sizes of the input arrays.

The complexity is not O(log(m+n)) because in each step we discard about half of one of the arrays, and the smaller array is the limiting factor.

👉 **Space Complexity**:

Since the problem is solved using recursion, the space complexity of the solution will be O(log(min(m,n))) due to the space required for the recursion stack. Each recursive call reduces the size of the problem and hence the depth of the recursion tree will be logarithmic to the size of the smaller array.

👉 **Potential Bottlenecks & Edge Cases**:

1. **Recursive Depth**: If one of the arrays is significantly larger than the other, and the smaller array doesn't get reduced in the initial steps, the recursive stack depth might become quite large. In extreme cases, this might lead to a `RecursionError` or a stack overflow.

2. **Duplicate Elements**: The code should handle arrays with duplicate elements correctly, as it always moves to the next index (ignoring the current index) in the second half of the search space. If duplicate medians are present, it will still find the correct median.

3. **Empty Arrays**: If both the arrays are empty, the code will throw an error as there will be no median element. This edge case should be handled separately before making the first call to the `kth` function.

4. **Large Arrays**: If the input arrays are very large, the code could become slow. However, the binary search pattern should generally ensure good performance.