Python Interview Problem - Given an integer n, return true if and only if it is an Armstrong number

👉 The Problem

First, what is an Armstrong number?

The k-digit number n is an Armstrong number if and only if the kth power of each digit sums to n.

➡️ Example 1:

Input: n = 153

Output: true

Explanation: 153 is a 3-digit number, and 153 = 1^3 + 5^3 + 3^3.

➡️ Example 2:

Input: n = 123

Output: false

Explanation: 123 is a 3-digit number, and 123 != 1^3 + 2^3 + 3^3 = 36.

-----------

👉 The solution

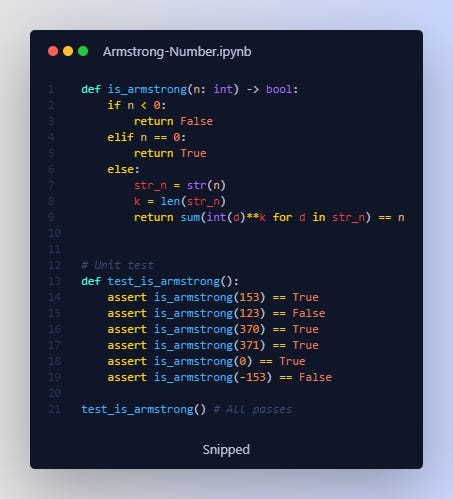
The idea is simple: we convert the integer into a string to get the number of digits, and then iterate over each digit, take it to the power of the number of digits, and sum all these. We check if this sum is equal to the original number.

------------

👉 Explanation of the Solution:

First, we convert the input number n to a string, str_n. This allows us to easily count the number of digits k in the number using the len() function.

We then create a generator expression int(d)**k for d in str_n which takes each digit d in str_n, converts it back to an integer, raises it to the power k (the number of digits), and sums all these results. This is done using the sum() function.

Finally, we compare this sum to the original number n. If they're equal, n is an Armstrong number and the function returns True; otherwise, it returns False.

----------

👉 Time Complexity:

The time complexity of the code is O(k), where k is the number of digits in the input number. This is because we are iterating over each digit once. The operations inside the loop (raising to the power and summing) are all constant time, so the overall time complexity is linear in the number of digits.

👉 Space Complexity:

The space complexity is O(k), where k is the number of digits in the number. This is because when we convert the integer to a string, it needs to allocate memory space to store the string.

👉 Potential Bottlenecks:

The potential bottleneck in Python could be very large numbers, since the time and space complexity increase with the number of digits, and Python might take significant time and memory to process them.

------------------

Further question on Armstrong Number - If we asked to output all Armstrong number below a certain no, what is a better way to do it, running loop upto given no or generating few random no and doing much less iterations

If we're asked to output all Armstrong numbers below a certain number, the more efficient way would be to run a loop up to the given number. The reason being, Armstrong numbers have specific properties and are not randomly distributed, so we can't just generate random numbers and check them. Also, there's no known closed-form Math formula for generating all Armstrong numbers below a certain number, so we can't avoid checking all numbers.

Below Python code to solve the problem:

The time complexity is O(n*k), where n is the limit and k is the number of digits in the number. This is because we need to iterate over all numbers from 0 to `limit - 1`, and for each number, we need to iterate over its digits. The space complexity is O(m), where m is the number of Armstrong numbers below the limit. This is the space required to store the output.

-----------------------

If you enjoyed this post:

1. Follow me @rohanpaul_ai on Twitter for more of these every day and

2. Also, check out my MachineLearning YouTube channel