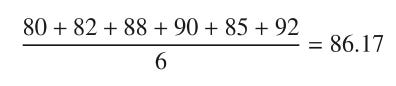What K-Fold Cross Validation really is in Machine Learning in simple terms
The basics of cross validation are as follows: the model is trained on a training set and then evaluated once per validation set. Then the evaluations are averaged out. This method provides higher accuracy. However, because the training time is multiplied by the number of validation sets, this is more computationally expensive.
My YouTube video explaining the exact steps of k-fold Cross-Validation
To start with some popular types of Cross Validation techniques are:
K-fold cross-validation
Stratified K-fold cross-validation
Hold-out based cross-validation
Leave-one-out cross-validation
Group K-fold cross-validation
Out of these, in this post I will ONLY discuss k-fold cross validation.
To help the machine learning algorithm estimate what its performance will be on the never-before-seen examples (the test set), it is best practice to further split the training set into a training set and a validation set.
For example, if we split the training set into fifths, we can train on four-fifths of the original training set and evalulate the newly training model by making predictions on the fifth slice of the original training set, known as the validation set.
It is possible to train and evaluate like this five times — leaving aside a different fifth slice as the validation set each time. This is known as k-fold cross-validation, where k in this case is five. With this approach, we will have not one estimate but five estimates for the generalization error.
We will store the training score and the cross-validation score for each of the five runs, and we will store the cross-validation predictions each time. After all five runs are complete, we will have cross-validation predictions for the entire dataset. This will be the best all-in estimate of the performance the test set.
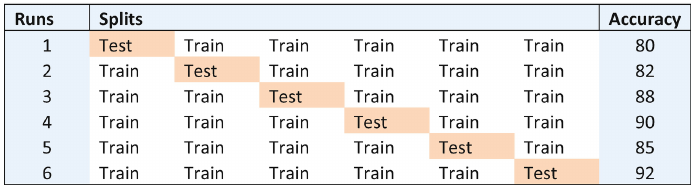
An example of k-fold cross-validation is depicted in below figure, where k = 6.
This six-fold cross-validation has its data split into six chunks, one reserved for testing and the remaining five data folds reserved for training. The accuracy column shows a variation of accuracy between 80% to 92%. The average accuracy is given by
Cross-validation can be run for different algorithms for different ranges for the same dataset. Depending on which algorithm offers an acceptable range of accuracy, that algorithm can be chosen as optimal for a given dataset. In summary, cross-validation is not generally used to find the best performing model. It is used more to validate or understand a particular model’s performance for a given dataset and new test data. The general approach in real life is to tune a model by measuring it while varying it with different parameters.
The advantages of cross-validation are that it is useful to systematically test a new model with data, and it can identify models with high-variance or over-fitting issues.
Drawback of K-Fold Cross Validation
Essentially its a computational issue because each of the split need to be trained k-times. If it takes too long to train, you use single split of data (eg enormous Neural networks). Equally if its too long because you have so much data, then a single split will still be reliable.