Your Mixture-of-Experts LLM Is Secretly an Embedding Model For Free
MoE models secretly contain powerful embedding capabilities within their routing mechanisms.
MoE models secretly contain powerful embedding capabilities within their routing mechanisms.
→ Router weights in MoE models capture semantic meaning better than traditional embeddings
→ Unlock better embeddings by tapping into how MoE models route between experts
Original Problem 🔍:
LLMs excel in generation tasks but struggle as embedding models without finetuning, limiting their versatility.
Solution in this Paper 🧠:
• Proposes MoE Embedding (MoEE) combining routing weights (RW) from MoE LLMs with hidden state (HS) embedding
• Explores two combination strategies: MoEE (concat) and MoEE (sum)
• Leverages complementary nature of RW (input-sensitive) and HS (output-dependent)
• Utilizes pre-trained MoE LLMs without additional training
Key Insights from this Paper 💡:
• MoE routers serve as off-the-shelf embedding models
• RW captures high-level semantics and is more robust to prompt variations
• Combining RW and HS provides comprehensive input representation
• MoEE improves performance on embedding-focused tasks without finetuning
Results 📊:
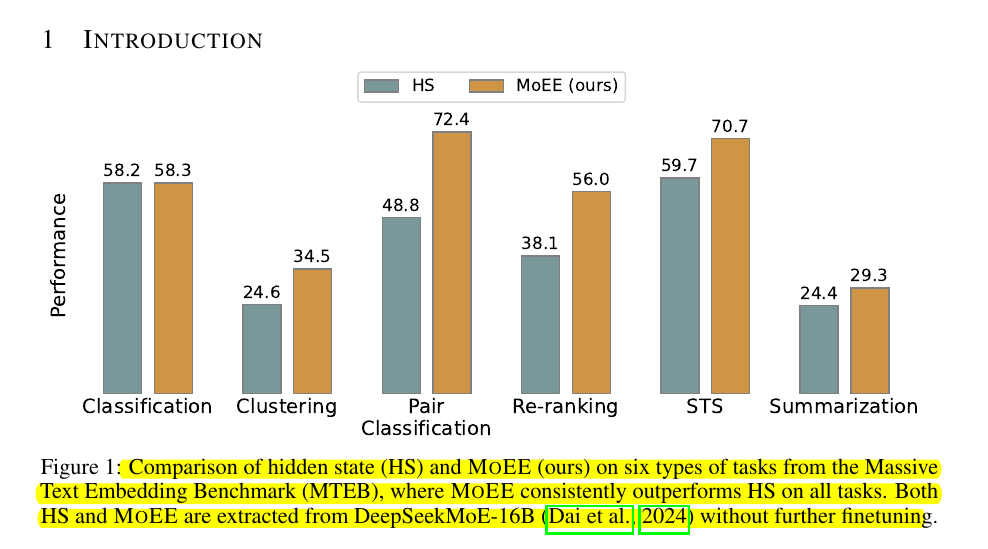
• MoEE consistently outperforms standalone RW and HS across MTEB tasks
• MoEE (sum) achieves best results, balancing input and output information
• Significant gains in semantic textual similarity, classification, and clustering
• DeepSeekMoE-16B: 22.45% improvement from HS (35.36) to MoEE (sum) (43.30)
• With PromptEOL: 25.96% improvement for DeepSeekMoE-16B
🔎 The robustness of routing weights (RW) embeddings compared to hidden state (HS) embeddings
The research shows that RW embeddings are more robust to the choice of prompts compared to HS embeddings. RW demonstrates greater stability and consistently lower variance across different prompts, making it a more reliable option for tasks where prompt variability is expected.
🛠️ The methods proposed for combining RW and HS embeddings in MoEE
The paper explores two main combination strategies:
MoEE (concat): Simple concatenation of RW and HS embeddings.
MoEE (sum): A weighted sum of the similarities computed separately on RW and HS. The study finds that MoEE (sum) often achieves the best results, as it allows for balancing output-dependent information with input-sensitive features.